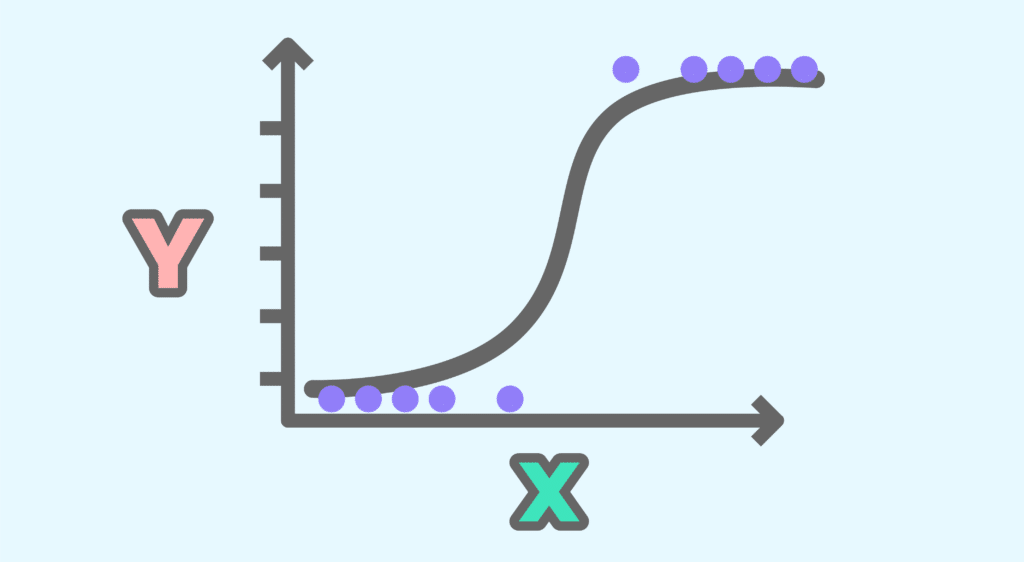
Wenn Du Dich für Machine Learning und Klassifizierungsprobleme interessierst, hast Du sicher schon einmal das logistische Regressionsmodell kennengelernt. Und das aus gutem Grund! Es ist eines der einfachsten und am besten interpretierbaren Modelle für Machine Learning, das sowohl kontinuierliche als auch diskrete Daten verarbeiten kann. Die damit erzielten Ergebnisse sind alles andere als lächerlich.
Was verbirgt sich denn hinter dieser Wundermethode? Und noch wichtiger: Wie kann sie für Python verwendet werden? Die Antwort in diesem Artikel.
Definition
Logistische Regression ist ein statistisches Modell zur Untersuchung der Beziehungen zwischen einer Reihe von qualitativen Variablen Xi und einer qualitativen Variable Y. Es handelt sich um verallgemeinerte lineare Modelle (VLM) mit einer logistischen Funktion als Kopplungsfunktion.
Ein logistisches Regressionsmodell kann auch die Wahrscheinlichkeit vorhersagen, dass ein Ereignis eintritt (Wert 1) oder nicht eintritt (Wert 0), und zwar auf der Grundlage der Optimierung der Regressionskoeffizienten. Dieses Ergebnis schwankt immer zwischen 0 und 1. Liegt der vorhergesagte Wert über einem Schwellenwert, ist das Ereignis wahrscheinlich; liegt der Wert unter demselben Schwellenwert, ist es unwahrscheinlich.
Auch interessant:
- 4 Arten von Statistik Bias, die jeder kennen sollte
- Open CV – Alles über Computer Vision
- Flask – Der bekannteste Python Framework
- NFT – Was das ist und wie du damit reich werden kannst
Wie wird dies mathematisch übersetzt/geschrieben?
Betrachten wir eine Eingabe X= x1 x2 x3 … xn , so zielt die logistische Regression darauf ab, eine Funktion h zu finden, die wir berechnen können:
y= {1 si hX≥ Schwellenwert, 0 wenn hX< Schwellenwert}
Wir gehen also davon aus, dass unsere Funktion h eine Wahrscheinlichkeit zwischen 0 und 1 ist, parametrisiert durch =1 2 3 n, die zu optimieren sind, und dass der von uns definierte Schwellenwert unserem Klassifizierungskriterium entspricht — in der Regel ist der Wert 0,5.
Die Funktion, die diese Bedingungen am besten erfüllt, ist die Sigmoidfunktion, die auf R mit Werten in [0,1] definiert ist. Sie ist wie folgt geschrieben:
Grafisch entspricht sie einer S-förmigen Kurve, deren Grenzen 0 und 1 sind, wenn x nach -∞ bzw. +∞ tendiert, und die bei x = 0 durch y = 0,5 verläuft.
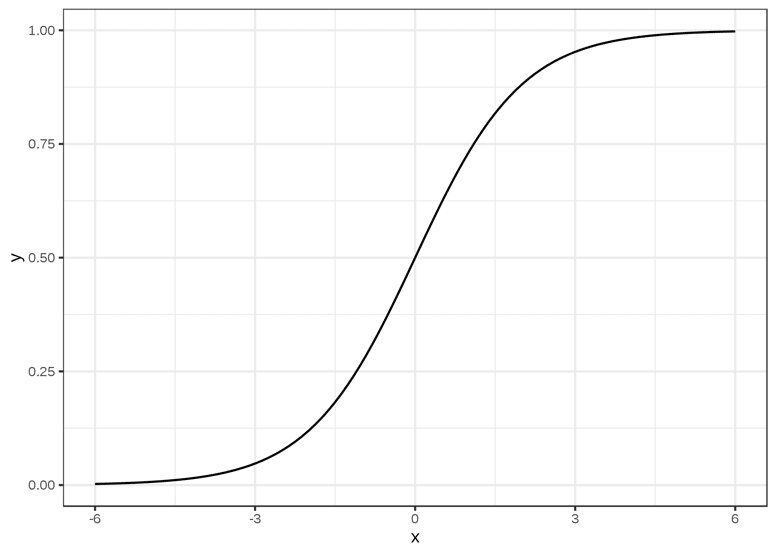
Und was ist mit unserer Klassifizierung?
Die Funktion h, die die logistische Regression definiert, wird so geschrieben:
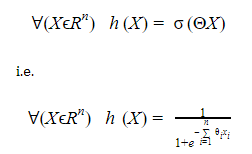
Das Problem der Klassifizierung durch logistische Regression stellt sich dann als ein einfaches Optimierungsproblem dar, bei dem wir bei gegebenen Daten versuchen, den besten Parametersatz Θ zu erhalten, mit dem unsere Sigmoidkurve am besten zu den Daten passt. Hier kommt unser maschinelles Lernen ins Spiel.
Sobald dieser Schritt abgeschlossen ist, können wir uns einen Überblick über das Ergebnis verschaffen:
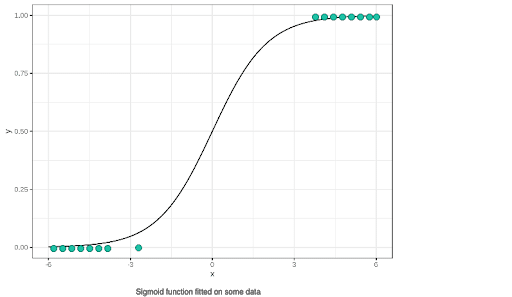
Nach der Festlegung des Schwellenwerts müssen nur noch die Punkte entsprechend ihrer Position in Bezug auf die Regression klassifiziert werden. So ist die Klassifizierung abgeschlossen!
Logistische Regression: Praxis
In Python ist es ganz einfach: Wir verwenden die Klasse LogisticRegression des Moduls sklearn.linear_model als normalen Klassifikator und trainieren ihn auf bereits bereinigten und in Trainings- und Testdatensätze aufgeteilten Daten – das war’s!
Auf der Ebene des Codes gibt es nichts einfacheres:
Für fortgeschrittene Anwendungsfälle bietet sich ein Kurs an, der vom Datascientest-Team geleitet wird. Mach mit!
Logistische Regression in der Datenwissenschaft
In der Datenwissenschaft wird logistische Regression verwendet, um die Wahrscheinlichkeit oder die Chance zu prognostizieren, dass ein Ereignis eintritt oder nicht, basierend auf den Werten von mehreren unabhängigen Variablen.
Sie eignet sich besonders gut für binäre Klassifikationsprobleme, bei denen es darum geht, ob ein Ereignis in eine von zwei Kategorien fällt, wie zum Beispiel „Ja“ oder „Nein“, „Erfolg“ oder „Misserfolg“, „Kauf“ oder „Nicht-Kauf“.
Der Algorithmus verwendet historische Daten, um eine mathematische Funktion zu erlernen, die die Beziehung zwischen den unabhängigen Variablen und der Zielvariable, also dem Ereignis, das prognostiziert werden soll, beschreibt.
Diese Funktion wird dann verwendet, um Vorhersagen für neue Daten zu treffen. Logistische Regression ist einfach zu implementieren und zu interpretieren, und sie ermöglicht es Dir, die Auswirkungen einzelner Variablen auf das Vorhersageergebnis zu analysieren.
Eine der Hauptanwendungen von logistischer Regression in der Datenwissenschaft ist die Vorhersage von Wahrscheinlichkeiten für Kundenverhalten, wie zum Beispiel ob ein Kunde ein Produkt kaufen wird oder nicht. Es wird auch in vielen anderen Bereichen wie medizinischer Diagnostik, Betrugsprävention, Marktforschung und vielen anderen angewendet.
Es ist wichtig zu beachten, dass logistische Regression auch ihre Einschränkungen hat und nicht für alle Arten von Daten und Problemstellungen geeignet ist. Es ist daher wichtig, die Vor- und Nachteile dieser Methode sorgfältig abzuwägen und andere Modelle zu berücksichtigen, wenn sie nicht die beste Lösung für Dein spezifisches Datenproblem ist.
Insgesamt ist logistische Regression jedoch eine leistungsstarke Methode in der Datenwissenschaft, die Dir dabei helfen kann, Vorhersagen für binäre Klassifikationsprobleme zu treffen und Einblicke in die Beziehung zwischen Variablen zu gewinnen. Es lohnt sich also definitiv, sich mit dieser Methode vertraut zu machen und sie in Deinem Datenanalyse-Toolkit zu haben!