Von Statistiken über die Untersuchung von Körperbewegungen bis hin zu Börsenkursen für Finanzaktien werden Funktionen in allen Bereichen verwendet. Jedes Mal, wenn du eine Taste auf einer Computertastatur drückst oder ein Mobiltelefon bedienst, kannst du dir vorstellen, dass im Hintergrund mehrere Funktionen abwechselnd Transformationen anwenden und ein Ergebnis liefern.
In diesem Artikel geht es darum, einige wichtige Punkte zu erläutern, um zu verstehen, was eine Funktion ist.
1. Definition einer Funktion und einige Beispiele
Eine Funktion ist in der Mathematik die Definition eines Ergebnisses, das mit einem Wert aus einem Eingabebereich verknüpft ist. Das Ergebnis kann durch verschiedene arithmetische Operationen oder Verfahren (wie z. B. das Lösen von Gleichungen oder Grenzwertüberschreitungen) erzielt werden.
Als Beispiel für eine formale Definition kann die folgende mathematische Definition dienen:
Eine Funktion f ist eine Möglichkeit, jeder reellen Zahl x eine einzige reelle Zahl y zuzuordnen.
In der obigen Beispieldefinition:
x ist die Variable der Funktion (bei Funktionen mit nur einer Variablen).
y ist das Bild der Variablen x durch f (das Bild einer Funktion f(x) oder y = f(x)).
Die Zuordnung einer Zahl zu einer anderen kann auf verschiedene Weise erfolgen:
Durch eine mathematische Formel (Beispiel: f(x) = 4x + 10).
Durch eine Kurve (z. B. eine Kurve, die die Temperatur in Abhängigkeit von der Zeit zeigt).
Mithilfe eines Messinstruments (z. B. eines Stromzählers).
Mithilfe einer Wertetabelle, die die Übereinstimmung zwischen zwei Wertelinien angibt.
Die tatsächliche Berechnung des Ergebnisses kann mithilfe von Computerfunktionen erfolgen, die Operationen mit den Eingabedaten durchführen. Die Computerfunktion besteht dann aus der Beschreibung der Methode, mit der ein Ergebnis aus den Eingabeparametern erzielt werden kann (Algorithmus).
In der Mengenlehre kann eine Funktion als die Beziehung zwischen zwei Mengen definiert werden, die jedem Element der Ausgangsmenge ein oder mehrere Elemente der Zielmenge zuordnet.
2. Allgemeines Prinzip und Beispiele für Funktionen
Wenn wir 2 Gruppen von Zahlen betrachten (eine Start- und eine Zielgruppe unten) :
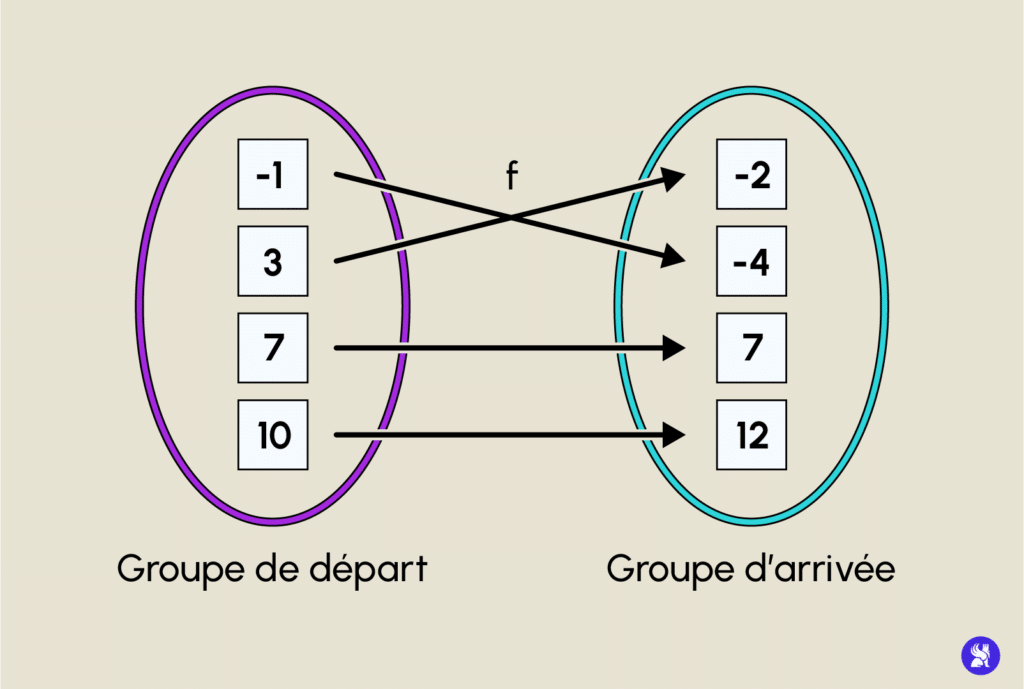
Die Zuordnung der beiden Gruppen erfolgt durch die Funktion f (die übrigens auch einen anderen Namen als f haben könnte). Auf der Grundlage dieser Darstellung kann man leicht erkennen, dass man f durch die folgende tabellarische Schreibweise ersetzen könnte:
Als Interpretation werden alle Zahlen in der Ankunftsmenge als Bilder der Zahlen in der Ausgangsmenge bezeichnet. Alle Zahlen in der Startmenge sind die Vorgänger der Zahlen in der Zielmenge.
Um eine Funktion in der Mathematik genau zu definieren, ist es in der Praxis notwendig, die verschiedenen Eigenschaften der Funktion wie Regelmäßigkeit, Variation, Integrierbarkeit usw. zu definieren.
Zu diesem Zweck gibt es verschiedene Arten von Funktionen, wie z. B. :
Konstante Funktionen, die immer das gleiche Ergebnis mit einer Reihe von Werten verknüpfen (z. B. f(x) = 5).
Lineare Funktionen, die immer die Form f(x) = ax haben (a ist eine Zahl).
Affine Funktionen (die in mehreren Machine-Learning-Algorithmen verwendet werden) in der Form f(x) = ax + b (a und b sind Zahlen).
3. Definitionsmenge einer Funktion
Der Definitionsbereich einer Funktion f ist die Menge aller Zahlen in der Ausgangsmenge, die ein Bild durch die Anwendung von f besitzen.
Zum Beispiel ist der Definitionsbereich der Funktion mit einer Variablen f(x) = 1/x D = (-, 0)U(0, +), wobei 0 ausgeschlossen ist, da eine Division durch 0 nicht möglich ist.
Die Definition einer Funktion kann dann in der folgenden Form erfolgen:
f: D→R
X→f(x)
Die Definition zeigt deutlich die Übereinstimmung zwischen den Elementen von D, die ein Bild f(x) in R (hier die Menge der reellen Zahlen) haben.
4. Grafische Darstellung einer Funktion
Die grafische Darstellung einer Funktion entspricht der visuellen Darstellung der Funktion in einem Raum, den man als Koordinatensystem festlegt. In zwei Dimensionen wird meist ein orthonormaler Raum (O, I, J) verwendet, der einem Raum entspricht, in dem die Punkte O, I und J ein rechtwinkliges Dreieck bilden, das in O gleichschenklig ist (O ist der Ursprung des Koordinatensystems).
Die Geraden OI und OJ stellen die Abszissen- bzw. Ordinatenachse dar.
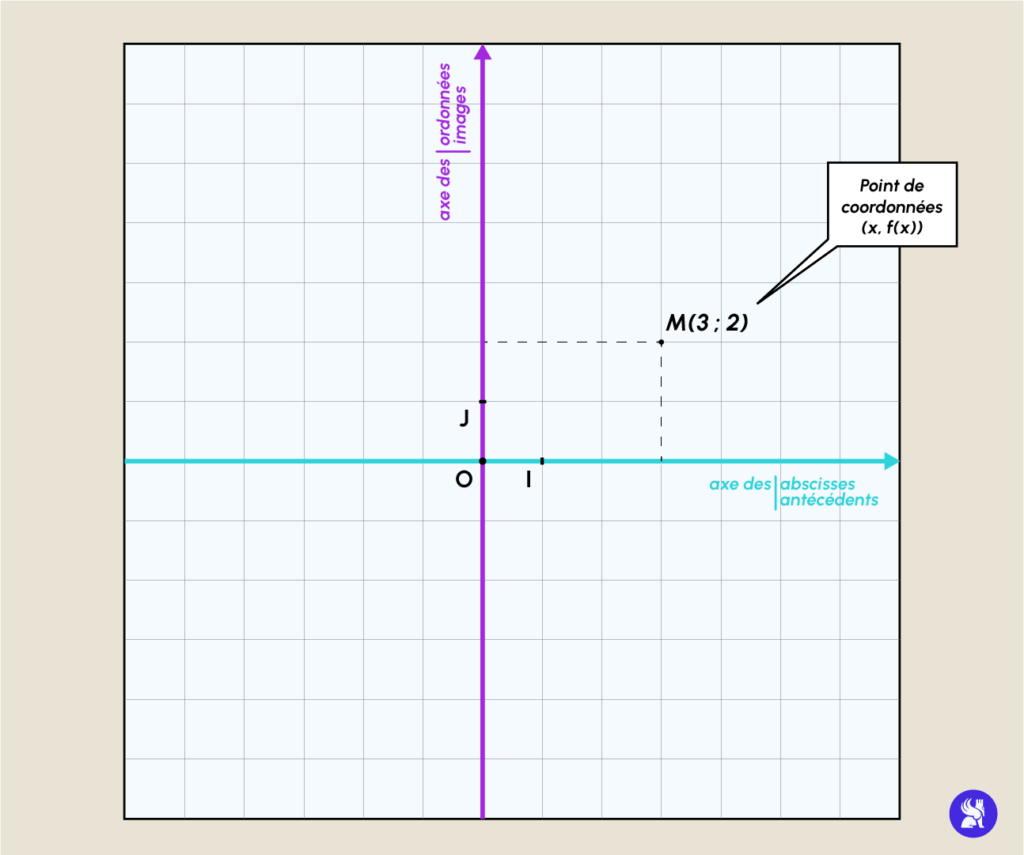
Gegeben sei f eine Funktion und D die zugehörige Definitionsmenge. In einem orthonormalen (oder orthogonalen) Koordinatensystem (O, I, J) wird die Menge der Punkte M mit den Koordinaten (x, f(x)), wobei x einen Bereich D beschreibt (man spricht auch oft von einem Intervall I), als Repräsentationskurve oder grafische Darstellung (mit Cf bezeichnet) der Funktion f bezeichnet. Man sagt dann, dass Cf (die repräsentative Kurve der Funktion f) die Gleichung y = f(x) hat.
Außerdem stellt die Abszissenachse (horizontal) die Vorgänger (also die x) und die vertikale Achse die Bilder (die f(x)) dar.
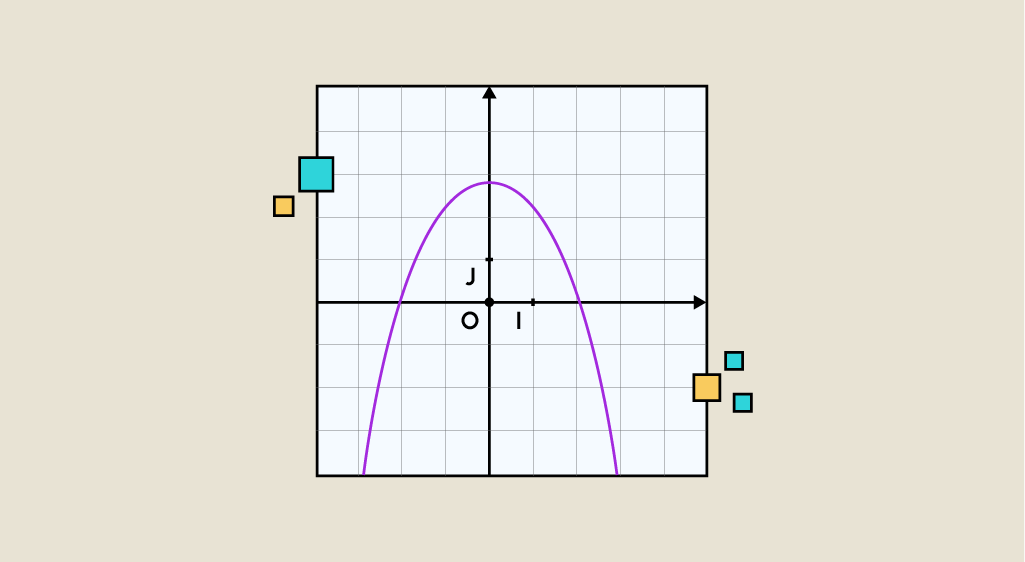
Im obigen Beispiel bedeutet f(-1) = -4, dass Cf durch den Punkt mit den Koordinaten (-1, -4) geht. Auf diese Weise beschreibt Cf die Menge aller Punkte, die die Gleichung y = f(x) erfüllen.
5. Variationsrichtung und Extrema einer Funktion
Die Variabilität einer Funktion ist eine Eigenschaft, die systematisch untersucht wird.
Sei eine Funktion f, die auf einem Intervall I definiert ist. Es gibt mehrere Möglichkeiten, wie die Funktion f auf I variabel sein kann:
- f kann steigend sein: Man sagt, dass f auf I steigend ist, wenn für jedes x und x‘ in I gilt: Wenn x < x‘, dann f(x) f(x‘).
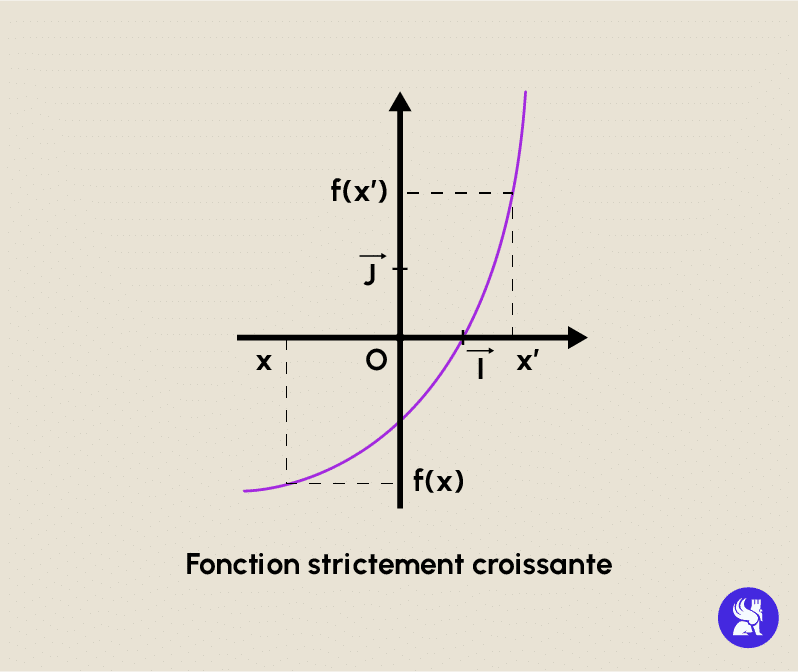
- f kann streng steigend sein: f ist in I streng steigend, wenn für alle x und x‘ in I gilt: Wenn x < x‘, dann gilt f(x) f(x‘).
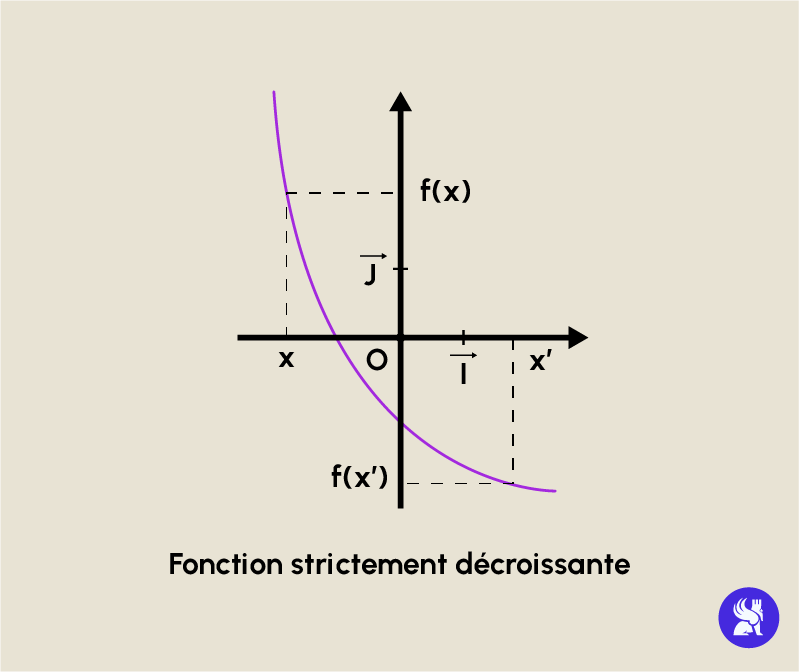
- f peut être décroissante : on dit que f est décroissante sur I si pour tout x et x’ dans I on vérifie: si x < x’ alors f(x) f(x‘).
- f peut être strictement décroissante : on dit que f est strictement décroissante sur I si pour tout x et x’ dans I on vérifie: si x < x’ alors f(x) f(x‘).
- f kann konstant sein: Wir sagen, dass f konstant ist, wenn es eine Konstante d gibt, so dass für jedes x in I f(x) = d gilt.
- f kann monoton sein: Man sagt, dass f monoton ist, wenn f in I zunimmt oder (oder ausschließlich) in I abnimmt.
- f kann strikt monoton sein: Man sagt, dass f strikt monoton ist, wenn f auf I strikt ansteigend oder strikt fallend ist.
Wenn eine Funktion steigend oder streng steigend ist, werden die Bilder f(x) in der gleichen Reihenfolge wie die Vorgänger angeordnet. Man sagt dann, dass f die Reihenfolge beibehält.
In der Praxis wird die Variabilität einer Funktion f mithilfe der Variationstabelle (in zwei Zeilen) untersucht, die dabei hilft, die Variationen der Funktion zusammenzufassen:
Die erste Zeile der Variationstabelle enthält die Intervalle der Definitionsmenge der Funktion. Hier werden die Werte der Ausgangsmenge (die Abszisse) angegeben, bei denen sich die Richtung der Variation der Funktion ändert.
In der zweiten Zeile der Tabelle werden Pfeile eingezeichnet, die die Änderungsrichtung der Funktion darstellen.
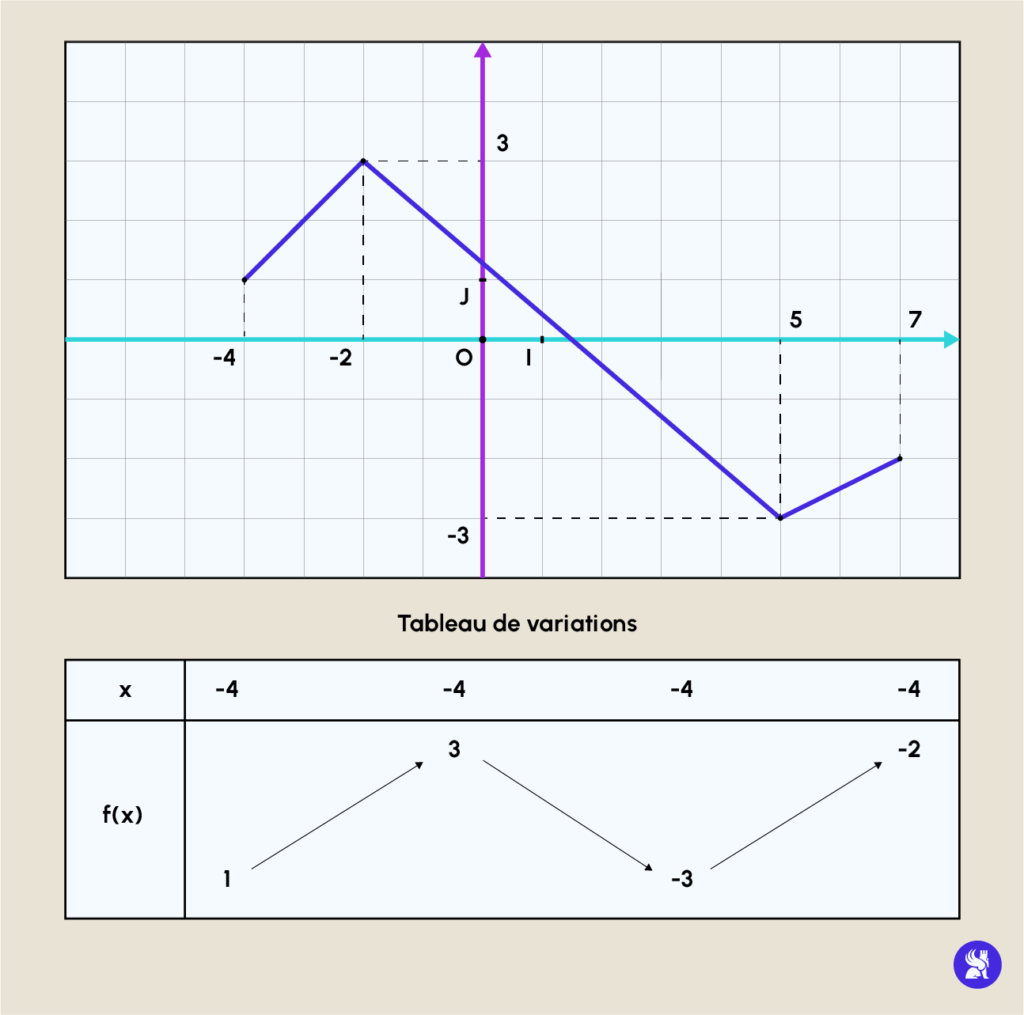
Der Maximalwert M und der Minimalwert m einer Funktion f auf dem Intervall I entsprechen dem größten bzw. dem kleinsten Wert von f(x), wobei x in I variiert. Im obigen Beispiel erreicht f seinen Maximalwert an dem Koordinatenpunkt (-2, 3) (3 ist das Maximum der Funktion) und seinen Minimalwert an dem Punkt (5, -3). Die Maximal- und Minimalwerte werden als Extremwerte der Funktion bezeichnet.
6. Funktionen in der Datenwissenschaft
In der Datenanalyse werden Funktionen auf allen Ebenen verwendet. In Python zum Beispiel sind die Bibliotheken, die verwendet werden, um Transformationen auf Daten anzuwenden, Funktionspakete. Je nachdem, was du tun möchtest (z. B. Text oder Bilder manipulieren), wirst du ein Funktionspaket verwenden, das auf die Manipulation eines bestimmten Datentyps ausgerichtet ist.
In Python gibt es Funktionen für so ziemlich alles (vom Lesen über das Speichern bis hin zur Umwandlung von Daten oder Dateien).
Auch interessant: