"Wenn Du die blaue Pille nimmst, ist die Geschichte zu Ende, Du wachst in Deinem Bett auf und glaubst, was Du willst. Nimmst du die rote Pille, bleibst du im Wunderland und ich zeige dir, wie weit der Kaninchenbau geht." Die Wahrheit kennen oder in seiner Bequemlichkeit bleiben, die Matrix entdecken oder nur ein Objekt in ihr bleiben.
Diese Entscheidung aus dem Film Matrix hat ganze Generationen zum Träumen gebracht und die Matrix ist zu einer legendären Ikone der Popkultur geworden, die in den allgemeinen Wortschatz eingegangen ist.
Bevor sie jedoch ein von Maschinen entwickeltes System war, das Menschen wie Wegwerfbatterien ausnutzt, waren Matrizen mächtige mathematische Werkzeuge, die in vielen Bereichen von der linearen Algebra über Markov-Modelle und das Lösen von Gleichungssystemen bis hin zur Wahrscheinlichkeitsrechnung von großer Bedeutung waren.
In diesem Artikel werden wir dieses Werkzeug vorstellen und seine ersten Eigenschaften betrachten, sowie Wege aufzeigen, wie sie in Python implementiert werden können.
Was ist eine Matrix ?
In der Mathematik entspricht eine Matrix einer Tabelle von Elementen. Sie wird durch ihre Dimension (die Anzahl der Zeilen und Spalten) und durch die verschiedenen Elemente, die darin vorkommen, definiert.
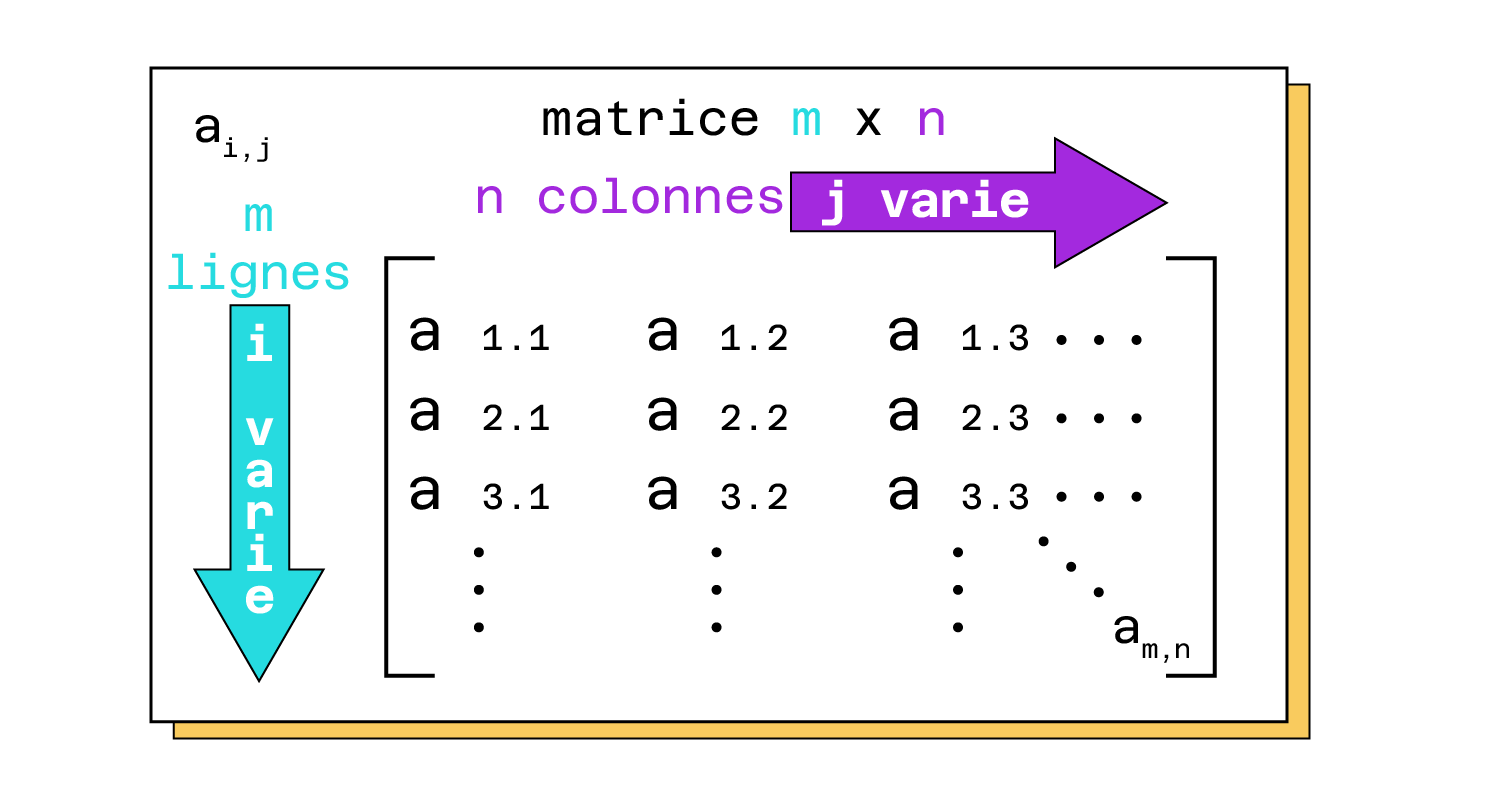
In dieser Matrix steht n für die Anzahl der Spalten, m für die Anzahl der Zeilen, i und j sind die Indizes, mit denen man ein Element finden kann (ähnlich wie bei Koordinaten).
Die verschiedenen üblichen Matrizen
- Eine Matrix, die nur aus leeren Elementen besteht, wird als Nullmatrix bezeichnet.
- Wenn es die gleiche Anzahl an Zeilen wie Spalten gibt, spricht man von einer quadratischen Matrix.
- Eine quadratische Matrix, die außer auf der Diagonalen nur Null-Elemente hat, wird Diagonalmatrix genannt.
- Eine diagonale Matrix, die nur auf der Diagonalen Einsen hat, wird Identitätsmatrix genannt.
- Eine quadratische Matrix, die nur Elemente unterhalb der Diagonalen hat, heißt untere Dreiecksmatrix
- Eine quadratische Matrix, die nur Elemente oberhalb der Diagonale enthält, wird als obere Dreiecksmatrix bezeichnet.
Operationen mit Matrizen
Es gibt viele Operationen, die wir auf Matrizen oder zwischen ihnen durchführen können, wodurch wir neue Matrizen erhalten. Die häufigsten sind die folgenden
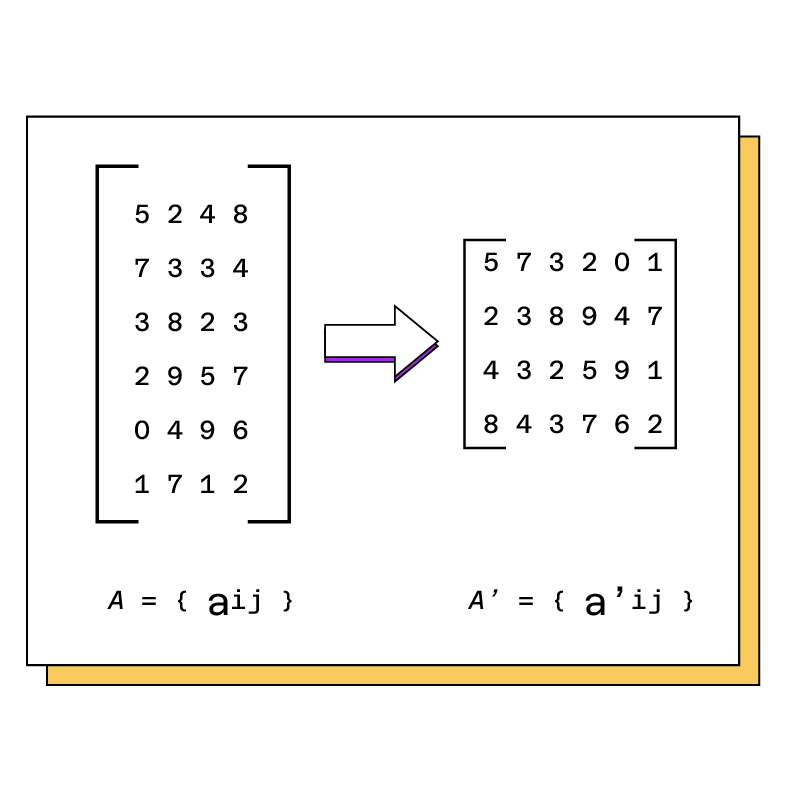
- Transponieren: Transponieren ist die Transformation, die Zeilen in Spalten und umgekehrt verwandelt, ähnlich wie bei einem Spiegel.
- Addition: Die Addition zwischen gleichdimensionalen Matrizen ist gleichbedeutend mit der Addition jedes einzelnen Elements der Matrizen.
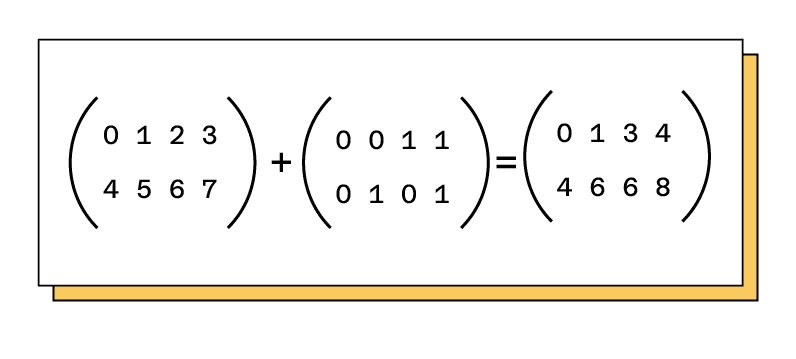
- Multiplikation mit einem Skalar: Die Multiplikation einer Matrix mit einem Skalar entspricht der Multiplikation jedes Elements mit diesem Skalar (Multiplikation mit k entspricht der k-fachen Addition der Elemente zueinander).
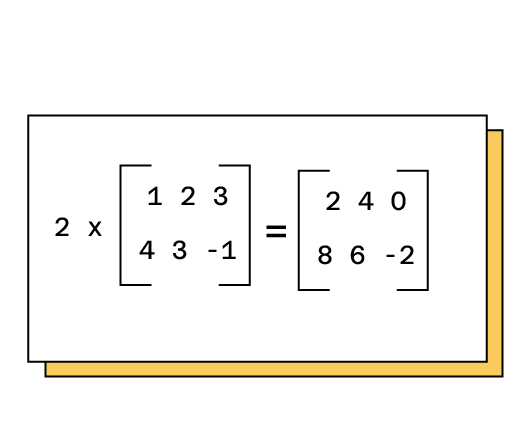
- Das Matrixprodukt: Das Produkt einer Zeilenmatrix mit einer Spaltenmatrix ist wie folgt definiert:
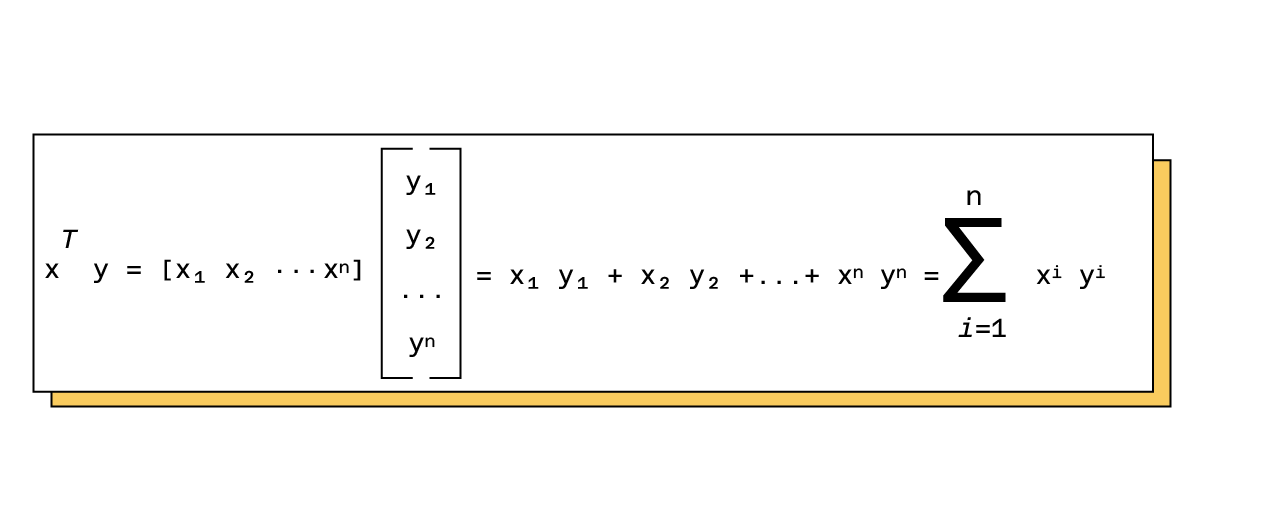
Ausgehend von dieser Definition können wir das Matrixprodukt zwischen zwei Matrizen definieren. Jedes Element mit dem Index i,j in der Produktmatrix entspricht dem Produkt der i-ten Zeile und der j-ten Spalte. Beispiel:
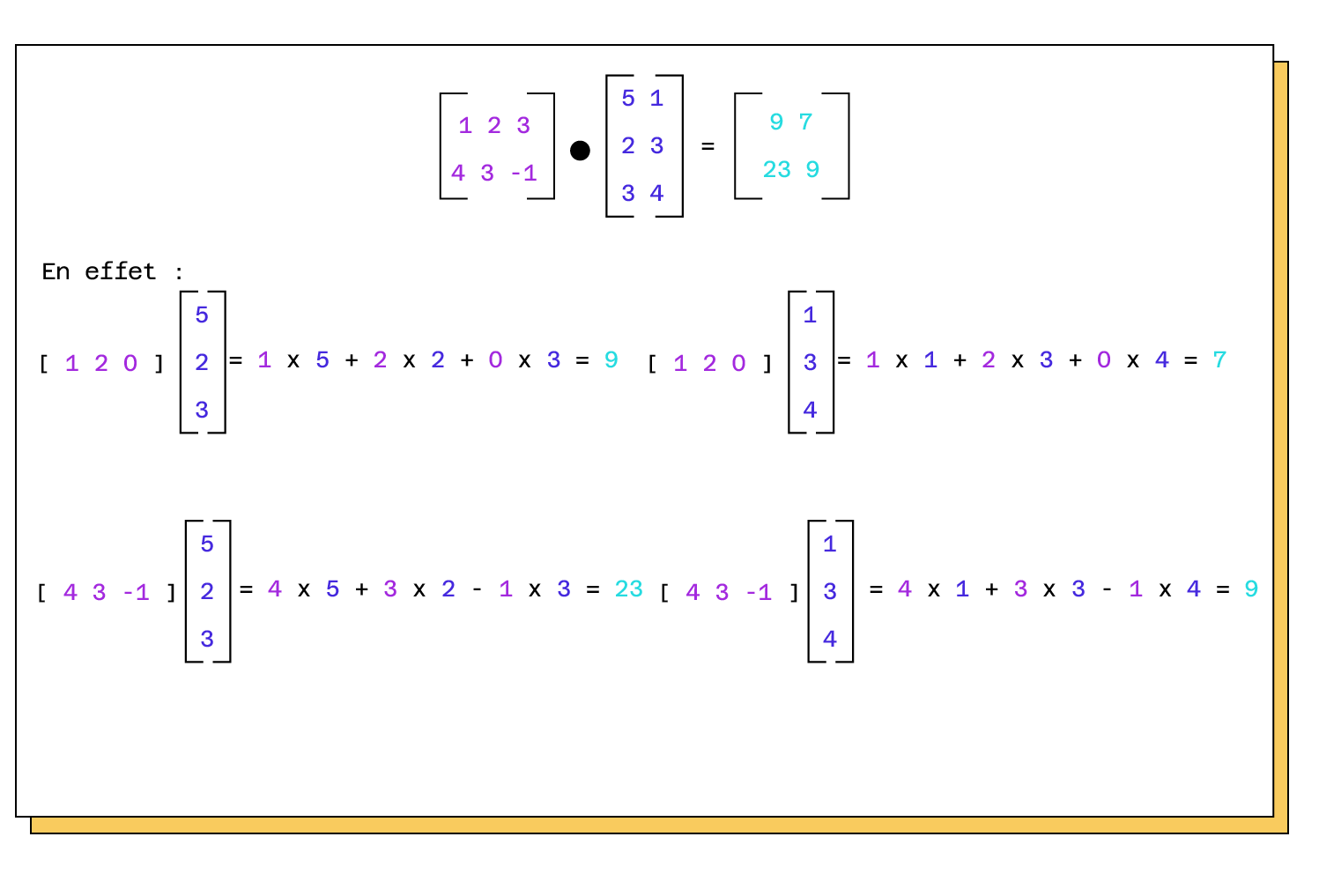
Achtung: Die erste Matrix muss die gleiche Anzahl an Zeilen haben wie die zweite Matrix an Spalten und umgekehrt, damit das Produkt richtig funktioniert.
Eigenschaften des Matrixprodukts
- assoziativ : ABC = (AB)C = A(BC)Das Matrixprodukt ist:.
- Die Einheitsmatrix I ist neutrales Element für die Multiplikation: AIm = InA = A, wenn die Matrix A die Abmessungen n × m hat. </li
- Transponiert von einem Produkt: (AB) T = BTAT (Achte auf die Änderung der Reihenfolge! ).</li
- Inverse einer Matrix:Wenn es für eine quadratische Matrix A eine Matrix B gibt, die so beschaffen ist, dass AB den Wert der Identität hat, dann hat BA ebenfalls den Wert der Identität, B ist eindeutig und wird die Inverse von A genannt. Allgemeiner ausgedrückt: Die Inverse einer Matrix A ist A-1 .
Implementation in Python
Um Matrizen in Python zu implementieren, kann man auf zweidimensionale Listen oder Numpy-Arrays zurückgreifen. Hier ist ein Skript mit Anwendungsbeispielen:









