Die Huffman Kodierung ist ein Algorithmus zur Datenkomprimierung. Die Idee dahinter ist, den Eingabezeichen Codes mit variabler Länge zuzuweisen. Die Länge der zugewiesenen Codes basiert auf der Häufigkeit, mit der die Zeichen in der ursprünglichen Sequenz vorkommen.
Die Huffman Codierung ist ein Algorithmus zur verlustfreien Datenkomprimierung. Dieser Algorithmus wurde 1952 von David Albert Huffman erfunden.
Die Huffman-Kodierung ist im Allgemeinen wichtig, um Daten zu komprimieren, in denen es Zeichen gibt, die häufig vorkommen. Der Faktor Häufigkeit wird hierbei aufgrund des Konzepts der Informationsentropie berücksichtigt, denn je häufiger ein Zeichen auftritt, desto höher ist die Entropie dieses Zeichens.
Wie funktioniert die Huffman-Codierung?
Das Prinzip der Huffman Codierung beruht auf dem Aufbau einer Baumstruktur mit Knoten.
Dieser Algorithmus basiert auf der Idee, dass die beste Art und Weise, eine Information zu kodieren, darin besteht, die optimale Länge zu finden, um jedes Zeichen in der ursprünglichen Sequenz darzustellen.
Die optimale Länge des Codes für ein Zeichen wird durch die Anzahl der Zweige bestimmt, die man von der Spitze des Huffman Baums aus durchlaufen muss, um zu diesem Zeichen zu gelangen, das immer ein Blatt des Huffman-Baums ist.
Die Idee hinter dem Huffman-Baum ist es, die Länge der Symbole, die man zur Verschlüsselung einer Nachricht verwendet, zu minimieren, und das bedeutet, die Größe des Huffman-Baums zu minimieren. Man könnte sich jedoch fragen, wie der Huffman-Baum aufgebaut ist.
Was ist das Prinzip der Huffman Codierung?
Was die Konstruktion des Baumes betrifft, so werden jedes Mal die beiden Knoten mit dem geringsten Gewicht miteinander verbunden, um einen neuen „Vater“-Knoten zu erhalten, dessen Gewicht der Summe der Gewichte seiner Söhne entspricht.
Dieser Vorgang wird so lange wiederholt, bis nur noch ein einziger Knoten übrig bleibt: die Wurzel des Huffman-Baums, deren Gewicht der Summe der Gewichte aller ursprünglichen Blattknoten entspricht.
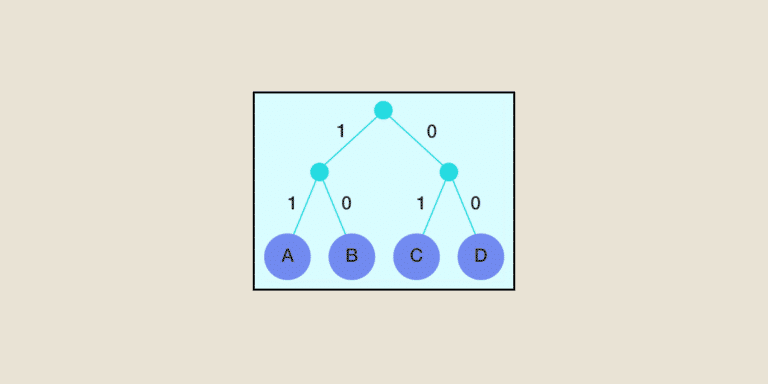
Dann wird z. B. jeder Abzweigung, die nach links führt, der Code 0 und jeder Abzweigung, die nach rechts führt, der Code 1 zugeordnet.
Um den binären Code jedes Zeichens zu erhalten, durchläuft man den Baum von der Spitze bis zu den Blättern und nimmt jedes Mal das Zeichen 0 oder 1 von den Zweigen, die man durchläuft, je nachdem, ob man von rechts oder von links kommt.
Die einzelnen Schritte beim Bau des Huffman Tree
- Erstelle Blattknoten aus jedem Zeichen der zu verschlüsselnden Nachricht, wobei jedes Zeichen nur einmal mit den verschiedenen Häufigkeiten des Auftretens der Zeichen berücksichtigt wird, die nach Priorität geordnet werden sollen, wobei die Zeichen mit den niedrigsten Häufigkeiten Vorrang haben.
- Extrahiere die beiden Knoten mit der niedrigsten Gewichtung in aufsteigender Reihenfolge der Häufigkeit, d. h. der Knoten mit der niedrigsten Häufigkeit muss zuerst extrahiert werden.
- Erstelle einen neuen internen Knoten mit einer Häufigkeit, die der Summe der Häufigkeiten dieser beiden Knoten entspricht. Definiere den ersten extrahierten Knoten als den linken Sohn dieses Knotens und den zweiten Knoten als den rechten Sohn. Füge den neu erstellten Knoten zur Liste der verbleibenden Knoten hinzu.
- Wiederhole die Schritte 2 und 3, bis du durch alle Knoten gegangen bist, die du in Schritt 1 erhalten hast. Der verbleibende Knoten ist die Wurzel des Baumes und die Konstruktion ist abgeschlossen.
Ein Beispiel zur Veranschaulichung der Verschlüsselung
Um die Idee der Huffman Codierung zu veranschaulichen, betrachten wir die unten stehende Nachricht, die wir optimal in binärer Form darstellen werden:
aabbccddbbeaebdddfffdbffddabbbbbcdefaabbcccccaabbddfffdcecc
Bei einer zu kodierenden Nachricht wie dieser beginnen wir zunächst damit, die Häufigkeit der verschiedenen Zeichen in der Nachricht zu zählen. Nach der Zählung erhalten wir das folgende Ergebnis:
a:8, b:15, c:11, d:12, e:4, f:9
Wir werden den Algorithmus der Huffman Codierung an diesem Beispiel implementieren.
Der erste Schritt besteht darin, die am wenigsten häufigen Zeichen in der zu kodierenden Nachricht zu verwenden. Wir müssen also mit den Buchstaben ‚e‘ und ‚a‘ beginnen, die die geringsten Häufigkeiten haben, und dann ihre Gewichte summieren, d. h. die Häufigkeiten ihres Auftretens summieren, um die beiden Zeichen durch ein neues, einzigartiges Zeichen zu ersetzen, dessen Häufigkeit der Summe der Häufigkeiten dieser beiden Zeichen in der Liste entspricht. Nach diesem ersten Schritt sieht die Liste wie folgt aus
new node:12, b:15, c:11, d:12, f:9
wobei der Knoten new node die Knoten a und e mit einem Gewicht ersetzt, das der Summe ihrer jeweiligen Gewichte entspricht. [ new node : 12 = (a:8, e:4)]]
Dann wählst du aus der neuen Liste die beiden Elemente mit dem geringsten Gewicht aus und iterierst den Prozess, bis du den Knoten mit dem höchsten Gewicht erhältst, d.h. mit dem Gewicht der Summe der Häufigkeiten aller Zeichen. Am Ende des Aufbaus des Huffman-Baums sind alle verschiedenen Zeichen der ursprünglichen Nachricht, die codiert werden soll, Blätter des Huffman-Baums, die auch als Leaf Nodes bezeichnet werden. Am Ende der Ausführung erhält man die folgenden Ergebnisse:
d -> 00
e -> 010
a -> 011
b -> 10
f -> 110
c -> 111
Wir erinnern uns, dass die Etiketten des Huffman-Baums markiert werden, indem wir die Konvention anwenden, eine 0 auf das linke Etikett und eine 1 auf das rechte Etikett in absteigender Reihenfolge zu setzen, d.h. von der Wurzel des Baums bis zu den Blättern.
Die zeitliche Komplexität dieses Algorithmus ist quasi-linear, d.h. in O(nlogn), wobei n die Anzahl der eindeutigen Zeichen in der zu komprimierenden Liste ist, und die räumliche Komplexität ist linear, d.h. in O(n).
Wozu dient die Huffman codierung im Berufsleben?
Zu den verschiedenen Anwendungen des Huffman-Codieralgorithmus für die Datenkomprimierung gehören die Übertragung von Faxen und Texten, konventionelle Komprimierungsformate wie GZIP, Multimedia-Software wie JPEG, PNG und MP3.
Im Allgemeinen ist die Datenkomprimierung nützlich, um die Speicherkapazität des Arbeitsspeichers oder die Geschwindigkeit der Datenübertragung zu erhöhen.
Bei der Erstellung des Baums gibt es Varianten der Huffman Codierung.
Entweder ist das Wörterbuch statisch: Jedes Zeichen hat einen vordefinierten Code, der bekannt ist oder im Voraus veröffentlicht wird (und daher nicht übertragen werden muss) ;
- Das Wörterbuch ist semi-adaptiv: Der Inhalt wird analysiert, um die Häufigkeiten der einzelnen Zeichen zu berechnen, und ein optimierter Baum wird zur Kodierung verwendet (er muss dann zur Dekodierung übertragen werden);
- Oder das Wörterbuch ist adaptiv: Ausgehend von einem bekannten Baum (der vorher veröffentlicht und daher nicht übertragen wurde) wird dieser während der Komprimierung verändert und nach und nach optimiert. Die Berechnungszeit ist viel länger, bietet aber oft eine bessere Kompressionsrate.
Letztendlich ist die Huffman Codierung ein sehr nützlicher Algorithmus zur Datenkomprimierung, der heutzutage mehrere Anwendungen hat, von der Erhöhung der Speicherkapazität bis hin zur Erhöhung der Datenübertragungsgeschwindigkeit. Die dynamische Variante ist eine Verbesserung der statischen Variante, deren Prinzip in diesem Artikel vorgestellt wurde.