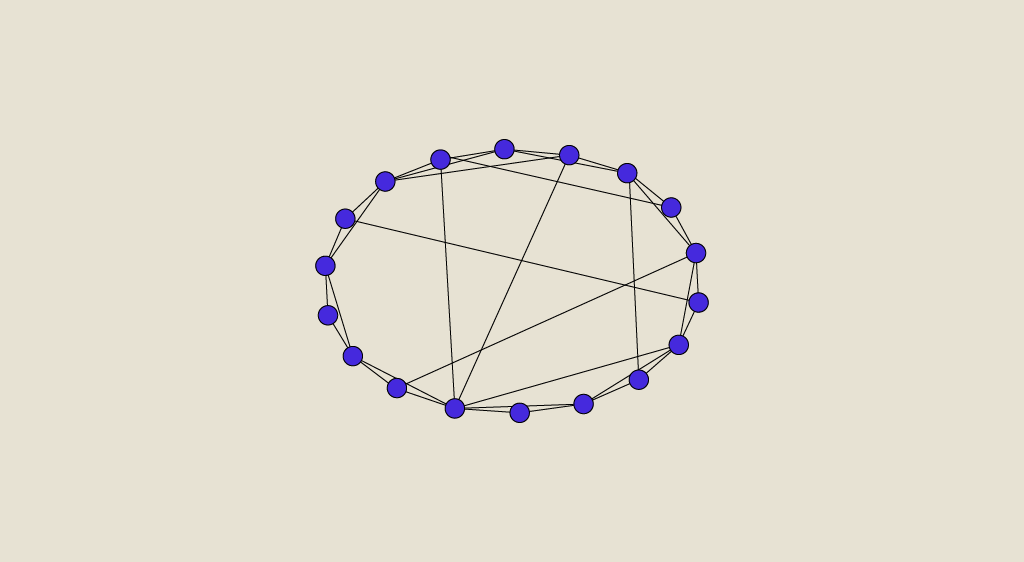
NetworkX ist eine sehr nützliche Python-Bibliothek, mit der du deine Daten in Form von Graphen modellieren kannst. Sie enthält auch einige klassische graphentheoretische Algorithmen (Dijkstra, PageRank, SImRank...), die wir in diesem Artikel vorstellen werden.
NetworkX : Was ist ein Graph? Einführung in die Graphentheorie
Ein Graph ist eine Menge von Knoten (die für Personen, Städte, Produkte, Text, Bilder usw. stehen) und Kanten, die eine Teilmenge dieser Knoten verbinden. Der Grad eines Knotens in einem Graphen ist die Anzahl seiner Nachbarn (Gipfel, die durch Kanten mit ihm verbunden sind).
Die Kanten können einseitig oder symmetrisch sein, ein Graph kann also gerichtet oder ungerichtet sein.
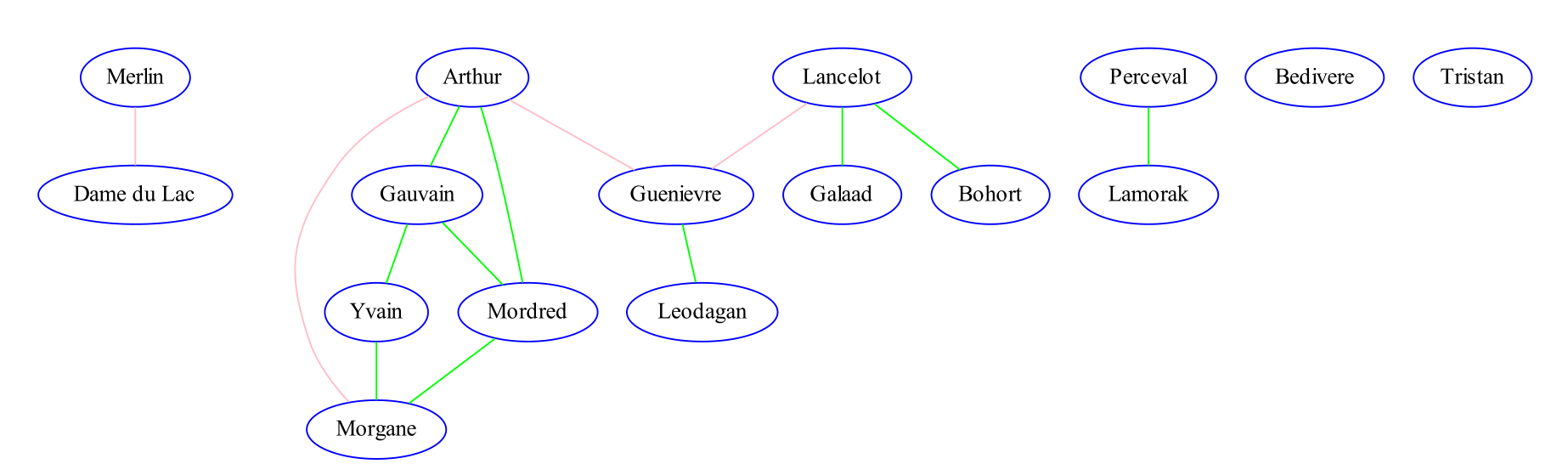
Der ungerichtete Graph stellt die Verwandtschafts- (grün) und Liebesbeziehungen (rosa) der Hauptfiguren der Tafelrunde dar:
Der folgende gerichtete Graph stellt eine Liste von Aufgaben dar, die beim Bau eines Hauses erledigt werden müssen:
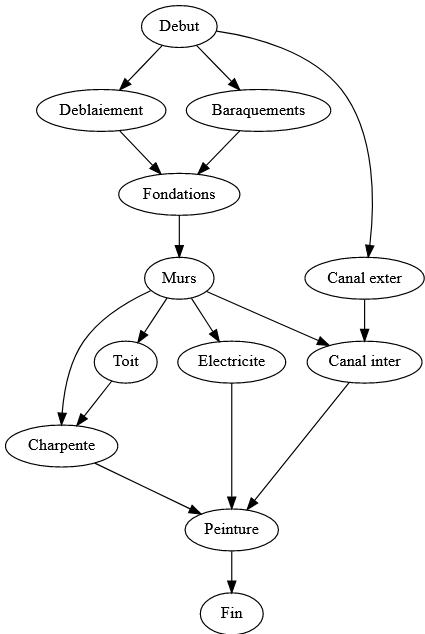
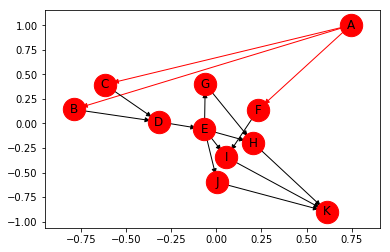
Man kann sich dafür entscheiden, die Kanten eines Graphen mit Gewichten zu gewichten, die die Kosten oder den Anteil der Nutzung dieses Pfades modellieren. Im obigen Graphen wären die Kosten der Kanten z. B. die Anzahl der Tage, die benötigt werden, um die Aufgabe zu erledigen.
Anwendung mit NetworkX:
Die Graphentheorie deckt ein breites Spektrum an Anwendungen ab: Modellierung von Netzwerken (Infrastruktur, soziale Netzwerke usw.), Lagerverwaltung, Zeitplanung und die damit verbundenen Probleme:
- Wie kann die kürzeste/optimale Route festgelegt werden?
- Wie platziert man Infrastruktur (Strom, Glasfaser…) optimal? Problem der minimalen Abdeckung.
- Wie kann man Mieten an Kunden oder Kurse an Lernende zuweisen, ohne dass es zu Überschneidungen kommt?
- Problem der Einfärbung.
Auch interessant: Scatter-Plot
Grundlegende Funktionen und Hauptverwendungszwecke von NetworkX
Erstellen unseres ersten Graphen:
Der folgende Code erstellt einen Graphen.
Du fügst zunächst seine Kanten (g.addnode) und Knoten (g.add edge) hinzu (du kannst mehrere Knoten auf einmal mit den Funktionen g.add nodes from und g.add edges from hinzufügen), dann zeigst du den Graphen an:
Mit den Methoden von NetworkX kann man auch schnell Eigenschaften des Graphen synthetisieren:
- Anzahl der Knoten mit number_of_nodes, Anzahl der Kanten mit number_of_edges.
- Durchmesser = maximale Entfernung zwischen zwei Knoten: diameter
Die sieben Brücken von Königsberg, was ist dies für ein historisches Ereignis?
Eines der ersten Probleme der Graphentheorie ist das Problem der Brücken von Königsberg. Es wurde 1736 dem Mathematiker Euler in folgender Form vorgelegt:
„Kann man die sieben Brücken der Stadt durchlaufen, indem man jede Brücke nur einmal benutzt?“: Euler stellte fest, dass die Reihenfolge des Weges keinen Einfluss hat und modellierte das Problem als Graph: Die verschiedenen Stadtteile sind seine Knoten, die durch die Brücken miteinander verbunden sind, die wiederum die Kanten des Graphen sind.
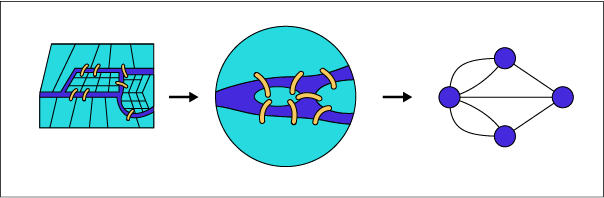
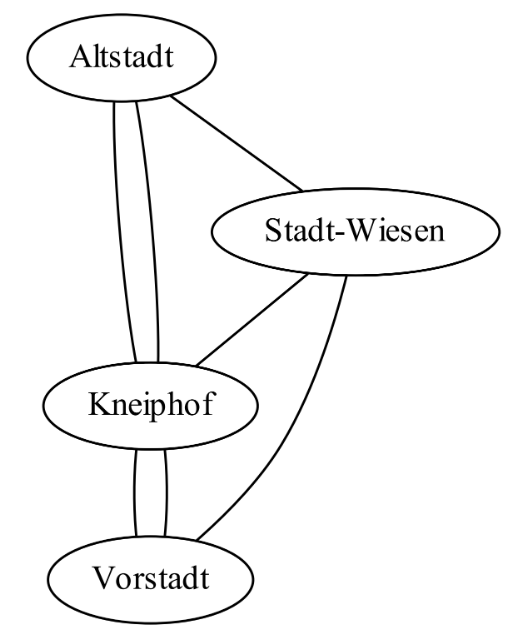
Was ist deiner Meinung nach also die Lösung?
Wenn man über eine Brücke in einen Stadtteil kommt, muss man ihn auch über eine (andere) Brücke wieder verlassen. Die Anzahl der Ankünfte in einem Stadtteil ist also gleich der Anzahl der Abfahrten aus diesem Stadtteil. Daraus folgt, dass jeder Stadtteil über eine gerade Anzahl von Brücken mit den anderen verbunden sein muss.
Die Lösung des Problems hängt also vom Grad (Anzahl der angrenzenden Nachbarn/Brücken) der Knoten ab: Wenn alle Knoten gerade sind, dann gibt es einen Weg, der alle Brücken nur einmal überquert, den sogenannten Eulerschen Weg.
Wie findet man den kürzesten Weg mit dem Problem des Handelsreisenden?
Ein weiteres klassisches Problem der Graphentheorie ist das Problem des Handelsreisenden: Die Knoten des Graphen sind eine Reihe von Städten oder Kunden, die beliefert werden müssen, während die Kanten die Straßeninfrastruktur sind, die mit einem Gewicht versehen sind, das die damit verbundene Entfernung modelliert. Es wird versucht, alle Städte auf dem kürzesten Weg zu beliefern.
Für den Fall, dass die Gewichte des Graphen positiv sind (oder es zumindest keine Zyklen mit negativem Gewicht gibt), wird eine Lösung für dieses Problem durch den Dijkstra-Algorithmus gegeben, der über die Funktion nx.shortest_path() verfügbar ist.
Ein schlauer Trainer versucht, das Abenteuer mit möglichst wenigen Pfaden zu beenden:
Minimale Abdeckung eines Netzwerks
Das Problem des Minimal Covering Tree tritt auf, wenn ein Unternehmen versucht, ein Netzwerk (Öl, Glasfaser) zu bauen, das eine Reihe von Haushalten optimal verbindet.
In dem mit diesem Problem verbundenen Graphen sind die Knoten die zu verbindenden Kunden, die Kanten die Menge der möglichen Infrastrukturstandorte und die Gewichte die Kosten für den Bau.
Es wird versucht, die Teilmenge der Kanten zu bestimmen, die alle Knoten verbindet und die Gesamtkosten minimiert, was als minimaler Deckungsbaum bezeichnet wird.
NetworkX verfügt über eine Funktion, die dieses Problem löst: der Kruskal-Algorithmus, der in der Methode nx.tree.minimum_spanning_tree implementiert ist.
Ein Industrieller will ein Eisenbahnnetz in der fiktiven Provinz Costaguana bauen. Er will alle Städte miteinander verbinden, hat aber nur ein begrenztes Budget:
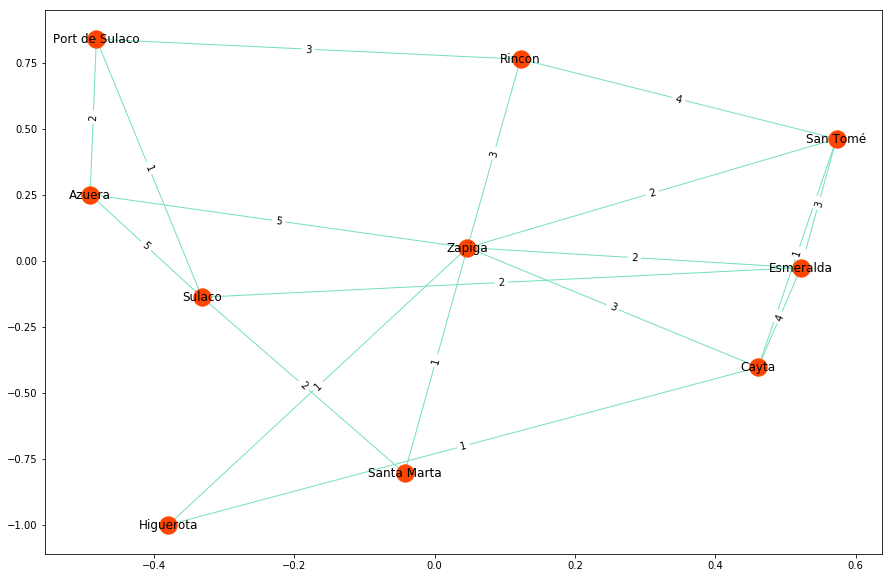
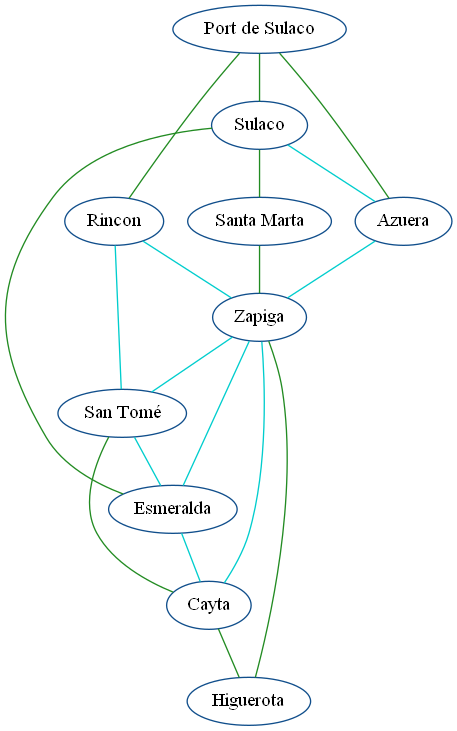
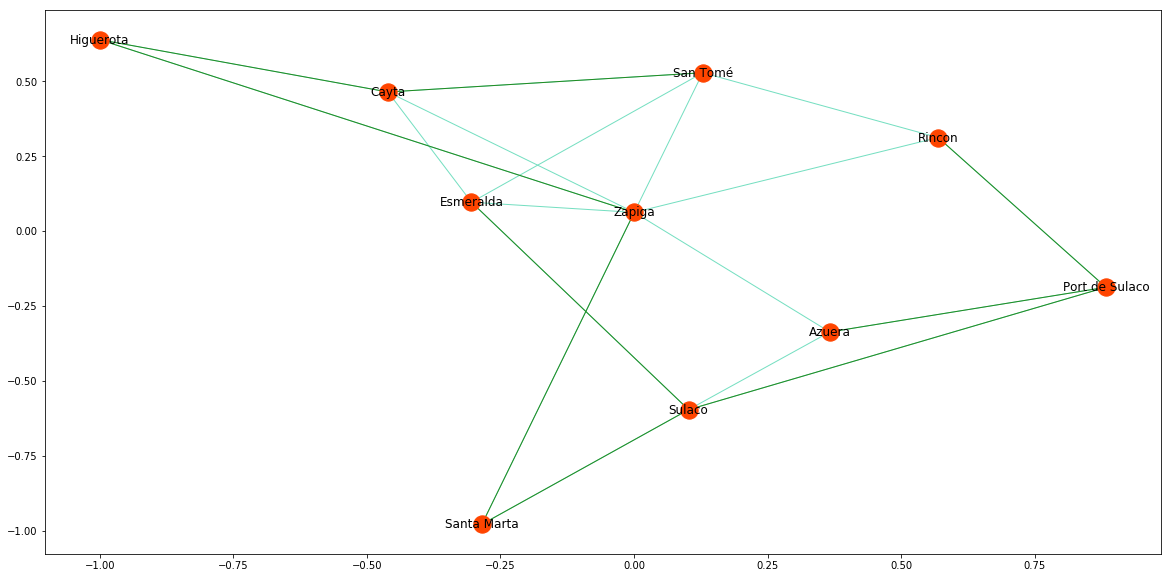
Page Rank :
Der Page Rank ist ein Algorithmus, der von Google verwendet wird, um die Popularität von Webseiten zu berechnen: Die Seiten mit der höchsten Punktzahl werden zuerst angezeigt.
Um diese Punktzahl zu messen, stellt man das Web durch einen Graphen dar, dessen Knoten die Webseiten und dessen Kanten die Hyperlinks/Zwischenseiten sind. Das Prinzip ist folgendes: Die anfänglichen Punktzahlen der Graphen sind einheitlich, dann wird der Graph zufällig durchlaufen, indem man zufällig von einer Website zur nächsten springt (man berücksichtigt also nicht die zuvor besuchten Websites), und bei jedem Durchlauf einer Website wird die Punktzahl aktualisiert.
Am Ende des Algorithmus wird die Punktzahl der Websites proportional zur Wahrscheinlichkeit des Durchlaufens sein: Die Websites, die von dem zufälligen Surfer/Wanderer am häufigsten besucht wurden, werden eine hohe Punktzahl haben.
Eines der Hauptprobleme des PageRanks sind seine sehr hohen Berechnungskosten. Ein verwandter Algorithmus, der SimRank, der die Ähnlichkeit zwischen Webseiten berechnet, wird auch von NetworkX implementiert.
Fazit
NetworkX umfasst eine Reihe von effektiven Methoden für ein breites Spektrum von Anwendungen.
Entdecke mehr über seine Anwendungen in der Datenwissenschaft mit unserem Modul Machine Learning und Graphentheorie mit NetworkX in unserem Kurs Data Scientist.