Die Zeitreihenanalyse ist eine entscheidende Methodik in vielen Bereichen, wie z. B. Finanzwesen, Wirtschaft, Meteorologie und Biologie. Schauen wir uns das SARIMAX Modell einmal genauer an.
Unter den verschiedenen verfügbaren Ansätzen sticht das SARIMAX Modell (Seasonal Autoregressive Integrated Moving Average + exogenous variables) als ein leistungsstarkes Werkzeug hervor, mit dem sowohl Trends als auch saisonale Schwankungen in Zeitdaten modelliert und vorhergesagt werden können, während gleichzeitig exogene Variablen in die Analyse einbezogen werden, um die Genauigkeit der Vorhersagen zu verbessern.
In diesem Artikel werden wir in die Grundlagen des SARIMAX Modells eintauchen, seine Schlüsselkomponenten untersuchen und seine praktische Anwendung erforschen.
Die Grundlage: ARIMA-Modell
Um das Wesen des SARIMAX Modells zu erfassen, wollen wir zunächst die Grundlagen des ARIMA-Modells (Autoregressive Integrated Moving Average) erkunden. ARIMA ist eine leistungsstarke statistische Technik zur Modellierung und Vorhersage von Zeitreihen. Es basiert auf drei Schlüsselkomponenten: Autoregression (AR), gleitender Durchschnitt (MA) und Integration (I).
Die Autoregression (AR) berücksichtigt die vergangenen Werte der Zeitreihe, um die aktuellen Werte vorherzusagen. Bei der Autoregression wird eine lineare Regression auf die letzten p Werte der Zeitreihe durchgeführt, um den aktuellen Wert vorherzusagen:
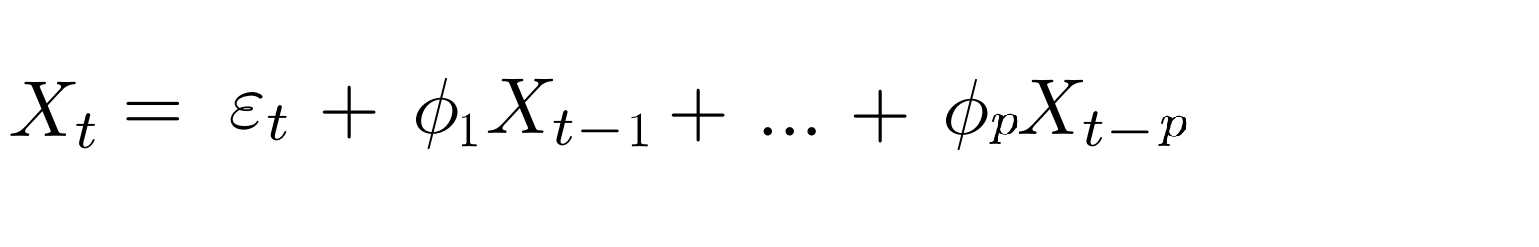
- Der gleitende Durchschnitt (GD) hingegen befasst sich mit vergangenen Fehlern in den Vorhersagen. Er ist durch eine Ordnung gekennzeichnet, die im Allgemeinen mit q bezeichnet wird. Der gleitende Durchschnitt besteht darin, eine lineare Regression auf die letzten q Fehlerwerte durchzuführen, um den aktuellen Wert vorherzusagen:
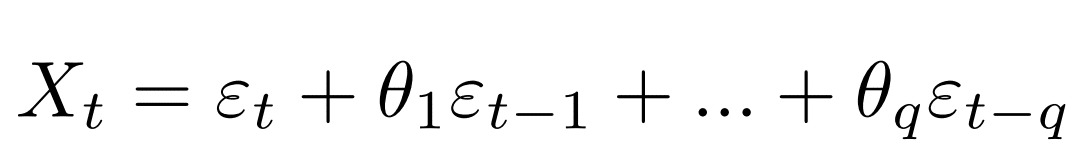
Die Kombination aus Autoregression und gleitendem Durchschnitt bildet das ARMA-Modell. Dieses Modell ist effektiv bei stationären Zeitreihen. Um dies auf eine beliebige Zeitreihe anzuwenden, wird die Integrationskomponente (I) des ARIMA-Modells herangezogen.
- Die Integration (I) greift ein, um die Zeitreihe stationär zu machen, indem die Werte differenziert werden, um die Modellierung zu erleichtern. Die meisten Zeitreihen können nämlich nach einer Reihe von Differenzierungen stationär gemacht werden.
Das ARIMA-Modell wird dann durch drei Koeffizienten charakterisiert: seine Autoregressionsordnung p. Seine Integrationsordnung d, die der Anzahl der Differenzierungen entspricht, die notwendig sind, um die Zeitreihe stationär zu machen. Wenn die Reihe bereits stationär ist, wäre der zu wählende Koeffizient d Null. Seine Ordnung des gleitenden Mittelwerts q.
Nachdem diese Koeffizienten dem ARIMA-Modell gegeben wurden, wird es mit den Daten trainieren, um die optimalen Regressionskoeffizienten in der Autoregression und dem gleitenden Durchschnitt zu finden, um konsistente Vorhersagen zu machen.
Erweiterung zu SARIMA: Ausflug in die saisonalen Schwankungen
Wenn die Zeitdaten saisonale Schwankungen aufweisen, übernimmt das SARIMA-Modell die Szene. Der Begriff „Seasonal“ wird zu ARIMA hinzugefügt, um anzuzeigen, dass dieses Modell Muster erfassen kann, die sich in regelmäßigen Abständen wiederholen.
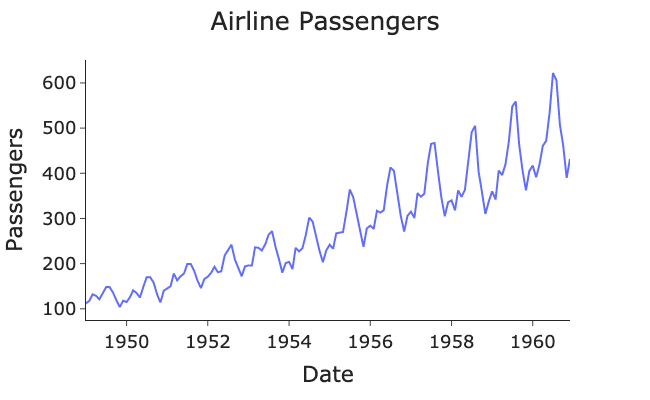
Saisonale Schwankungen können in kurzen Zeiträumen auftreten, wie z. B. bei den monatlichen Verkäufen eines Unternehmens, oder in längeren Zeiträumen, wie z. B. bei Klimadaten. Durch die Einbeziehung einer saisonalen Komponente (S) kann das SARIMA-Modell diese wiederkehrenden Muster modellieren und die Prognosen verbessern. Ein Beispiel für eine nicht-stationäre Zeitreihe mit Saisonalität findest du im folgenden Diagramm, das die jährlichen Passagierzahlen einer Fluggesellschaft darstellt.
Die Revolution: SARIMAX und die Kovariablen
Während das SARIMA Modell bereits eine leistungsstarke Methode zur Modellierung von saisonalen Zeitreihen bietet, kann es auch externe Faktoren geben, die diese Daten beeinflussen. Hier kommt das SARIMAX Modell (Seasonal ARIMA with eXogenous variables) ins Spiel, das die Tür zu einer noch reichhaltigeren Analyse öffnet.
Kovariablen, auch exogene Variablen genannt, sind externe Elemente, die die untersuchte Zeitreihe beeinflussen können. Im Zusammenhang mit den monatlichen Verkäufen eines Unternehmens könnten Kovariablen z. B. Werbeausgaben, besondere Ereignisse oder Feiertage sein. Das SARIMAX Modell ermöglicht es, diese Kovariablen in die Analyse einzubeziehen und so externe Faktoren zu berücksichtigen, die sich auf die beobachteten Trends auswirken können.
Bestandteile des SARIMAX-Modells
Das SARIMAX Modell behält die Schlüsselkomponenten des SARIMA-Modells bei, führt aber zwei wichtige Elemente ein: die Kovariaten (X) und die Komponente der Kovariaten (Z).
- Autoregression (AR): Wie zuvor untersucht die Autoregression die vergangenen Werte der Zeitreihe, um die aktuellen Werte vorherzusagen.
- Gleitender Durchschnitt (GD): Der gleitende Durchschnitt modelliert weiterhin vergangene Fehler in den Vorhersagen.
- Integration (I): Die Integration ist weiterhin vorhanden, um die Zeitreihe stationär zu machen.
- Saisonale Komponente (S): Die saisonale Komponente erfasst Veränderungen, die sich in regelmäßigen Abständen wiederholen.
- Kovariablen (X): Kovariaten sind externe Variablen, die die Zeitreihe beeinflussen können.
- Kovariaten-Komponente (Z): Mit der Kovariatenkomponente wird die Wirkung der Kovariaten auf die Zeitreihe modelliert.
Bestandteile des SARIMAX-Modells
Betrachten wir eine konkrete Anwendung des SARIMAX Modells, um seine Nützlichkeit besser zu verstehen. Angenommen, wir haben monatliche Daten über die Verkäufe eines Unternehmens sowie Daten über die monatlichen Werbeausgaben als Kovariablen.
- Analyse der Daten : Vor der Erstellung des Modells ist es entscheidend, Trends, saisonale Muster und den potenziellen Einfluss der Kovariablen auf die Verkäufe zu analysieren. Dies ist der Schritt der Datenexploration und des Pre-Processing.
- Modellkonstruktion: Durch die Wahl der ARIMA-Ordnungen (p, d, q) und der saisonalen Periode (s) passen wir das SARIMAX Modell unter Berücksichtigung der Kovariablen (in diesem Fall der Werbeausgaben) an.
- Validierung und Prognose: Bewerte die Leistung des Modells, indem du es in einem Zeitraum testest, der sich von dem des Trainings unterscheidet. Metriken wie der mittlere quadratische Fehler (RMSE) geben uns einen Einblick in die Qualität der Vorhersagen. Sobald das Modell validiert ist, kann es für zukünftige Prognosen verwendet werden.
Vorteile von SARIMAX mit Kovariablen
Die Einbeziehung von Kovariablen verleiht dem SARIMAX-Modell einen bedeutenden Vorteil. Durch die Einbeziehung exogener Variablen berücksichtigen die Prognosen nicht nur interne und saisonale Trends, sondern auch externe Faktoren, die die Zeitreihe beeinflussen können. Dadurch können die Entscheidungsträger fundiertere Maßnahmen ergreifen.

Fazit
Das SARIMAX Modell stellt einen bedeutenden Fortschritt in der Zeitreihenanalyse dar, da es die Integration von Kovariablen ermöglicht.
Durch die Einbeziehung externer Variablen zur Bereicherung der Analyse ermöglicht uns dieses Modell ein besseres Verständnis von Trends und zukünftigen Vorhersagen. Wie bei jeder Methodik ist es jedoch entscheidend, die Parameter des Modells zu beherrschen und die Ergebnisse zu verstehen, um relevante und zuverlässige Vorhersagen zu erhalten.
Das SARIMAX Modell mit Kovariablen ist ein wertvoller Beitrag zum Werkzeugkasten der Zeitreihenanalysten und bietet einen umfassenderen Ansatz zur Modellierung und Vorhersage von Daten, die von externen Faktoren beeinflusst werden.
Ob es darum geht, den Umsatz eines Unternehmens zu prognostizieren, Schwankungen auf den Finanzmärkten vorherzusagen oder Klimaschwankungen zu verstehen – das SARIMAX Modell ebnet den Weg für genauere Analysen und fundierte Entscheidungen.
Indem sie die leistungsstarken Fähigkeiten des Modells zur Integration von Kovariablen nutzen, können Fachleute eine ganzheitlichere Perspektive auf zeitliche Trends und die ihnen zugrunde liegenden Faktoren gewinnen. Letztendlich führt das SARIMAX Modell die Zeitreihenanalyse zu neuen Horizonten und verbessert unsere Fähigkeit, komplexe zeitliche Verhaltensweisen zu interpretieren und zu antizipieren.