Today, we present the 4th installment of our exciting NLP dossier.
In this article, we'll look at how to build a translation algorithm on Python -machine translation in English- that translates any word from a source language into a target language from words embeddings.
Implémenter ce genre d’algorithme peut paraître, au premier abord, un peu flou. Mathématiquement, cela revient à trouver la matrice de correspondance (ou matrice d’alignement) W résolvant le problème d’optimisation suivant :
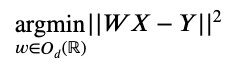
Where :
- Od(R) is the set of orthogonal matrices (i.e. the set of M matrices with real coefficients, invertible and such that 𝑀-1=𝑀T ).
- X and Y are respectively the matrices containing the embeddings of transparent words (e.g. table, television, radio, piano, telephone, etc.) present in the source language (French) and in the target language (English).
- X and Y are thus called the French and English word embedding matrices respectively.
Transparent words will be essential to the construction of the translation algorithm, in that they correspond to reference points for aligning the two embedding vector spaces after application of the alignment matrix W. In other words, transparent words will make it possible to determine the existing geometric transformation between the two subspaces. In other words, the transparent words determine the geometric transformation between the two subspaces.
By the way, what is an embedding matrix?
To explain what an embedding matrix is, let’s take the following three sentences:
- When the worker left.
- When the fisherman left.
- When the dog left.
Let’s imagine that we don’t know the meaning of the words ‘worker’, ‘fisherman’ and ‘dog’, but we’re able to say that these three sentences are identical except for one word. As the contexts are similar, we could deduce that there is a certain similarity between ‘worker’, ‘fisherman’ and ‘dog’.
Applying this idea to an entire corpus, we could define relations between several words in this way.
However, the question remains: how best to represent these relationships? This is where the concept of the embedding matrix comes in.
For the sake of simplicity, let’s imagine that each word and its meaning can be represented in an abstract three-dimensional space.
Conceptually, this means that all words exist as singular points in a 3D space, and any word can be uniquely defined by its position in this space described by three numbers (x, y, z).
In reality, however, the meaning of a word is too complicated to be simply described in a three-dimensional space, and as a general rule it takes almost 300 dimensions to fully define a word and its meaning.
The vector of 300 numbers that identifies a given word is called the embedding of that word.
Ultimately, an embedding matrix is nothing more than a matrix containing a wide variety of words and their corresponding embeddings. Below is an example of an English embedding matrix:

Implémentation d’un algorithme de traduction et ses limites
In this section, we will implement a translation algorithm and try to determine both its strengths and weaknesses.
Step 0:
Recovery of two embedding matrices U1 and U2 respectively French and English pre-trained on Common Crawl and Wikipedia using fastText.

Step 1:
First, we need to define a bilingual dictionary (e.g. French-English) containing all the transparent words contained in both vocabularies. Once this has been obtained, we need to construct the embedding matrices X and Y corresponding respectively to the French and English matrices containing the embeddings associated with the words in the previously defined bilingual dictionary.
Step 2:
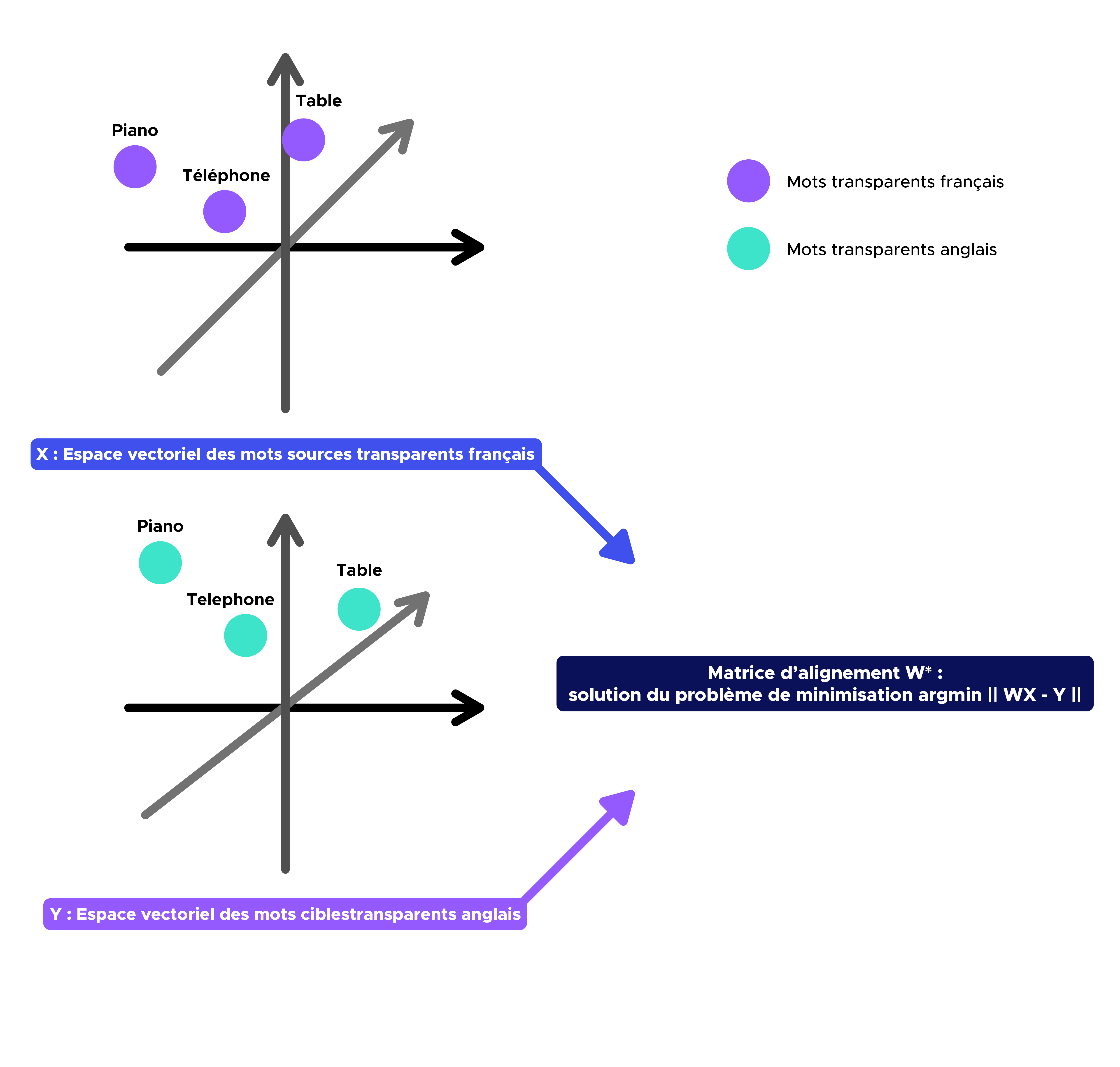
The aim of this second step is to find the W application (correspondence matrix) that will project the source word vector space (e.g. French) onto the target word vector space (e.g. English).
Obviously, the more similar the structure of the embedding spaces, the more efficient this method will be (which is the case here with French and English).
As we saw in the preamble, W* = argmin || WX – Y || under the constraint that W is an orthogonal matrix.
Using orthogonality and the properties of the trace of a matrix, we can prove that
W*=UVT with UΣVT = SVD (YXT)
Where SVD is the singular value decomposition of a matrix (a generalization of the spectral theorem which states that all orthogonal matrices can be diagonalized by an orthonormal basis of eigenvectors).
Given the previous result, finding W is simply a matter of singular-value decomposition of the matrix 𝑌𝑋T.
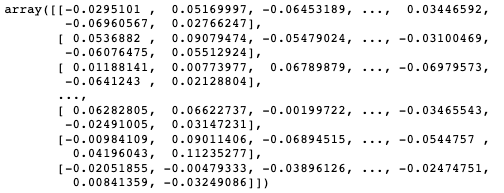
Here is the W matrix obtained as code output:
Step 3:

Once the W alignment matrix has been obtained, we can now find the English translation of any word in the French vocabulary by identifying the source words’ nearest neighbors in the target word vector space.
Here are the results (each time, 3 English terms closest to the translation and their probability of correspondence with the word to be translated):

As we can see, this algorithm is quite powerful and can be used as a French-English word translator.
We could try using this kind of algorithm to translate an entire text:
Here is the result
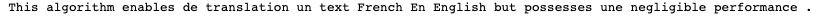
Given the difference in linguistic structure between French and English (e.g. noun-adjective order in French, adjective-noun order in English), word-to-word translation is not optimal. What’s more, we can see that our translation algorithm doesn’t work for words such as: de, en, un, une, etc.
As we suspected, word-for-word translation is not the most efficient way to translate a text. One possible solution is to use a Seq2seq (or BERT) approach, which will be the subject of a forthcoming article.
Did you like this article?
Would you like to learn more about Deep Learning?










