Aujourd’hui, nous allons vous présenter le 4ème volet de notre passionnant dossier NLP.
Dans cet article, nous allons voir comment construire un algorithme de traduction sur Python -machine translation en anglais- permettant de traduire tout mot provenant d'une langue source vers une langue cible à partir des words embeddings.
Vous avez raté les premiers épisodes ? Pas de panique les voici :
Implémenter ce genre d’algorithme peut paraître, au premier abord, un peu flou. Mathématiquement, cela revient à trouver la matrice de correspondance (ou matrice d’alignement) W résolvant le problème d’optimisation suivant :
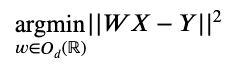
Où :
- Od(R) est l’ensemble des matrices orthogonales (i.e. l’ensemble des matrices M à coefficients réelles, inversibles et tel que 𝑀-1=𝑀T ).
- X et Y sont respectivement les matrices contenant les embeddings des mots transparents (par exemple, table, television, radio, piano, telephone, etc.) présents dans la langue source (français) et dans la langue cible (anglais). X et Y sont ainsi appelées respectivement les matrice d’embeddings des mots français et anglais
Les mots transparents vont être essentiels à la construction de l’algorithme de traduction au sens où ils correspondent à des points de repère permettant d’aligner les deux espaces vectoriels d’embeddings après application de la matrice de d’alignement W. Autrement dit, les mots transparents vont permettre de déterminer la transformation géométrique existante entre les deux sous-espaces vectoriels.
Au fait, qu’est ce qu’une matrice de embeddings ?
Pour expliquer ce qu’est une matrice de embeddings, prenons les trois phrases suivantes :
- Lorsque l’ouvrier est parti.
- Lorsque le pêcheur est parti.
- Lorsque le chien est parti.
Imaginons que nous ne connaissons pas la signification des mots ‘ouvrier’, ‘pêcheur’ et ‘chien’, nous sommes toutefois capable de dire que ces trois phrases sont identiques à l’exception d’un mot. Les contextes étant similaires, nous pourrions déduire qu’il existe une certaine similitude entre ‘ouvrier’, ‘pêcheur’ et ‘chien’. En appliquant cette idée à un corpus entier, nous pourrions définir ainsi les relations entre plusieurs mots. Toutefois, une question subsiste : comment représenter au mieux ces relations ? C’est ainsi qu’apparaît le concept de matrice d’embeddings.
Par soucis de simplicité, imaginons que chaque mot et sa signification puissent être représentées dans un espace abstrait de trois dimensions.
Conceptuellement, cela signifie que tous les mots existent en tant que points singuliers dans un espace 3D et n’importe quel mot peut être défini de manière unique par sa position dans cet espace décrit par trois nombres (x, y, z).
Toutefois, en réalité, le sens d’un mot est trop compliqué pour être simplement décrit dans un espace de trois dimensions et en règle générale, il faut près de 300 dimensions pour définir complètement un mot et sa signification.
Le vecteur de 300 nombres qui identifie un mot donné est appelé l’embedding de ce mot.
Finalement, une matrice d’embeddings n’est rien d’autre qu’une matrice contenant une grande variété de mots et leurs embeddings correspondants. Voici ci-dessous, un exemple de matrice d’embeddings anglais :

Implémentation d’un algorithme de traduction et ses limites
Nous allons dans cette section implémenter un algorithme de traduction et essayer de déterminer à la fois ses forces et ses faiblesses.
Étape 0 :
Récupération de deux matrices d’embeddings U1 et U2 respectivement françaises et anglaises pré-entraîné sur Common Crawl et Wikipedia à l’ aide de fastText.
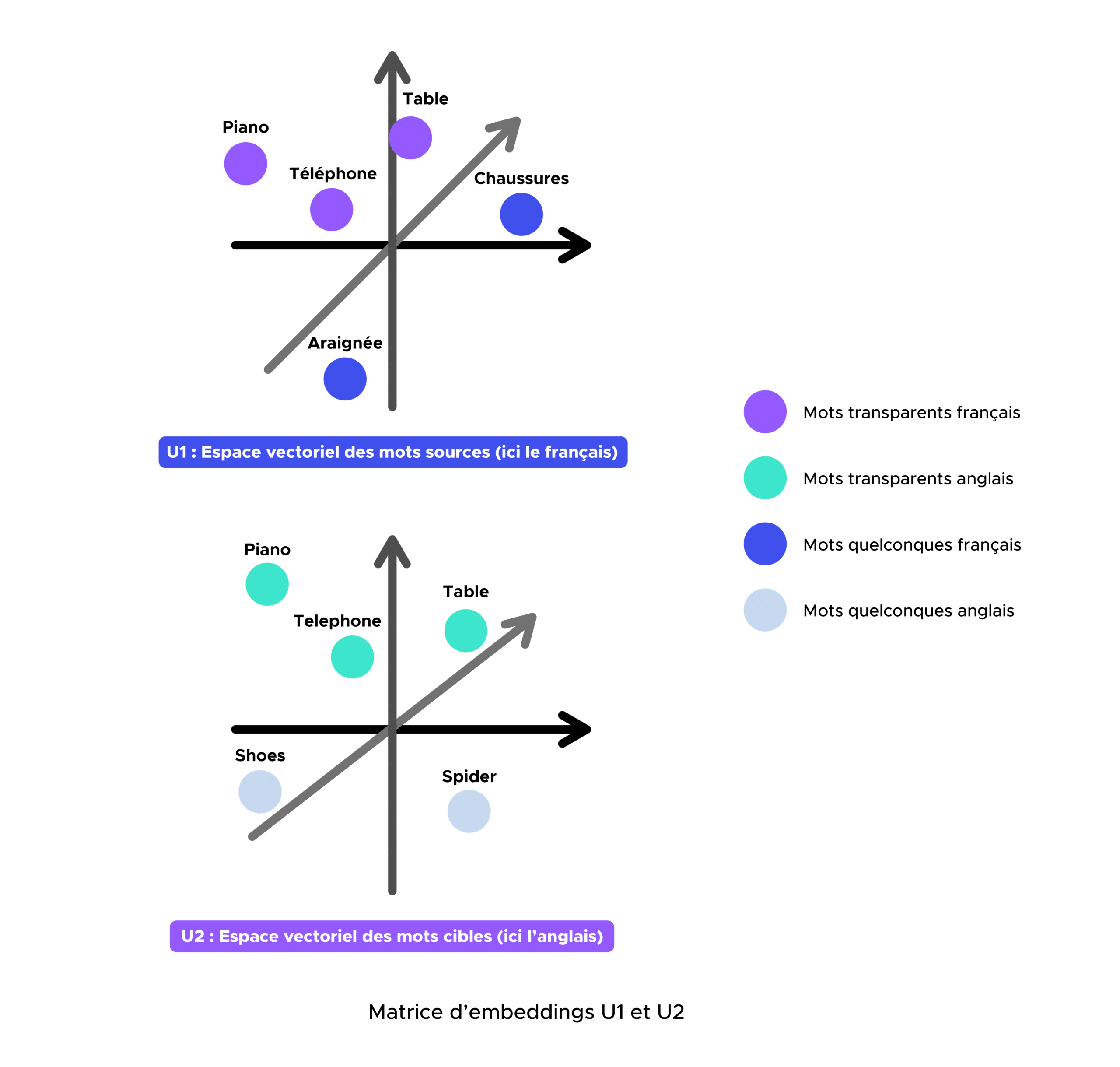
Étape 1 :
Dans un premier temps, nous devons définir un dictionnaire bilingue (par exemple français-anglais) contenant tous les mots transparents contenus dans les deux vocabulaires. Une fois ce dernier obtenu, nous devons construire les matrices d’embeddings X et Y correspondant respectivement aux matrices françaises et anglaises contenant les embeddings associés aux mots du dictionnaire bilingue précédemment défini.
Étape 2 :
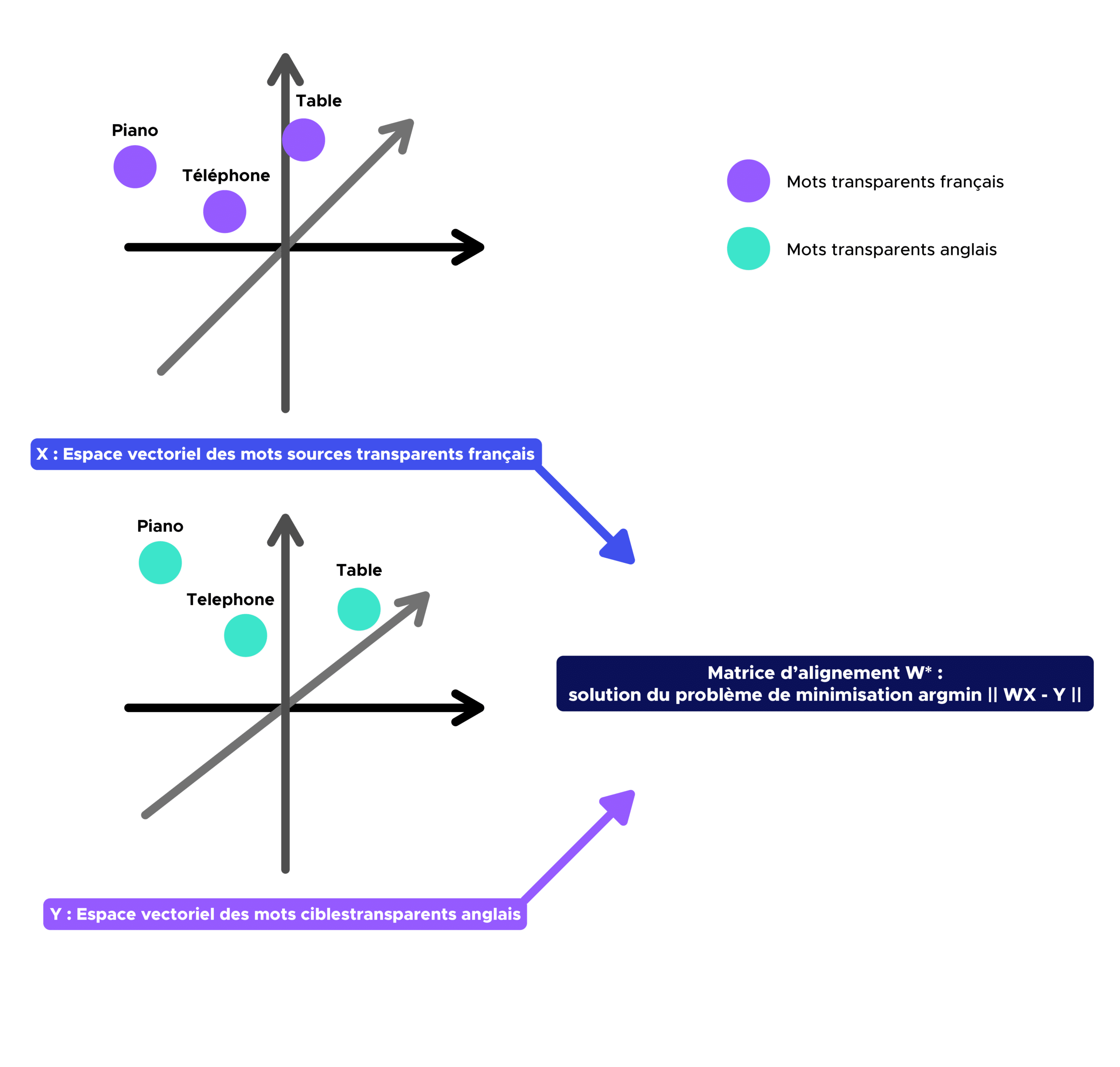
L’objectif de cette deuxième étape est de trouver l’application W (matrice de correspondance) qui projettera l’espace vectoriel de mots source (par exemple le français) sur l’espace vectoriel de mots cible (par exemple l’anglais).
Evidemment, plus la structure des espaces d’embeddings sera similaire, plus cette méthode sera performante (ce qui est le cas ici avec le français et l’anglais).
Comme nous l’avons vu en préambule, W* = argmin || WX – Y || sous la contrainte que W soit une matrice orthogonale.
Nous pouvons prouver en utilisant l’orthogonalité et les propriétés de la trace d’une matrice que
W*=UVT avec UΣVT = SVD (YXT)
Où SVD est la décomposition en valeur singulière d’une matrice (généralisation du théoreme spectral qui énonce que toutes matrices orthogonales peuvent être diagonalisées par une base orthonormée de vecteurs propres).
Fort du résultat précédent, trouver W revient simplement à décomposer en valeur singulière la matrice 𝑌𝑋T.
Voici la matrice W obtenue en sortie de code :

Étape 3 :
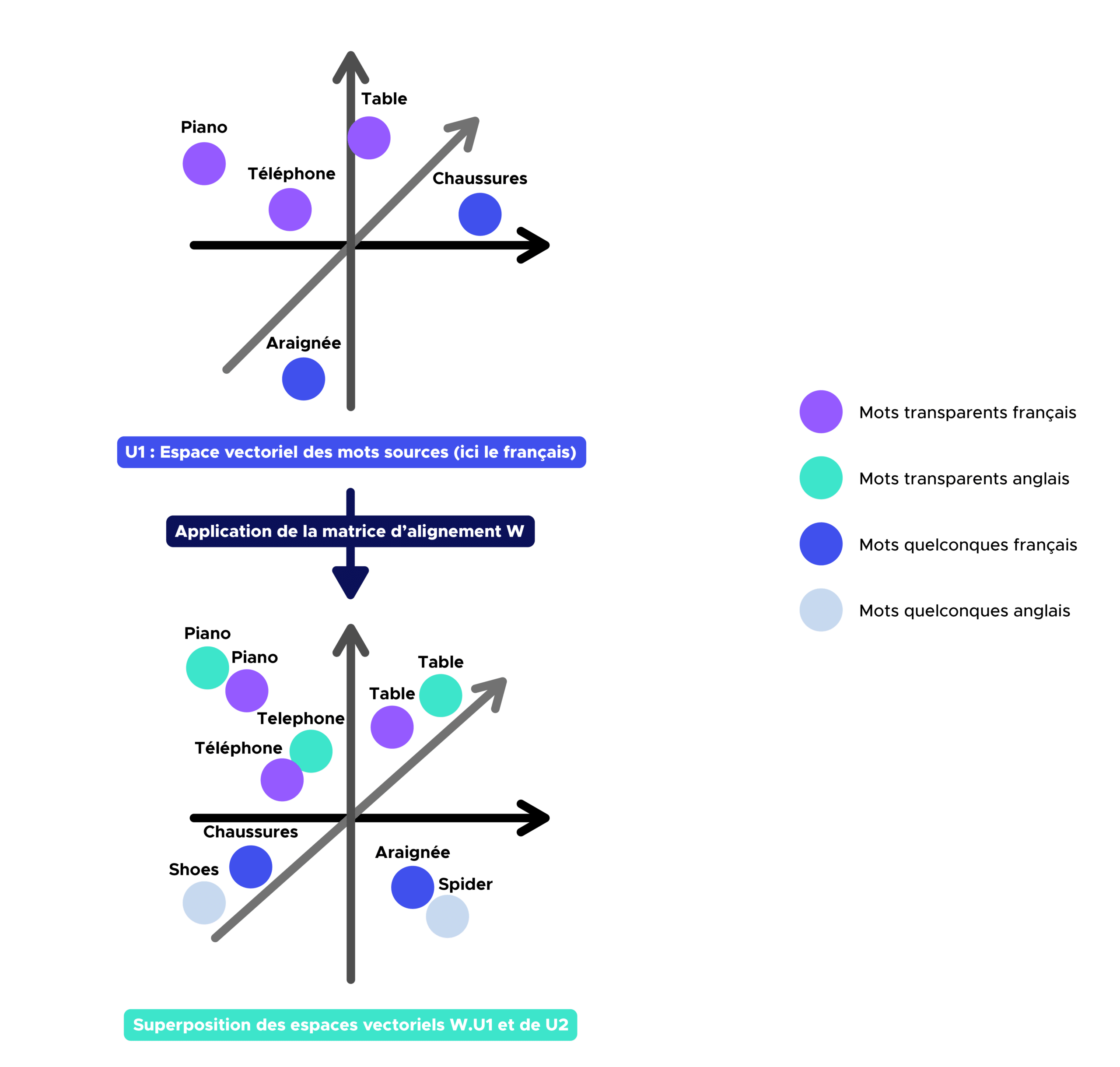
Une fois la matrice d’alignement W obtenue, nous pouvons désormais trouver la traduction en anglais de n’importe quel mot présent dans le vocabulaire français en identifiant les plus proches voisins des mots sources dans l’espace vectoriel de mots cible.
Voici les résultats obtenues (à chaque fois, 3 termes anglais les plus proches de la traduction et leur probabilité de correspondance avec le mot à traduire) :

Comme nous pouvons le constater, cet algorithme est assez performant et peut servir de traducteur de mots français-anglais.
Nous pourrions essayer d’utiliser ce genre d’algorithme pour traduire tout un texte :
Voici le résultat obtenu
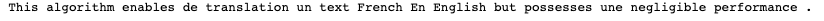
Compte tenu de la différence de structure linguistique entre le français et l’anglais (par exemple l’ordre nom-adjectif en français, adjectif-nom en anglais), la traduction mot à mot n’est pas optimale. De plus, nous pouvons remarquer que notre algorithme de traduction ne fonctionne pas pour les mots tels que : de, en, un, une, etc.
Comme nous pouvions nous en douter, la traduction mot à mot n’est pas la méthode la plus performante pour traduire un texte. Une des solutions possibles serait d’utiliser une approche Seq2seq (ou BERT) dont un prochain article lui sera prochainement consacré.
Cet article vous a plu ?
Vous aimeriez aller plus loin en Deep Learning ?










