On a traité dans un précédent article de l’importance des algorithmes de recherche de plus court chemin en théorie des graphes, notamment avec l’exemple de l’algorithme de Dijkstra. Il existe d’autres algorithmes encore plus performants dans certaines situations, comme en cartographie ou dans le gaming. On retient par exemple l’algorithme A*, dit ‘A star algorithm’ en anglais. Découvrons son fonctionnement dans cet article :
L’algorithme A* est un algorithme heuristique qui permet de trouver très rapidement un plus court chemin entre deux points avec d’éventuels obstacles. Outre sa vitesse, cet algorithme est réputé pour garantir une solution en sortie.
NB : Un algorithme heuristique est un procédé qui permet d’obtenir une solution réalisable très rapidement à un problème d’optimisation complexe. La solution fournie en sortie de l’algorithme n’est cependant pas garantie d’être optimale.
Comment fonctionne-t-il ?
Illustrons le fonctionnement de cet algorithme par un exemple :
Un individu cherche à se déplacer d’un point A à un point B sur un chemin d’obstacles.
La situation est représentée par les schémas ci-dessous :

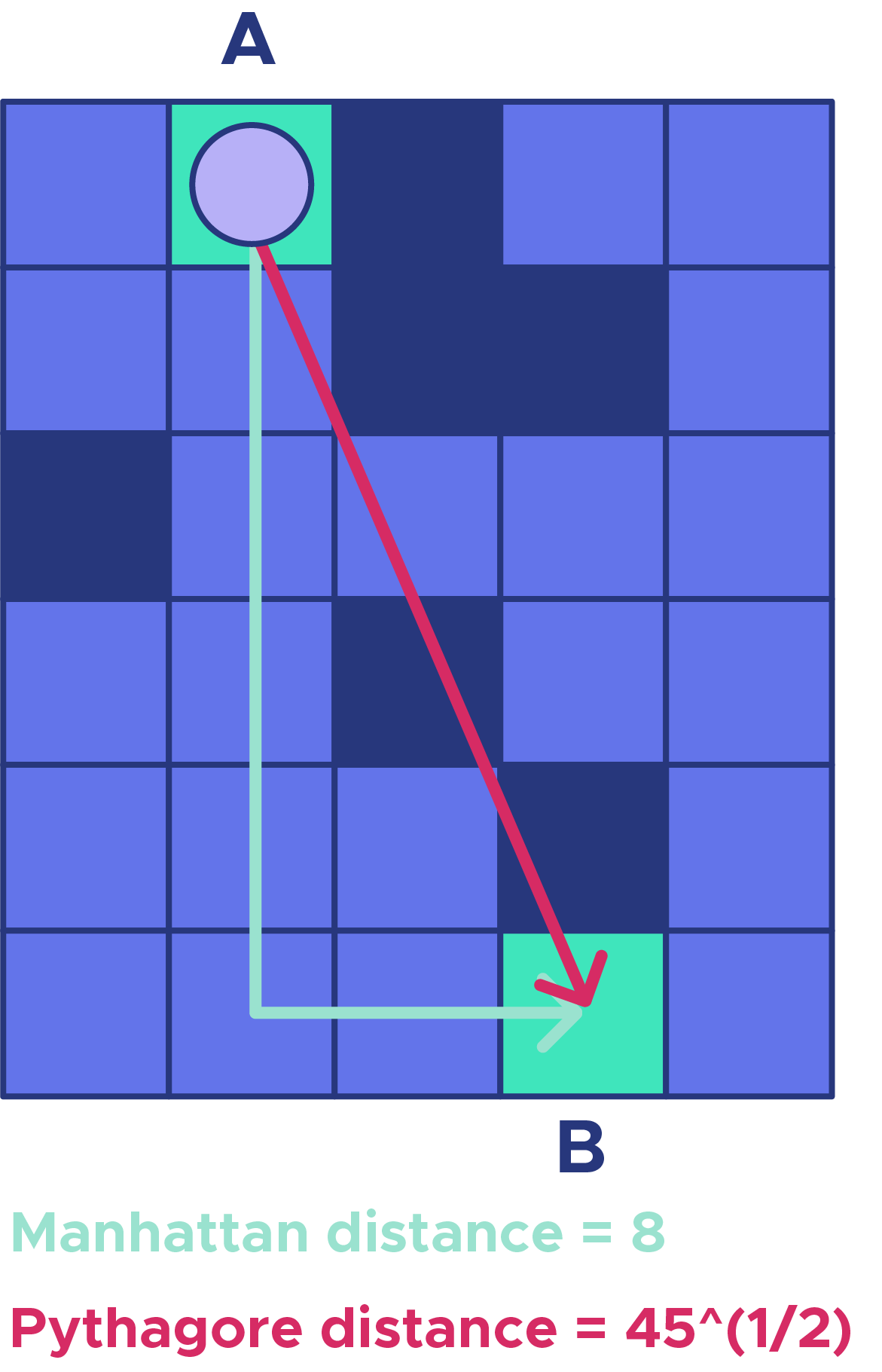
Les cases vertes représentent le point de départ et l’arrivée. Les cases foncées représentent les obstacles, et les bleues celles où il est possible de se déplacer. Sur le schéma numéro 2, les cases violet claires représentent un chemin théorique éligible pour modéliser l’heuristique, aussi représenté avec la flèche verte.
L’enjeu ici est de trouver le plus court chemin menant à B, l’individu ne pouvant pas emprunter les cases noires.
Un algorithme heuristique traditionnel évaluerait tous les chemins possibles et comparerait leur distance, tandis que l’algorithme A* nous renvoie directement le premier chemin qu’il a déterminé.
Le caractère optimal de ce chemin dépendra du paramètre d’heuristique choisi. Dans notre cas, l’heuristique sert à fournir une estimation de la distance restante à chaque étape de l’algorithme. Cette estimation dépend de la métrique choisie dans notre problème d’optimisation, et n’a pas à rendre une distance exacte.
Dans notre cas, on pourrait choisir comme heuristique la distance de Manhattan séparant A et B, ou la distance en ligne droite entre ces deux points, calculée à l’aide du théorème de Pythagore.
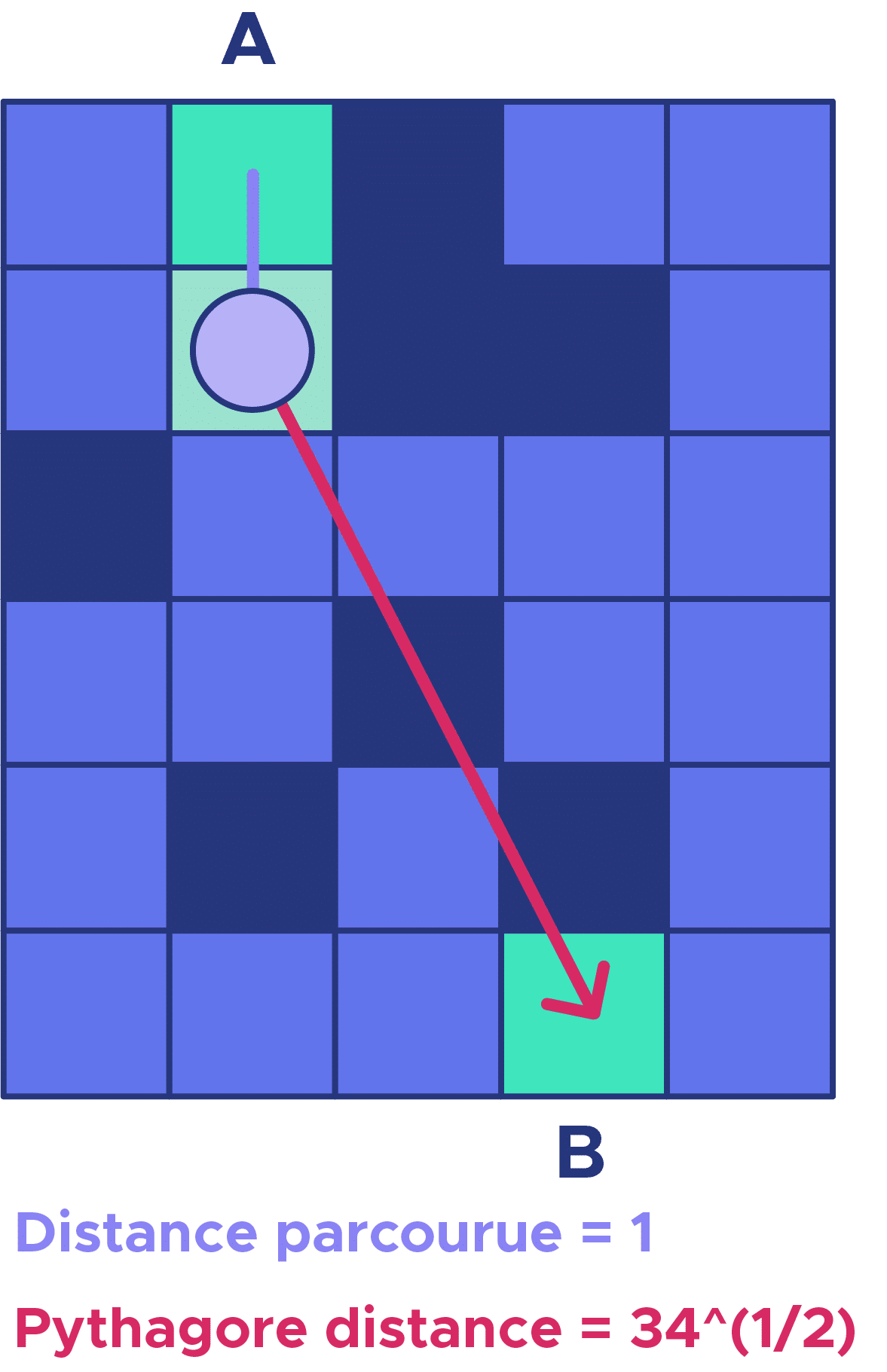
L’algorithme A* essaye par conséquent de minimiser la somme F = G+H, où G est la distance parcourue depuis le point de départ et H l’estimation de la distance restante à parcourir jusqu’à l’arrivée, en fonction de l’heuristique définie au départ de l’algorithme. Ainsi, en entrée, l’algorithme prend :
- Les positions des points de départ et d’arrivée
- La liste des distances entre chaque case de la grille et le point d’arrivée.
A chaque étape, l’algorithme A* met ainsi à jour deux listes :
- Celle des grandeurs G, représentant la distance réelle parcourue depuis le point A
- Celle des estimations H décrivant la distance à parcourir jusqu’à l’arrivée.
Ainsi, l’algorithme choisit à chaque étape la case lui permettant de se rapprocher de l’arrivée, et stocke dans une autre liste d’autres options moins optimales aux premiers abords.
Cette liste secondaire permet de choisir une autre option au cas où l’algorithme rencontre un obstacle, ce qui garantit la justesse de l’algorithme.
Le choix de l’heuristique d’estimation est crucial pour l’optimalité du chemin renvoyé. Si l’on surestime le chemin restant à parcourir à chaque étape, l’algorithme risque de ne pas renvoyer le chemin le plus court. En revanche, si l’on sous-estime l’heuristique, la complexité de l’algorithme augmentera, ce qui lui fera perdre son atout principal qu’est sa vitesse (l’heuristique nulle représente l’algorithme de Dijsktra). Si l’estimation est juste, l’algorithme n’explorera pas toutes les options possibles et renverra une solution optimale. On dit dans ce cas que l’heuristique fournie est admissible.
Cet article vous a plu ? Notre formation data scientist vous propose un cours sur la théorie des graphes, pour que vous puissiez, vous aussi, comprendre et implémenter un tel algorithme sur Python.