Lorsqu’on débute un projet de Data Science, il est très important de réfléchir à la modélisation du problème en question.
Si l’on cherche à augmenter les ventes sur un site de e-commerce, on peut chercher à augmenter les taux de conversion avec un modèle de classification, déterminer la durée de visite des utilisateurs en fonction de leur profil, modéliser le parcours des visiteurs, attribuer aux différents canaux marketing la venue des visiteurs, améliorer le référencement du site…
On a alors différentes approches mathématiques possibles: Machine Learning, analyse de survie, chaînes de Markov, calcul des valeurs de Shapley, estimation d’un score PageRank, …

On voit alors que le Machine Learning n’est pas l’Alpha et l’Oméga du métier de Data Scientist et qu’il faut s’intéresser à des modèles mathématiques autres qui reposent sur la théorie des probabilités, la théorie des jeux ou la théorie des graphes.
C’est dans cette optique que nous allons développer un cours, sur un sujet, tristement d’actualité, l’Analyse de Survie.

L’analyse de survie qu’est-ce que c’est ?
L’analyse de survie est un champs des statistiques qui s’intéresse à la durée de vie des individus au sein d’une population. On essaie d’y estimer la date à laquelle survient un décès.
Mais son champ d’application est bien plus vaste:
- maintenance prédictive: prédire la date de panne d’une machine pour pouvoir intervenir à temps
- churn analysis: prédire la date à laquelle un client va se désabonner d’un service
- credit analysis: prédire la date à laquelle un client va être en défaut
- epidémiologie: prédire la date à laquelle un patient sera guéri (c’est alors le virus/la bactérie qui meurt)
L’utilisation de ce genre de modèles remonte aux années 1950 en médecine mais certains chercheurs travaillent sur des algorithmes qui allient cette modélisation à des techniques de Machine Learning.
Zoom sur la fonction de survie
En analyse de survie, on cherche à estimer la distribution d’une variable aléatoire X qui correspond à la date de décès. On introduit alors la fonction de survie:
S(t) = P(X>t)
et le taux de risque instantané :
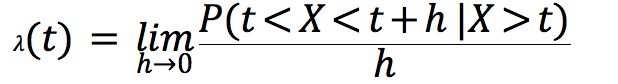
On va pouvoir estimer ces quantités en utilisant des estimateurs non-paramétriques (Kaplan-Meier), semi-paramétriques (Cox) ou paramétriques. Ces deux derniers types d’estimateurs permettent notamment de mesurer l’influence de variables explicatives sur la fonction de survie.
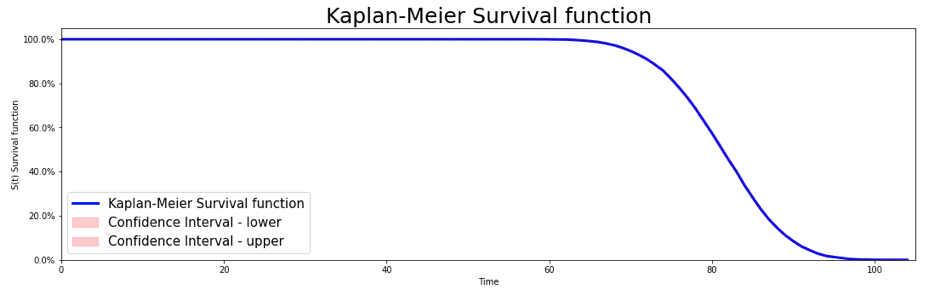
En analyse de survie, la librairie PySurvival est très utile , elle est très bien référencée et documentée et propose beaucoup d’outils intéressants de visualisation et de mesure des performances.
Cet article vous a mis l’eau à la bouche? Sachez qu’une formation sur le sujet démarre bientôt ! N’hésitez pas à nous contacter pour plus d’infos !
Vous souhaitez en apprendre davantage sur toutes les possibilités du Machine Learning ? Démarrez l’une de nos formations !









