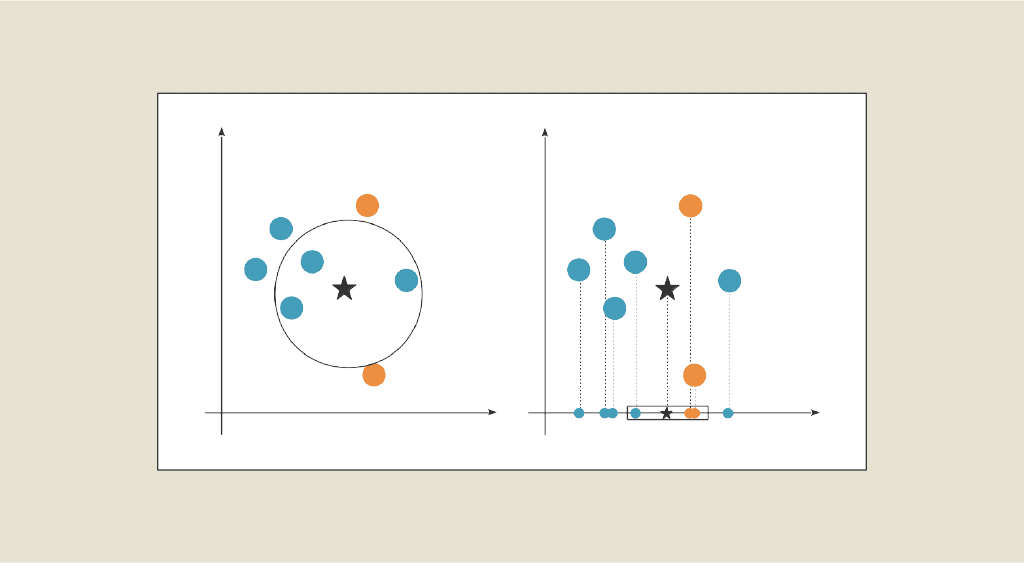
L’analyse de données peut être considérée comme une science expérimentale, où les propriétés sont démontrées après avoir été observées, et où des codes sont établis de manière heuristique pour interpréter les résultats. Dans le domaine de l’apprentissage automatique (machine learning) et de l’analyse des données, la réduction de dimension joue un rôle essentiel pour simplifier les ensembles de données complexes.
L’idée de base de la réduction de dimension consiste à représenter des données multidimensionnelles dans un espace de dimension bien inférieure tout en conservant les informations importantes et pertinentes.
Avant de se plonger dans plus de détails mathématiques, il est important de comprendre certains termes clés.
Le vocabulaire de la réduction de dimension
- L’espace de dimension : nombre de caractéristiques ou variables qui décrivent un objet dans un dataset. Par exemple, une base de données rassemblant des caractéristiques sur des personnes peut comporter des variables telles que l’âge, le revenu, l’adresse, le sexe, et le niveau d’éducation. Ceci définit un espace de dimension cinq.
- La projection consiste à transformer les données d’un espace de dimension élevée vers un espace de dimension réduite en utilisant des techniques de réduction de dimension. Cette transformation permet de représenter les données de manière plus compacte tout en conservant les informations importantes.
- L’orthogonalité est une propriété mathématique dans laquelle deux vecteurs ou deux espaces sont perpendiculaires les uns aux autres. Dans le contexte de la réduction de dimension, l’orthogonalité est souvent utilisée pour décrire des variables ou des composantes qui sont décorrélées les unes des autres.
Si les données sont représentées dans un tableau, la réduction de dimensionnalité passe par une diminution du nombre de colonnes. Si notre dataset est composé de plus de 3 variables, plus la dimension augmente, plus il est difficile de le visualiser. Ainsi, ce n’est pas possible de visualiser un jeu de données à 13 attributs mais cela est possible avec seulement 2 ou 3 attributs. L’objectif est donc de projeter ces données sur les 2 ou 3 axes les plus importants en termes de contenu d’information afin de garder la représentation des données la plus proche de celles en grande dimension.
Un exemple très simple : Supposons que nous ayons un jeu de données contenant des informations sur des étudiants, comprenant les 5 variables suivantes et chaque étudiant est représenté par une ligne dans le jeu de données, chaque variable correspondant à une colonne.
| Etudiant | Âge | Taille | Poids | Maths | Sciences |
|---|---|---|---|---|---|
| Etudiant 1 | 18 | 165 | 60 | 85 | 90 |
| Etudiant 2 | 20 | 170 | 65 | 75 | 80 |
| Etudiant 3 | 19 | 175 | 70 | 90 | 95 |
| Etudiant 4 | 22 | 180 | 75 | 80 | 70 |
Après application de l’ACP pour réduire la dimension, nous pourrions obtenir un nouvel ensemble de données avec moins de variables, par exemple, en conservant uniquement les deux premières composantes principales. On obtiendrait le jeu de données suivant :
| Etudiant | Composante Principale 1 | Composante Principale 2 |
|---|---|---|
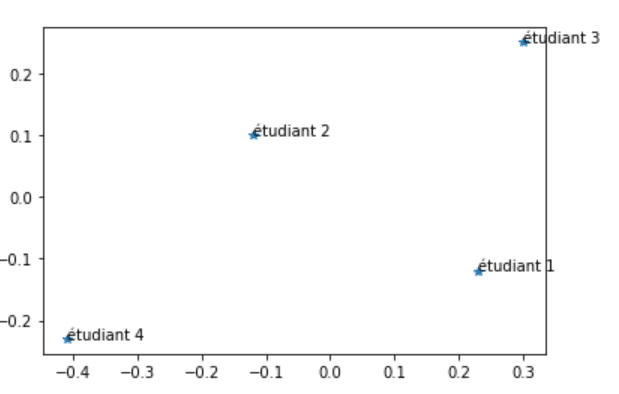
| Etudiant 1 | 0.23 | -0.12 |
| Etudiant 2 | -0.12 | 0.10 |
| Etudiant 3 | 0.30 | 0.25 |
| Etudiant 4 | -0.41 | -0.23 |
Ainsi, cet ensemble de données est facilement représentable sur un graphique en 2 dimensions :
En savoir plus sur l'Analyse en Composantes Principales (ACP)
- On calcule la matrice de covariance de X, que l’on note C. Cette matrice mesure les relations linéaires entre les variables. Elle est calculée grâce à la formule suivante : C = 1/nXT X
- Nous cherchons les vecteurs propres de la matrice de covariance C. Les vecteurs propres sont des directions dans l’espace des variables qui décrivent la variance des données. Les vecteurs propres sont normalisés afin que leur norme soit égale à 1.
- Nous ordonnons ces vecteurs propres par ordre décroissant de leur valeur propre associée : ν1 associé à λ1, ν2 associé à λ2 et λ1≥λ2 et ainsi de suite. Plus la valeur propre est élevée, plus la variance expliquée par la direction correspondante est grande.
- On choisit un nombre k de composantes principales (souvent 1, 2 ou 3) à conserver et on sélectionne les k premiers vecteurs propres (ν1, ν2, … , νk). Ces vecteurs propres forment une base orthonormale dans le nouvel espace de dimension réduite. Ainsi, les nouvelles variables créées sont décorrélées. On note W la matrice formée par ces k premiers vecteurs propres.
- On veut maintenant projeter nos données dans ce nouvel espace, dont une base est composée des vecteurs (ν1, ν2, … , νk). Pour projeter les données originales dans cet espace de dimension réduite, nous utilisons la transformation linéaire suivante : Y = XW, où Y correspond aux coordonnées de nos données suite à la projection.
Pour plus de détails sur l’ACP, vous pouvez lire notre article dédié spécifiquement à cette méthode.
Il existe d’autres méthodes de réduction de dimension, les plus connues restent :
- LDA (linear discriminant analysis) : l’analyse discriminante linéaire qui permet d’identifier les directions décorrélées les unes des autres. Elle vise à trouver une projection linéaire des données qui maximise la séparation entre les classes tout en minimisant la variance intraclasse.
- T-SNE (t-Distributed Stochastic Neighbor Embedding) : T-SNE est une méthode non linéaire de réduction de dimension permettant de représenter des données de haute dimension dans un espace de dimension réduite (typiquement 2D ou 3D). Pour plus de détails à ce sujet, lisez cet article. Le t-NSE est particulièrement adapté à la visualisation des structures complexes et des relations non linéaires dans les données.
Limites et difficultés de la réduction de dimension
Il est important de noter que la réduction de dimension est un compromis entre la simplification des données et la perte d’information. En réduisant la dimension, il est possible de perdre certaines informations subtiles ou des détails spécifiques. Par conséquent, il est crucial de trouver le bon équilibre en sélectionnant le nombre approprié de composantes principales capturant la majeure partie de l’information pertinente.
Chaque méthode a ses avantages et ses limites, et le choix de la méthode dépend du contexte spécifique et des objectifs de l’analyse de données.
Si cet article vous a plu, vous pouvez découvrir plus en détail ces méthodes dans nos formations Data Analyst et Data Scientist. N’hésitez pas à les consulter !