Ça y est ! Le jeu de données est nettoyé! Plus de valeurs manquantes, les choix de modélisation ont été faits ! On a gardé certaines variables, on en a supprimé d'autres. Il faut maintenant réaliser la dernière étape avant de faire tourner les algorithmes de Machine Learning: adapter les variables à l'algorithme.
En effet, la plupart des algorithmes de Machine Learning ne permettent pas d’utiliser des variables autres que numériques: à part les arbres de décision et ses dérivés (forêts aléatoires, gradient boosting tree…), les algorithmes de Machine Learning les plus utilisés reposent sur des calculs de distance entre différentes observations.
Dans cet article, nous allons traiter de la manière de préparer les données afin de les fournir à un algorithme de Machine Learning et tenter d’y apporter une justification.
Préparer une variable quantitative
On retrouve très vite des variables quantitatives lorsque l’on fait du Machine Learning : âge d’un client, prix d’une voiture, surface d’un terrain… Il n’y a d’ailleurs finalement que peu de différences entre une variable discrète et une variable continue : les transformations que nous leur faisons subir n’ont pas d’impact sur la qualité de l’information contenue.
Pour préparer une variable quantitative, on utilise une normalisation standard ou min-max. Cette normalisation permet de ramener les valeurs dans un intervalle normalisé: de 0 à 1 pour le min-max et entre -1 et 1 pour la plupart des données pour le standard.
Si une des fonctions principales de la normalisation des données est d’améliorer et d’accélérer la convergence d’algorithmes basés sur la descente de gradient (SVM, régressions…), elle permet aussi de fournir des résultats plus pertinents dans le cadre d’un clustering: dans l’exemple suivant on génère des données aléatoires en essayant de définir des clusters assez visuels et des données un peu plus aberrantes. On entraîne alors un KMeans avec ou sans normalisation :
import numpy as np
import pandas as pd
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
%matplotlib inline
a = np.random.normal(size=100)
a[:50] = a[:50] + 100
a[50] = a[50] + 60
a[51] = a[51] + 40
b = np.random.normal(size=100)
b[25:75] = b[25:75] + 10
b[51] = b[51] - 10
df = pd.DataFrame({'a': a, 'b':b})
df_standard = df.copy(deep=True)
df_minmax = df.copy(deep=True)
df['cluster'] = KMeans(n_clusters=4).fit_predict(df)
df_standard[df_standard.columns] = StandardScaler().fit_transform(df_standard)
df_standard['cluster'] = KMeans(n_clusters=4).fit_predict(df_standard)
df_minmax[df_minmax.columns] = MinMaxScaler().fit_transform(df_minmax)
df_minmax['cluster'] = KMeans(n_clusters=4).fit_predict(df_minmax)
fig, axes = plt.subplots(ncols=3, nrows=2, figsize=(15, 10))
axes[0, 0].scatter(df['a'], df['b'], color='b', alpha=.5)
axes[0, 1].scatter(df_standard['a'], df_standard['b'], color='b', alpha=.5)
axes[0, 2].scatter(df_minmax['a'], df_minmax['b'], color='b', alpha=.5)
axes[0, 0].set_title('No scaler')
axes[0, 1].set_title('Standard scaler')
axes[0, 2].set_title('MinMax scaler')
On obtient une figure similaire à celle-ci :
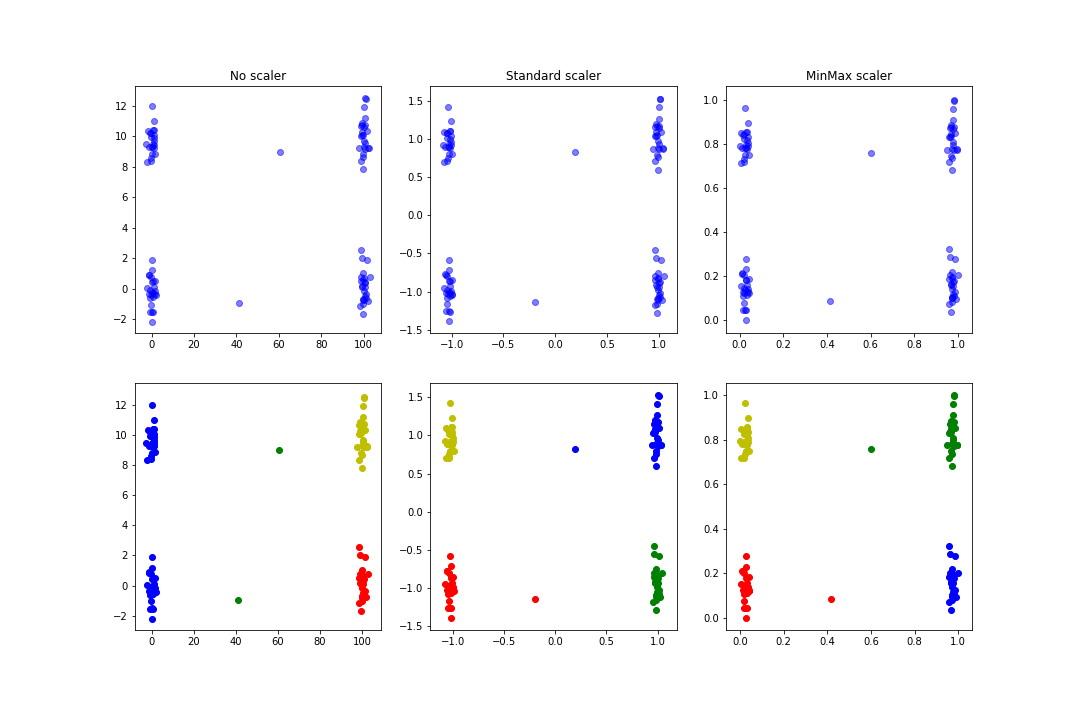
On voit que les clusters trouvés dans le cas de la normalisation sont plus logiques que dans le cas avant normalisatoion.
La principale différence entre la normalisation standard et la normalisation min-max se trouve dans des cas où on retrouve des valeurs extrêmes. La normalisation standard suppose une distribution normale de la variable pour ramener les valeurs entre -1 et 1 pour la majorité. Dans l’exemple suivant, la variable b a quelques valeurs extrêmes. On remarque que la normalisation n’en ramène pas les valeurs sur cet intervalle :
a = np.random.normal(loc=0, scale=2, size=1000)
a[:500] = a[:500]
b = a.copy()
b[:20] = b[:20] + 10
df = pd.DataFrame({'a': a, 'b': b})
df_standard = df.copy(deep=True)
df_minmax = df.copy(deep=True)
df_standard[df_standard.columns] = StandardScaler().fit_transform(df_standard)
df_minmax[df_minmax.columns] = MinMaxScaler().fit_transform(df_minmax)
fig, axes = plt.subplots(nrows=2, ncols=3, figsize=(20, 15))
axes[0, 0].hist(df['a'], bins=100, color='b')
axes[0, 1].hist(df_standard['a'], bins=100, color='r')
axes[0, 2].hist(df_minmax['a'], bins=100, color='g')
axes[0, 0].set_title('No scaler')
axes[0, 1].set_title('Standard scaler')
axes[0, 2].set_title('MinMax scaler')
axes[0, 0].set_ylabel('a')
axes[1, 0].set_ylabel('b')
axes[1, 0].hist(df['b'], bins=100, color='b')
On obtient une figure similaire à celle-ci :
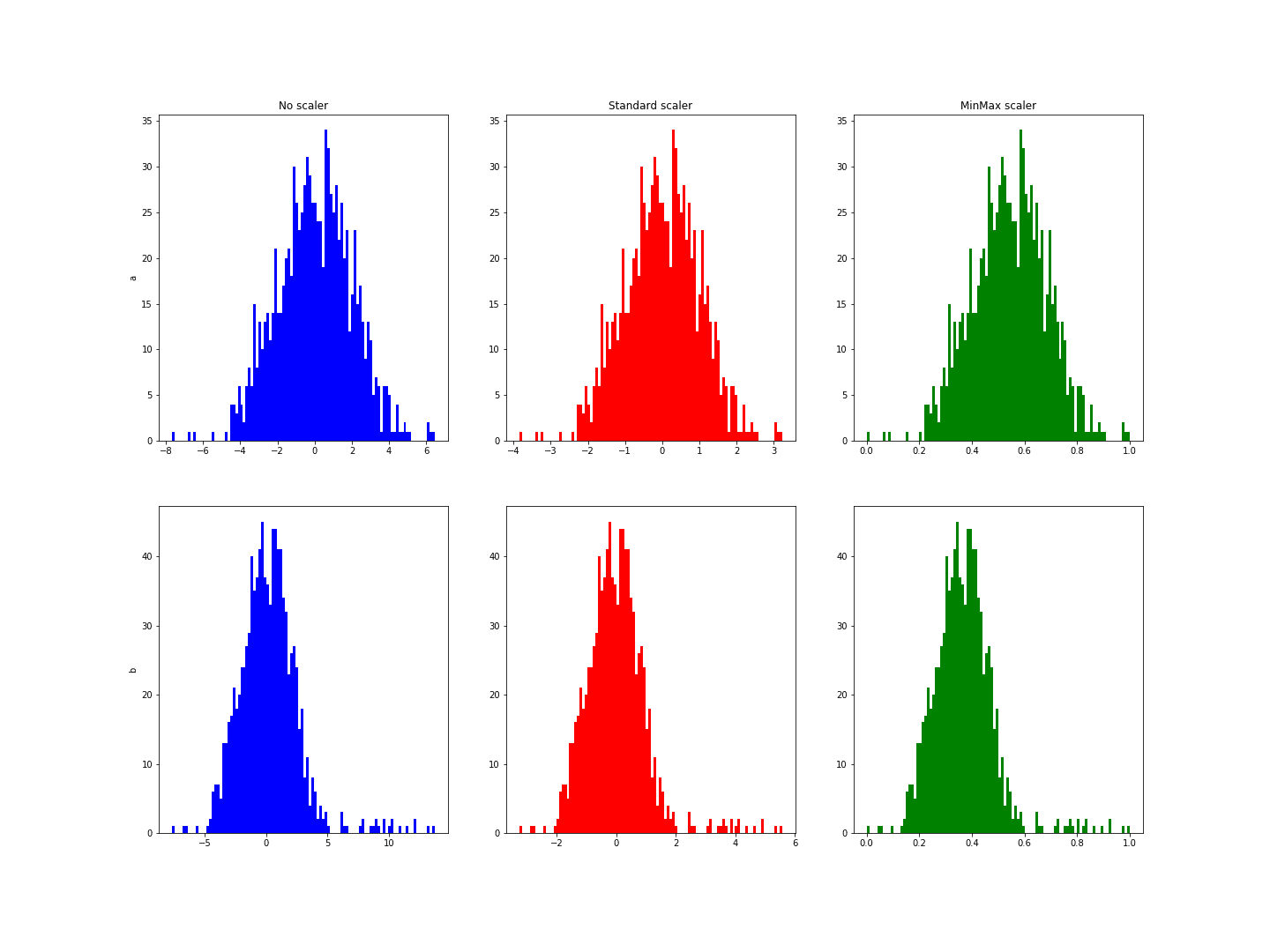
Ces histogrammes montrent un intervalle allant de -3 à 6 pour la variable b alors qu’il allait de -3 à 3 pour a.
Évidemment dans ces deux cas, nous avons volontairement ajouté des valeurs aberrantes pour forcer le trait. Lors d’un projet de Data Science ces valeurs auront été enlevées plus tôt mais ces exemples donnent une idée de ce que la normalisation peut apporter pour les variables quantitatives.
Préparer une variable qualitative
On l’a dit plus tôt mais les algorithmes de Machine Learning ne prennent pas de variables non numériques en entrée (en tout cas pour Python et scikit-learn). Il faut donc transformer ces données. Là encore il faut distinguer plusieurs cas.
- Si il existe une hiérarchie entre les différentes modalités clairement établie, alors on peut sans doute se ramener à une variable quantitative: par exemple, si une de nos variables est une note de A à F, alors on doit pouvoir ramener ces notes à des valeurs comprises entre 0 et 20 avec F < E < D < C < B < A. Si on s’intéresse à des produits disponibles sur un site de e-commerce, neuf pourrait valoir 20, bon état 15, passable 10, endommagé 7, … Auquel cas, il suffit à présent de se reporter au paragraphe précédent.
- Mais dans le cas où il n’y a pas de hiérarchie, quel problème y a-t-il à utiliser ce même genre de signature ? Si par exemple, je considère un jeu de données de modèles de voitures et que nous avons la variable couleur avec trois modalités (disons bleu, rouge et vert): si j’attribue les codes 0, 1 et 2 aux couleurs, alors je me rends compte que bleu < rouge < vert, ce qui est tout-à-fait discutable ! De plus, mathématiquement, cela voudrait dire que bleu + bleu = bleu, ce qui est jusque là assez juste, mais aussi que bleu + rouge = rouge, ce qui commence à être plutôt embêtant et enfin, rouge + rouge = vert ce qui n’est vrai qu’en cas de daltonisme ! Un autre problème soulevé est que la différence entre le bleu et le vert est deux fois plus grande qu’entre le bleu et le vert, ce qui est discutable là encore.
df = pd.DataFrame({'couleur': ['bleu', 'rouge', 'vert']})
# encoder avec 0, 1, 2
code = {'bleu': 0, 'rouge': 1, 'vert': 2}
df_1 = df.copy(deep=True)
df_1['couleur'] = df_1['couleur'].apply(lambda c: code.get(c))
print(df_1.head())
from scipy.spatial import distance_matrix
import seaborn as sns
print('\nMatrices de distance')
plt.figure(figsize=(20, 20))
sns.heatmap(distance_matrix(df_1, df_1), annot=True)
plt.show()
Dans cet exemple, on se rend bien compte que la distance est plus importante entre les observations correspondant aux couleurs bleu et vert qu’entre les observations correspondant aux couleurs bleu et rouge ou rouge et vert.
Il faut donc passer par une binarisation des données: chaque modalité va se transformer en variable indicatrice: au lieu d’avoir une variable, nous en aurons 3 avec chacune des 0 et des 1: dans la colonne rouge, ne vaudront 1 que les observations correspondant aux véhicules de couleur rouge…
df_2 = df.copy(deep=True)
df_2 = pd.get_dummies(df_2)
print(df_2.head())
print('\nMatrices de distance')
plt.figure(figsize=(20, 20))
sns.heatmap(distance_matrix(df_2, df_2), annot=True)
plt.show()
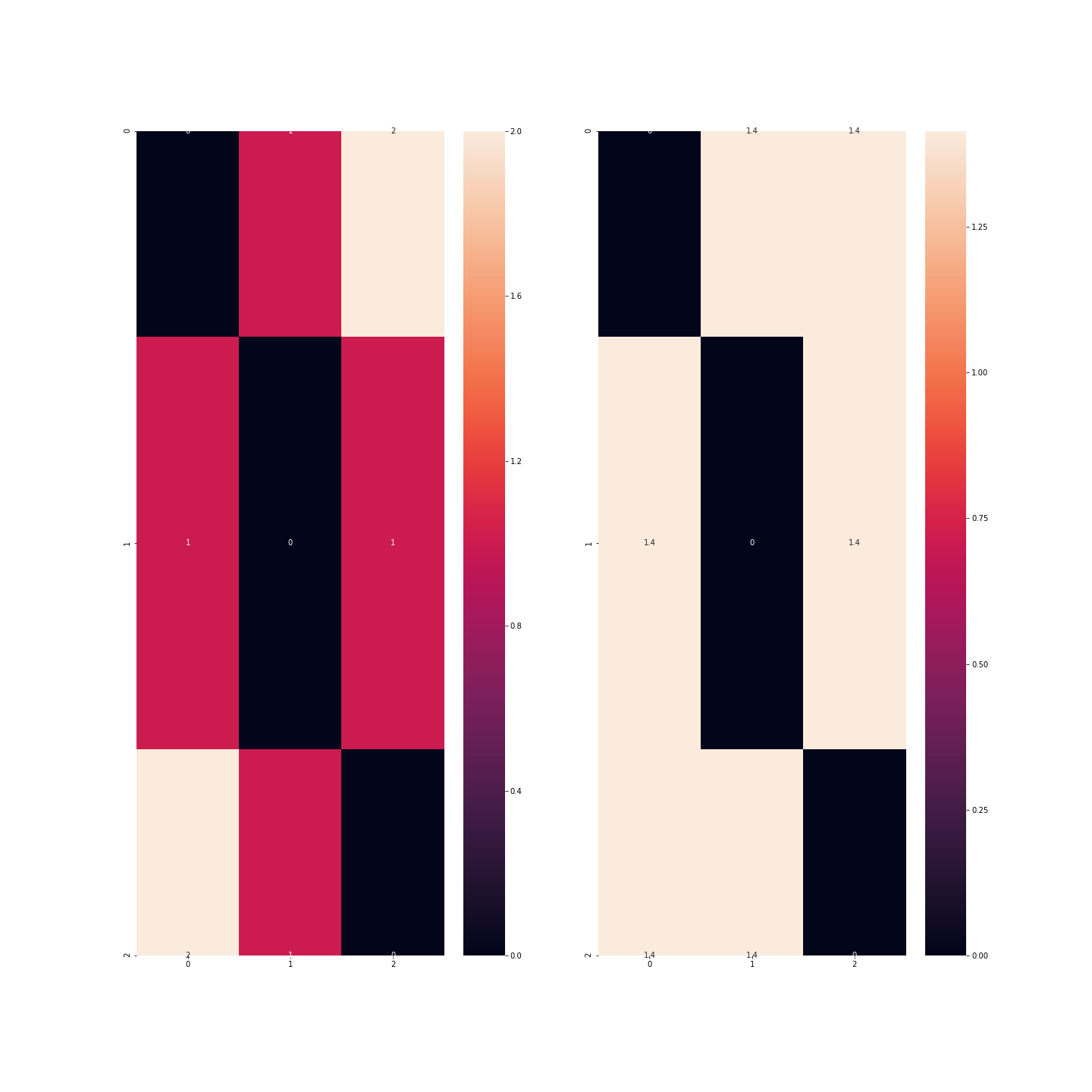
Il y a cependant un point sur lequel nous devons revenir dans cette histoire: si nous prenons autant de colonnes que de modalités, alors l’information contenue dans mon jeu de données est redondante. On peut donc se passer d’une de ces modalités puisqu’elle est sous-entendue par les autres qui seront alors toutes nulles: cette technique permet d’alléger le jeu de données mais surtout d’enlever une variable trop corrélée avec les autres: Si il y a beaucoup de modalités, alors la plupart des indicatrices de ces variables seront nulles pour beaucoup d’observations et elles seront nulles en même temps.
Mais il nous reste une catégorie à évoquer : les variables circulaires.
Préparer une variable circulaire
Une variable circulaire est une variable quantitative, ou qualitative qui boucle sur elle-même: les mois de l’année, l’heure de la journée, les saisons, le stade de vie d’un produit recyclable à l’infini, … Ces variables ont ceci de spécial qu’on peut définir une hiérarchie entre les différentes valeurs, mais que cette hiérarchie est circulaire: 1h du matin serait supérieur à 0h de la même façon que 0h serait supérieur à 23h; De même, printemps < été < automne < hiver < printemps < …
Il faut donc trouver un moyen d’encoder ces données sans pour autant perdre trop de sens. On prendra l’exemple des heures de la journée: pour l’instant ces données sont représentées sous la forme de nombre allant de 0 à 23.
df = pd.DataFrame({'heure': [i for i in range(24)]})
print(df.head())
Si on conserve ce format, on va donc avoir la distance entre 23h et 0h qui va valoir 23 fois la distance entre 0h et 1h. Or nous savons très bien que ce n’est pas le cas: au contraire, le comportement d’un individu à 23h, à minuit ou à 1h du matin est certainement très similaire.
plt.figure(figsize=(20, 20))
sns.heatmap(distance_matrix(df, df), annot=True)
plt.show()
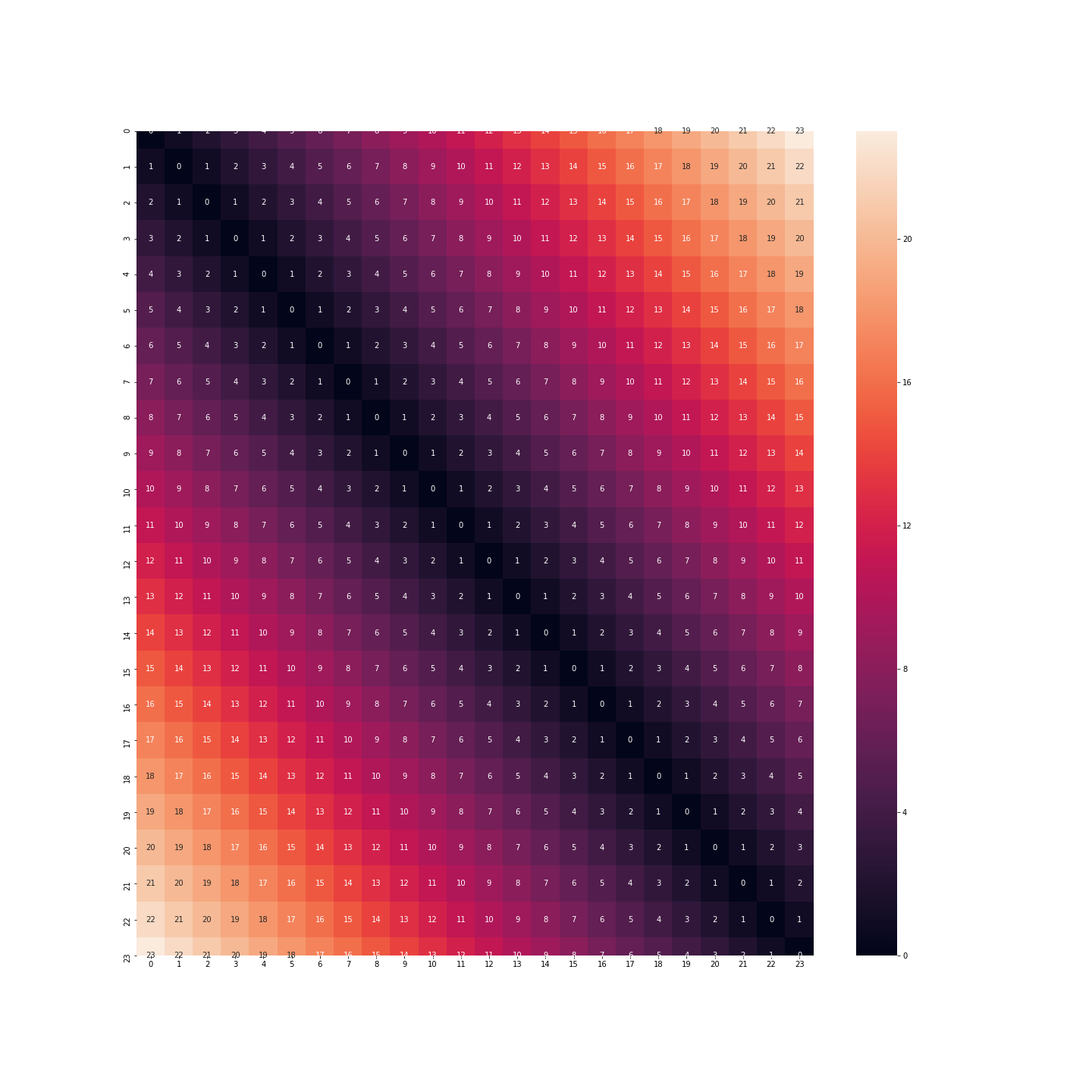
Que dire de la binarisation: cette fois-ci nous n’avons plus le même problème. La distance entre minuit et 1h est la même qu’entre 23h et minuit.
df_2 = df.copy(deep=True)
df_2 = pd.get_dummies(df_2, columns=['heure'])
print(df_2.head())
plt.figure(figsize=(20, 20))
sns.heatmap(distance_matrix(df_2, df_2), annot=True)
plt.show()
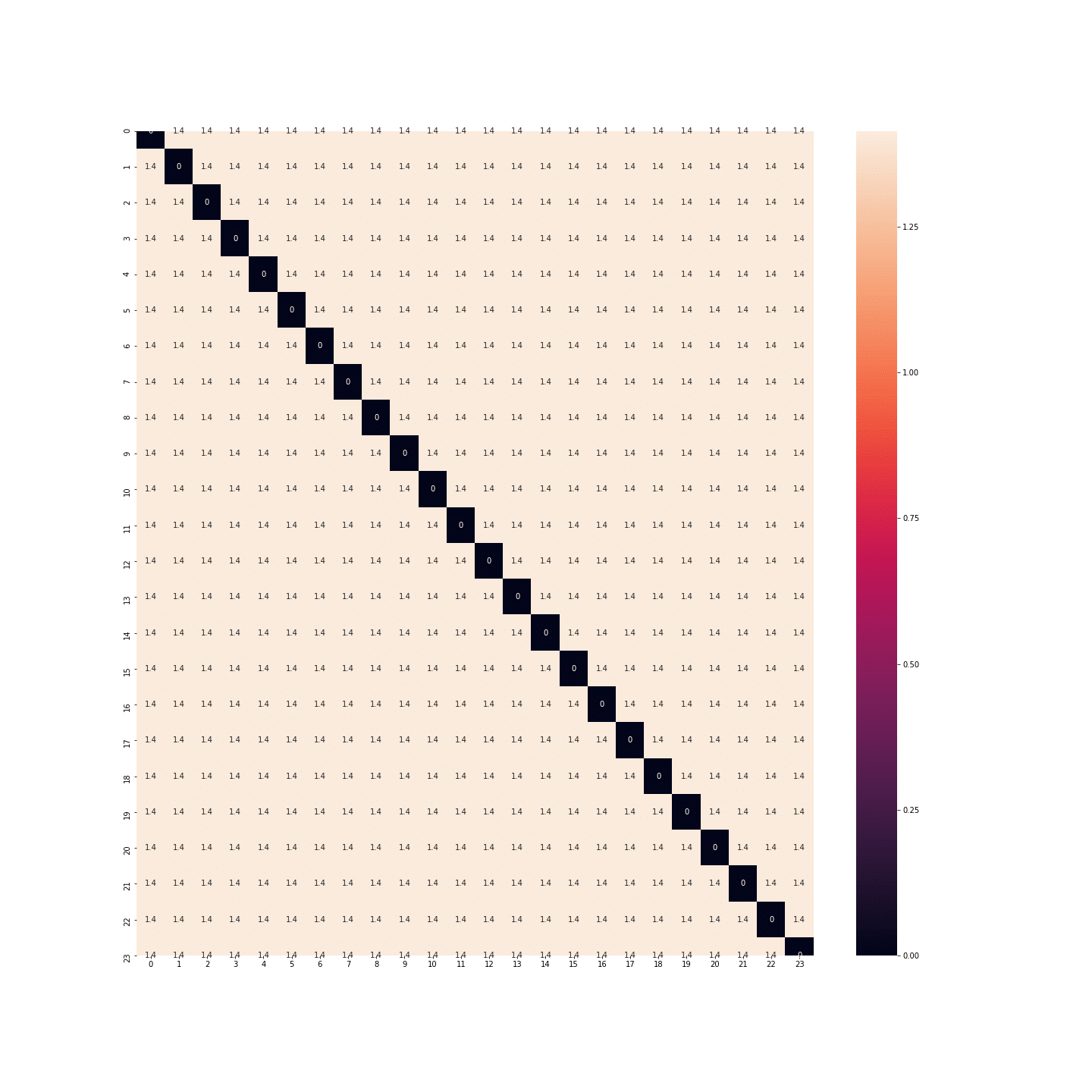
En fait, les distances sont les mêmes entre toutes les heures… Il y autant d’espace entre minuit et 1h qu’entre minuit et midi… Or là encore, ce n’est pas bon.
Il faut donc trouver une autre solution. Cette autre solution vient de la trigonométrie. On ne va pas garder les valeurs absolues, mais prendre simplement le cosinus et le sinus de ces valeurs :
df_3 = df.copy(deep=True)
df_3['sin_heure'] = df_3['heure'].apply(lambda h: np.sin(2 * np.pi * h / 24))
df_3['cos_heure'] = df_3['heure'].apply(lambda h: np.cos(2 * np.pi * h / 24))
df_3.drop(['heure'], axis=1, inplace=True)
plt.figure(figsize=(20, 20))
sns.heatmap(distance_matrix(df_3, df_3), annot=True)
plt.show()
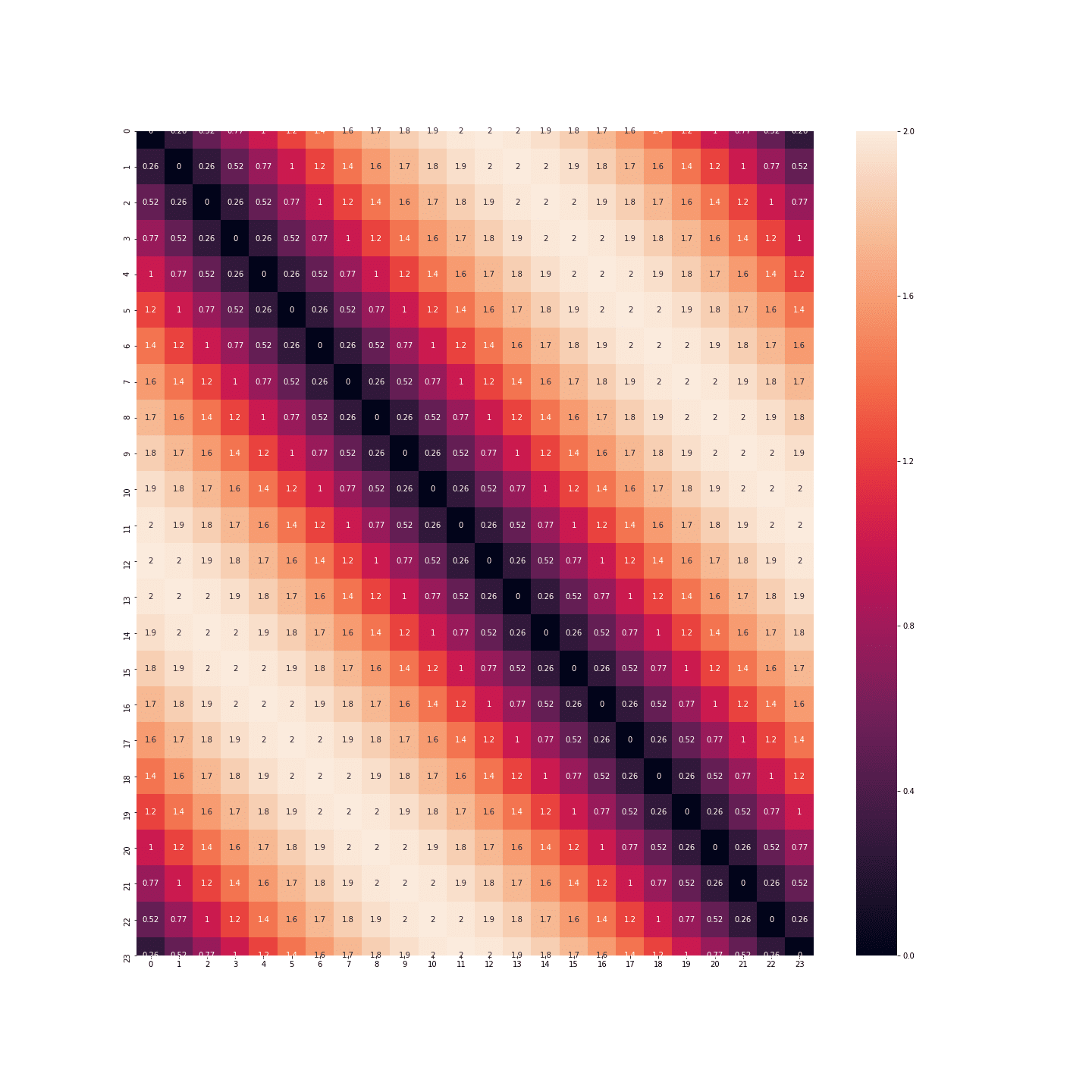
Les distances sont bien plus nuancées ! On peut même représenter les points dans un plan pour voir que nous venons de réinventer l’horloge :
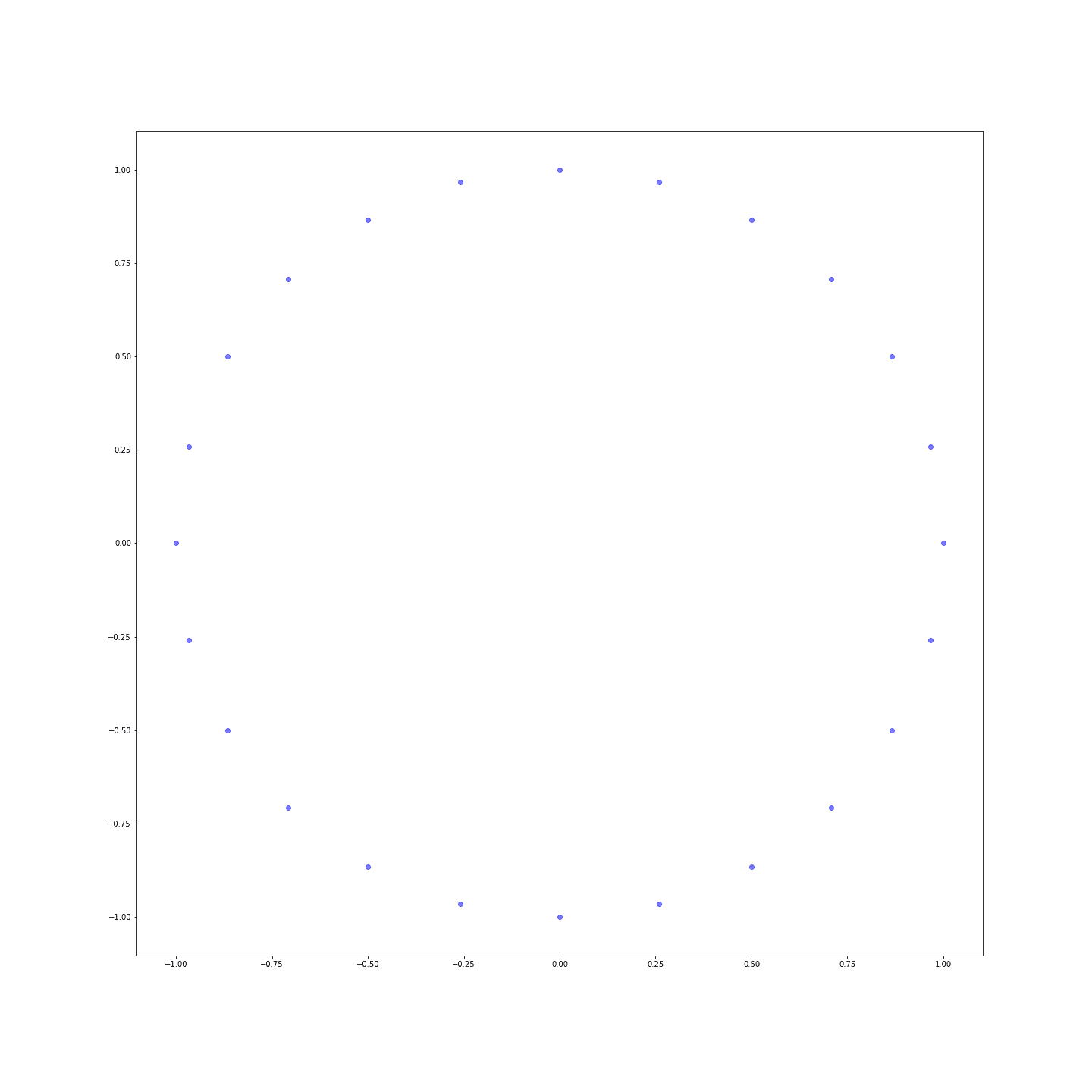
Conclusion
Cette étape de construction de préparation des variables juste avant entraînement d’un algorithme de Machine Learning est cruciale car elle permet à la fois d’accélérer les algorithmes et d’améliorer les résultats. Les techniques sont différentes pour les différents types de variable mais il faut les garder à l’esprit pour bien partir avant l’application d’algorithmes.
Vous souhaitez en apprendre davantage ? Rejoignez l’une de nos prochaines formations en format Bootcamp ou continu.
Contactez-nous à contact@datascientest.com ou sur Linkedin sur la page DataScientest !










