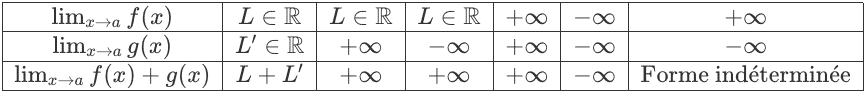Toutes les disciplines scientifiques se basent sur les mathématiques et la data science n’y fait pas exception. Lorsque les problèmes à résoudre sont des problèmes d’optimisation, il est nécessaire de maîtriser ce qu’est la limite d’une fonction. Dans cet article, vous découvrirez comment déterminer la limite d’une fonction.
Limite : Définition
La limite d’une fonction f correspond à la valeur vers laquelle se rapproche la fonction lorsque son argument se rapproche d’une certaine valeur.
Mathématiquement, on écrit
\lim \limits_{x \to a} f(x) = l
On dit que f tend vers l lorsque x tend vers a.
Selon les cas, a et l peuvent être des nombres réels, ou bien être égaux à \pm \infty.
Limites des fonctions usuelles
- Limites finies en une valeur réelle
Par exemple, pour f(x) = x^2, la limite quand x tend vers 2 est 2^2 = 4.
- Limites à l’infini
Lorsque la fonction est bien définie en un nombre réel a (on dit qu’elle est continue en a), alors la limite en a vaut exactement f(a).
Lorsque la variable x prend des valeurs très grandes (positivement ou négativement), on dit que x tend vers plus ou moins l’infini. Dans ce cas, on distingue les cas où f(x) se rapproche d’une valeur finie et ceux où f(x) s’éloigne vers l’infini. Dans ce premier cas, on dit que f converge, et dans le second que f diverge.
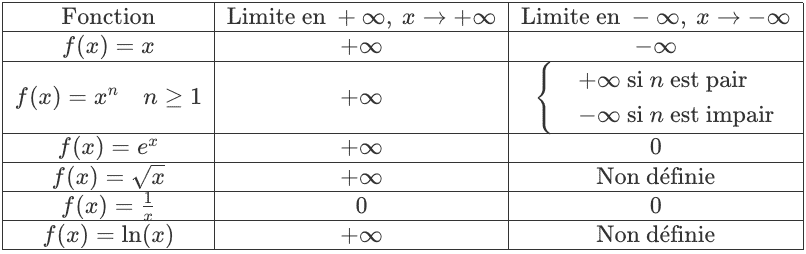
Ci-dessous, un tableau résumant les limites de fonctions usuelles à l’infini
\begin{array}{|c|c|c|}
\hline \text{Fonction} & \text{Limite en }+ \infty, \: x \to +\infty & \text{Limite en }-\infty ,\:x \to - \infty \\
\hline f(x) = x & +\infty & -\infty \\
\hline f(x) = x^n \quad n \geq 1 & +\infty & \begin{cases} & + \infty \text{ si } n \text{ est pair } \\ & - \infty \text{ si } n \text{ est impair} \end{cases} \\
\hline f(x) = e^x & +\infty & 0 \\
\hline f(x) = \sqrt{x} & +\infty & \text{Non définie} \\
\hline f(x) = \frac{1}{x} & 0 & 0 \\
\hline f(x) = \ln(x) & +\infty & \text{Non définie} \\
\hline
\end{array}
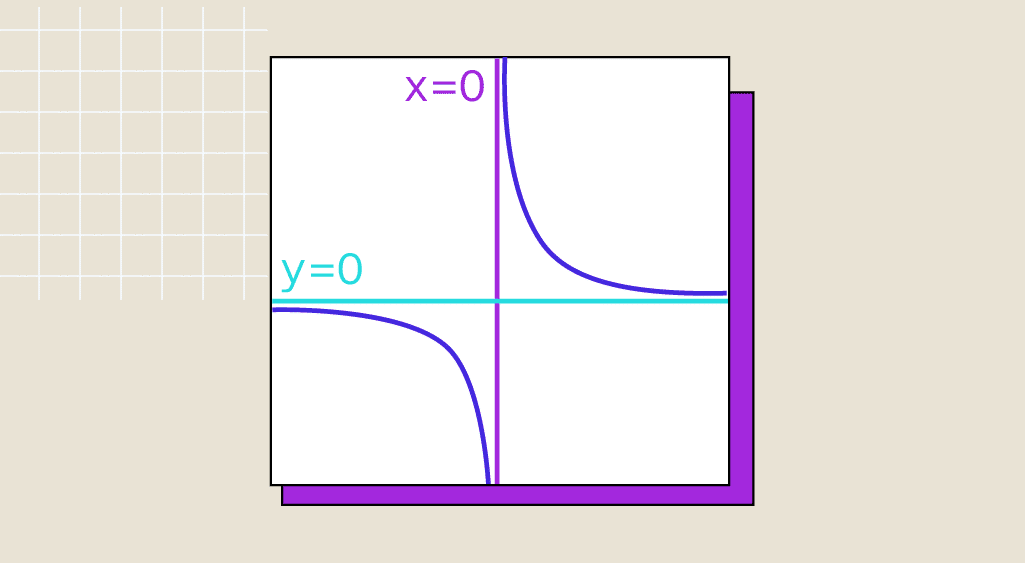
Lorsqu’une fonction admet une limite finie l \in \mathbb{R} quand x \to \infty, alors on dit que f admet une asymptote horizontale d’équation y = l. C'est-à-dire que la courbe se rapproche de plus en plus de la droite y=l.
- Limites infinies en une valeur finie
\begin{array}{|c|c|}
\hline \text{Fonction} & \text{Limite en } 0, \: x \to 0 \\
\hline f(x) = \frac{1}{x} & \begin{cases} & +\infty \text{ si } x \gt 0 \\ & \infty \text{ si } x \lt 0 \end{cases} \\
\hline nan & nan \\
\hline f(x) = \ln(x) & -\infty \\
\hline f(x) = \sqrt{x} & 0 \\
\hline
\end{array}
Lorsque \lim_{x \to a} f(x) = \pm \infty, avec a un réel, alors on dit que la courbe de f admet une asymptote verticale en a. C’est-à-dire que la courbe se rapproche de plus en plus de la droite d’équation x=a.
Opérations sur les limites
Dans la majorité des cas, il est possible de faire des opérations sur les limites pour déterminer la limite.
Limite d’une somme de deux fonctions
Limite d’un produit de deux fonctions
Limite d’un quotient de deux fonctions
Cliquez sur les tableaux pour les afficher en plein écran.
Déterminer une limite en pratique
Pour déterminer des limites, il est parfois plus simple d’utiliser d’autres fonctions.
Comparer les fonctions permet de comparer leurs limites, lorsqu’elles existent.
Comparer les fonctions permet de comparer leurs limites, lorsqu’elles existent.
Il existe deux grandes propriétés de comparaison des fonctions
- Théorème de comparaison
Soient f et g deux fonctions définies sur un intervalle I = [a, +\infty[ .
On suppose que pour tout x \in I \; f(x) \geq g(x).
On suppose que pour tout x \in I \; f(x) \geq g(x).
Si \lim_{x \to +\infty}g(x) = +\infty, alors \lim_{x \to +\infty}f(x) = +\infty
Si \lim_{x \to +\infty}f(x) = -\infty, alors \lim_{x \to +\infty}g(x) = -\infty
- Théorème des gendarmes
Soient f, g et h trois fonctions définies sur un intervalle I = [a, +\infty[.
On suppose que pour tout x \in I \; g(x) \leq f(x) \leq h(x).
On suppose que pour tout x \in I \; g(x) \leq f(x) \leq h(x).
Si g et h tendent vers la même limite l en +\infty, alors \lim_{x \to +\infty}g(x) = +\infty
Vous savez désormais ce qu’est une limite et comment la calculer. Le calcul des limites permet par exemple de définir la dérivée d’une fonction comme la limite d’un taux d’accroissement.
Pour en savoir plus, vous pouvez consulter notre article sur la dérivation d’une fonction.
Si vous souhaitez découvrir tous les concepts mathématiques impliqués en data science, nous vous invitons à découvrir nos cursus.
Si vous souhaitez découvrir tous les concepts mathématiques impliqués en data science, nous vous invitons à découvrir nos cursus.