Le nombre d’expected goals est un nouvel indicateur de performances apparu très récemment dans l’analyse du football. Cette statistique est de plus en plus utilisée pour interpréter la physionomie d’une rencontre, mais savons nous vraiment comment l’interpréter ?
Cet article a pour but de vous présenter le plus simplement possible les réalités mathématiques qui se cachent derrière les expected goals (xG). Les résultats présentés sont issus d’une simulation réalisée par David Sumpter sur la chaîne youtube Friends of Tracking sur les données de la première league sur une saison entière .
Qu’est-ce qu’un expected goal ?
Qu’est-ce qu’un xG ? A quoi correspond un score de 2.71 à 0.78 en xG ?
A chaque tir effectué lors d’un match, il est possible d’attribuer une probabilité pour que la balle se retrouve au fond des filets
Par exemple, un tir des 35 mètres aura une très faible probabilité de réussite (peut-être 5% donc 0.05 xG) alors qu’un tir sur pénalty aura de bonnes chances de tromper le gardien (76% donc 0.76 xG). En additionnant les expected goals de tous les tirs d’un match, nous obtenons donc un score en xG.
Par rapport au score classique qui ne comptabilise que les buts, l’avantage des xG est qu’ils sont calculés sur un plus grand nombre d’événements. Ils reflètent donc souvent la physionomie d’une rencontre et permettent bien souvent d’identifier l’équipe qui a eu les plus grosses occasions.
Mais alors comment est calculée cette probabilité ?
Pour comprendre cela, construisons ensemble un modèle d’expected goals très simple. Partons de l’intuition suivante : plus vous êtes loin du but, plus vous aurez de mal à marquer. Dans notre modèle, la probabilité de marquer sera établie en ne considérant que la position du tir.
Nous allons donc visualiser la répartition des tirs dans l’espace en 2 dimensions.
Voici ce que l’on obtient sur une saison complète de football en première league :
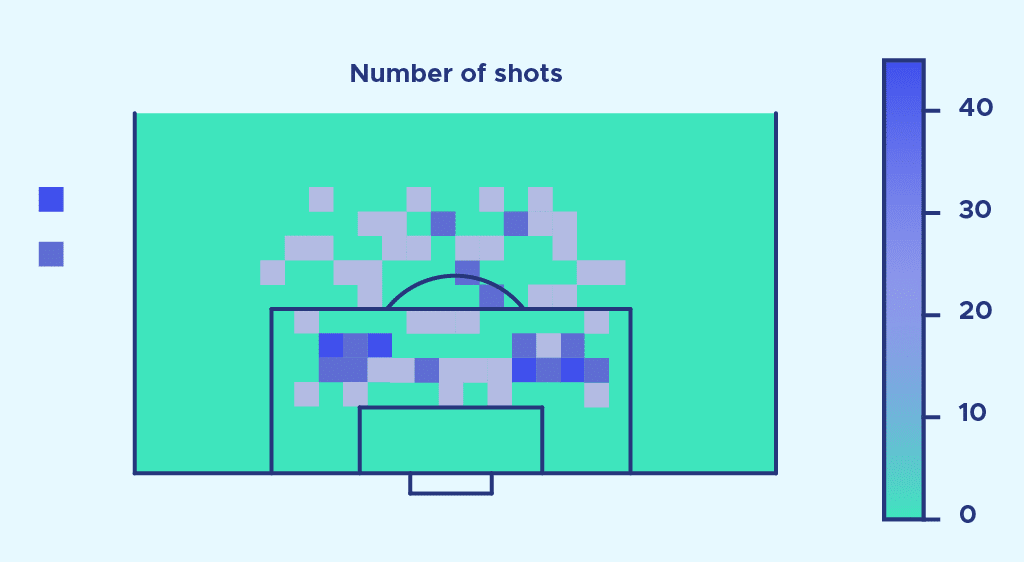
Maintenant comparons à la répartition du nombre de buts marqués :
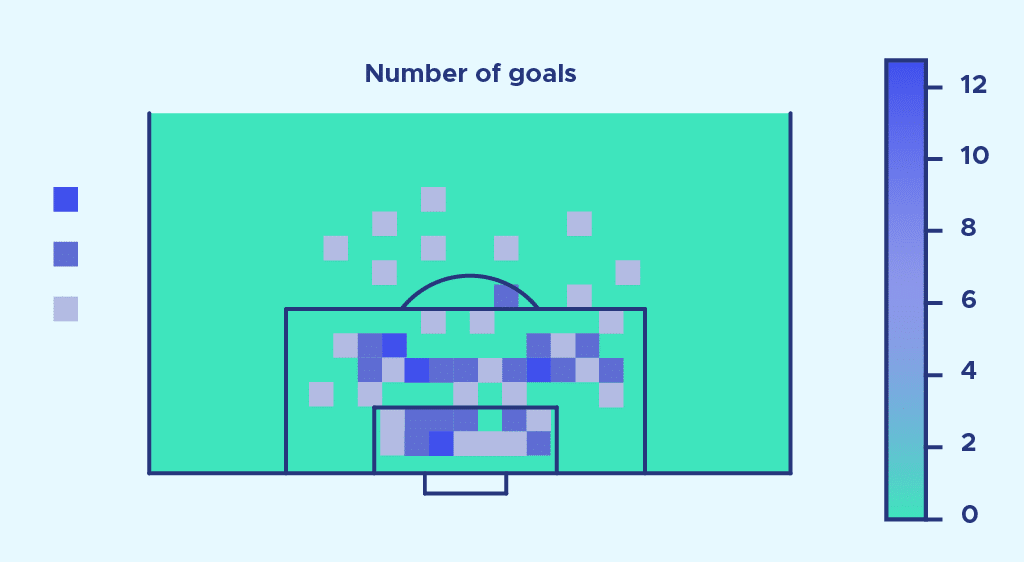
On remarque que le nombre de tirs en dehors de la surface semble être proportionnellement bien plus important que le nombre de buts.
Maintenant rappelons nous que notre objectif est d’établir une probabilité de but pour chaque tir. Pour cela, nous effectuons le rapport nombre de buts/nombre de tirs nombre de buts nombre de tirs pour chaque zone quadrillée de l’espace. Ce rapport est notre probabilité de marquer. Ensuite nous affichons cette probabilité pour chaque zone de l’espace et voilà le résultat :
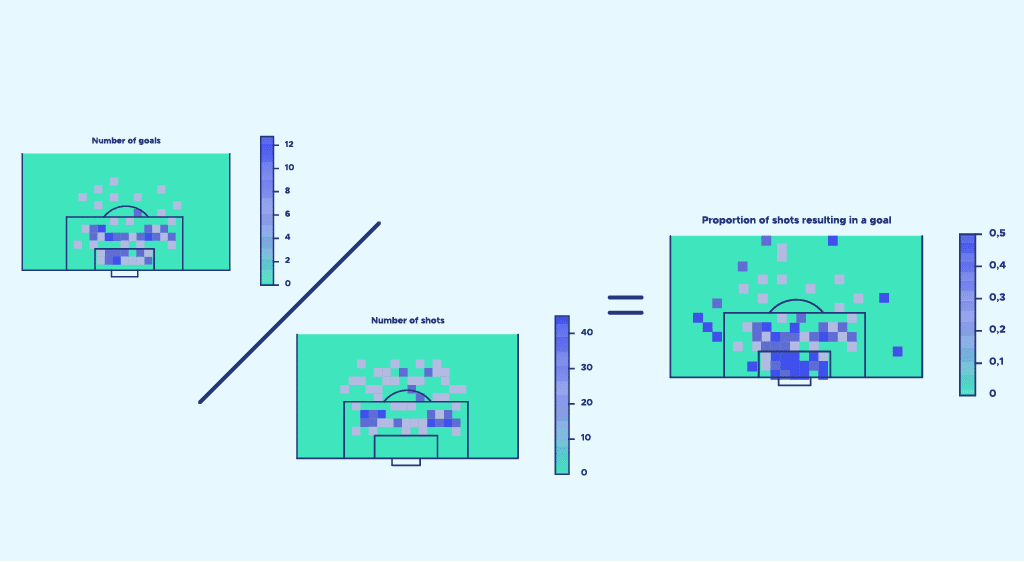
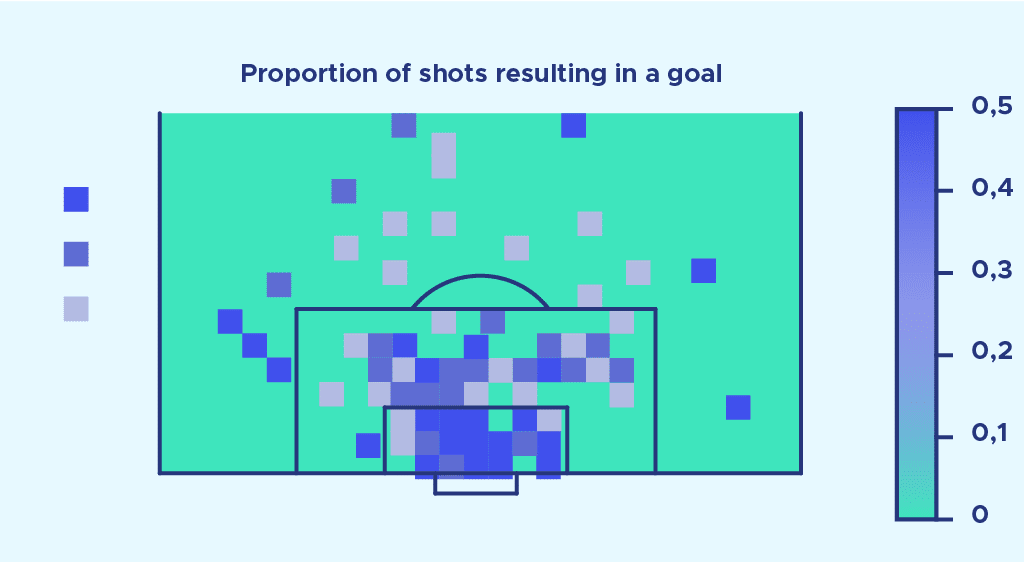
Cette image est un premier modèle d’expected goals. Mais comme vous pouvez vous en rendre compte, il est loin d’être parfait et possède beaucoup de limites.
La première observation que nous pouvons faire est que le résultat obtenu semble présenter des anomalies.
En effet, certaines zones de l’espace très éloignées semblent avoir une probabilité de marquer très importante.
Ceci est dû au fait que l’exemple considéré ne prend en compte les tirs sur une seule saison, dans un seul championnat. Parfois, il n’y a eu qu’un tir dans une zone très éloignée, et ce tir a été marqué et c’est ce que nous appelons la magie du football. Cependant, si nous avions effectué nos calculs avec beaucoup plus de données (plusieurs championnats sur plusieurs saisons), le résultat obtenu aurait présenté des anomalies moins fortes.
A partir de cette visualisation générée, nous allons maintenant essayer de construire un modèle mathématique qui colle le mieux à la fréquence de buts observée. Pour cela, nous allons étudier deux paramètres séparément : l’angle de tir et la distance au but.
L’angle de tir représente l’angle entre les deux poteaux à l’endroit du tir.
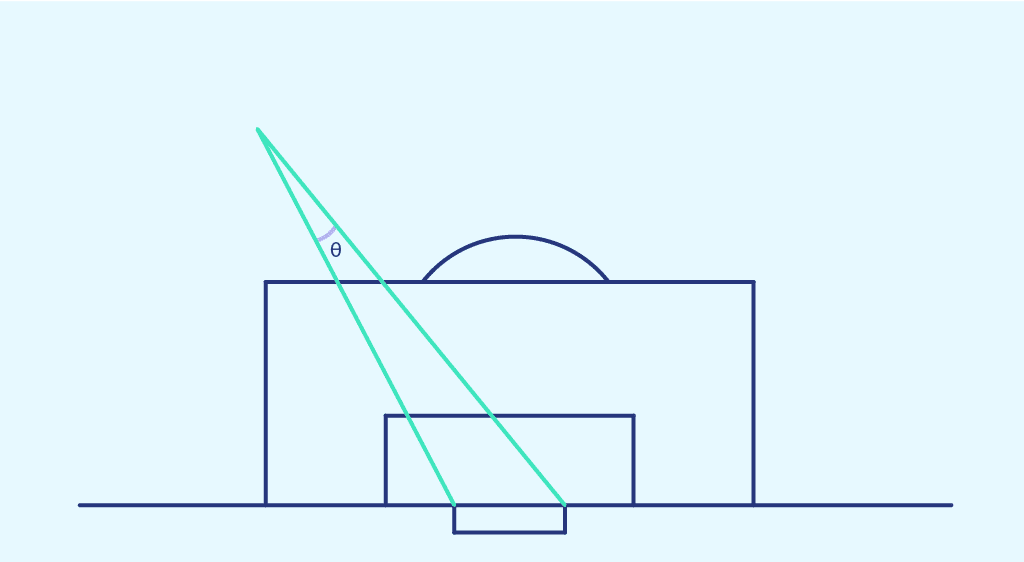
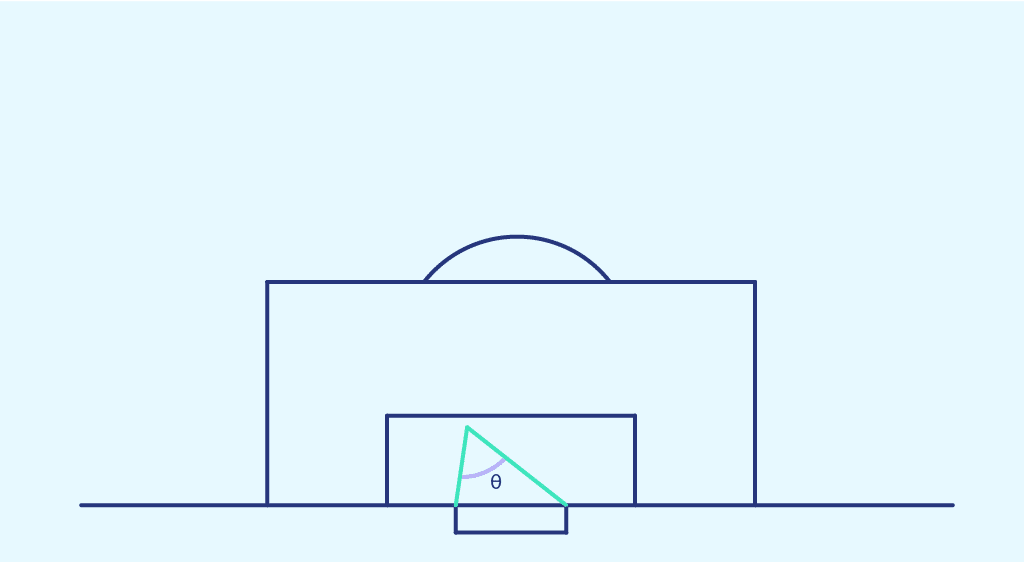
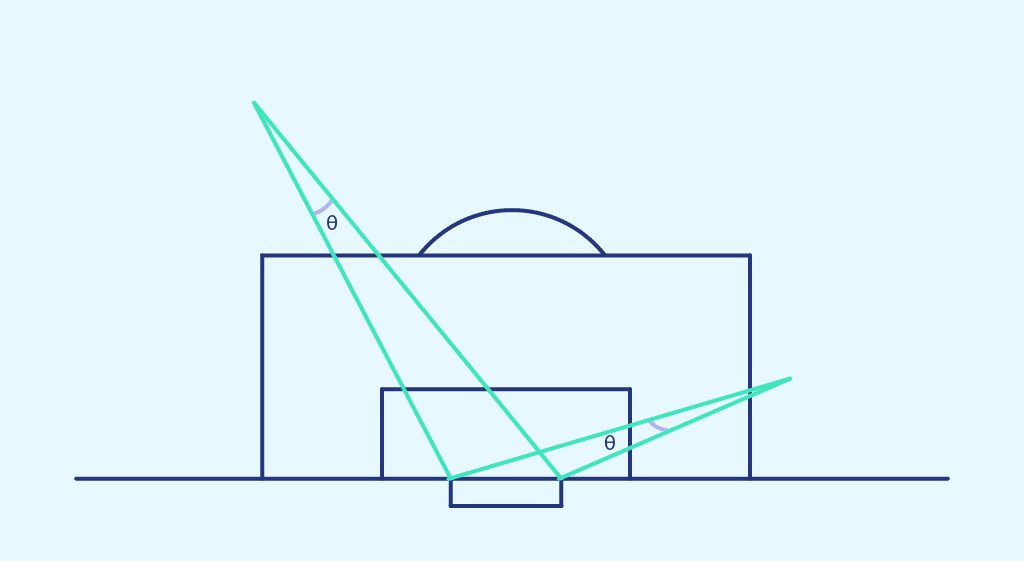
Cette fois-ci, nous représentons la probabilité de marquer obtenue précédemment dans chaque zone de l’espace, en fonction de l’angle de tir de cette zone. On on obtient le nuage de point suivant :
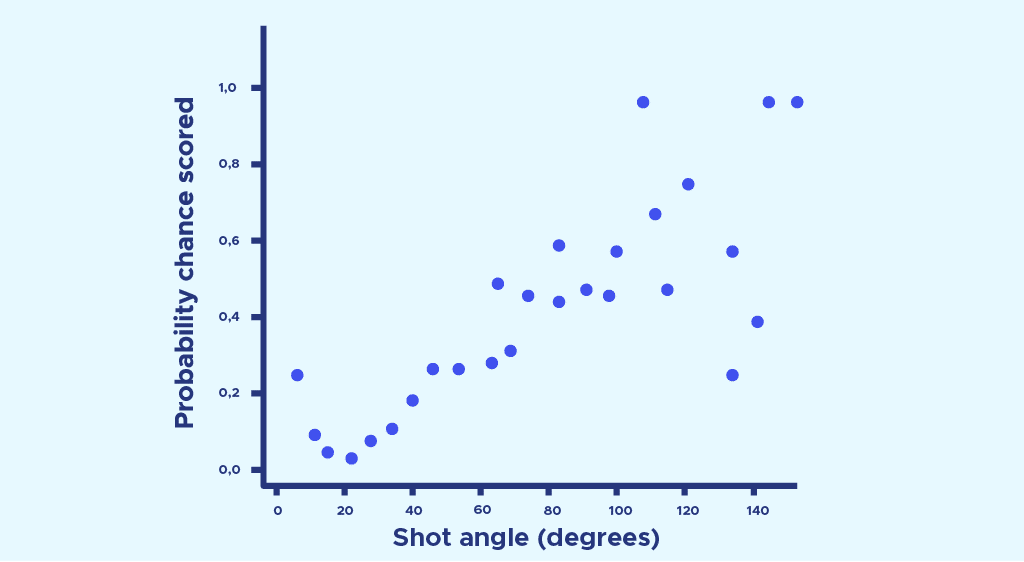
Ensuite, une régression logistique permet d’approcher ces points par la formule : P(theta) = . Nous avons choisi une régression logistique et non une régression linéaire, car elle permet d’avoir une probabilité de marquer qui vaut 1 lorsque l’angle s’approche de 180° et 0 lorsque l’angle vaut 0°. (Pour un petit rappel sur la regression logistique, relisez cet article )
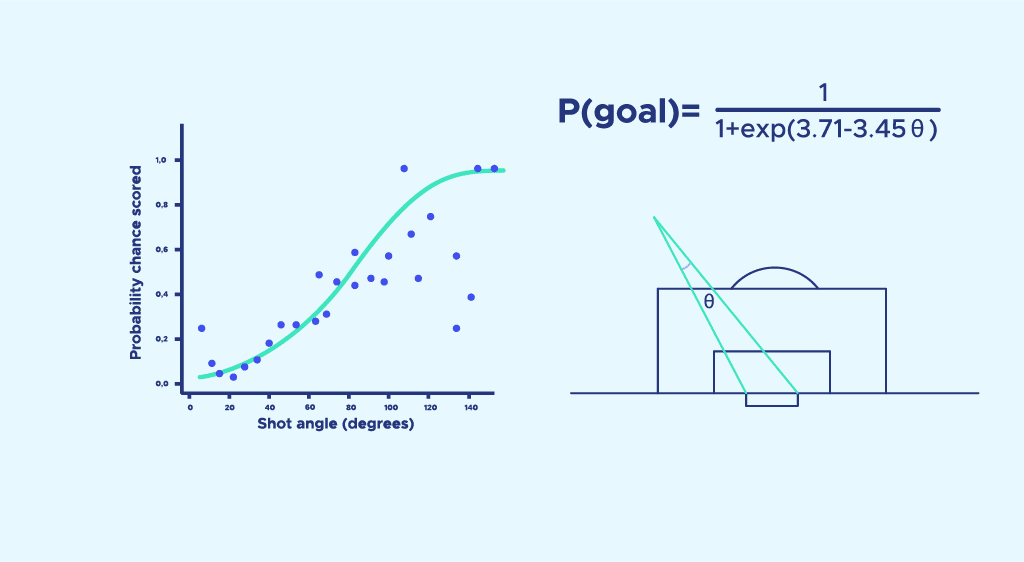
Maintenant, nous pouvons faire exactement la même chose avec la distance :
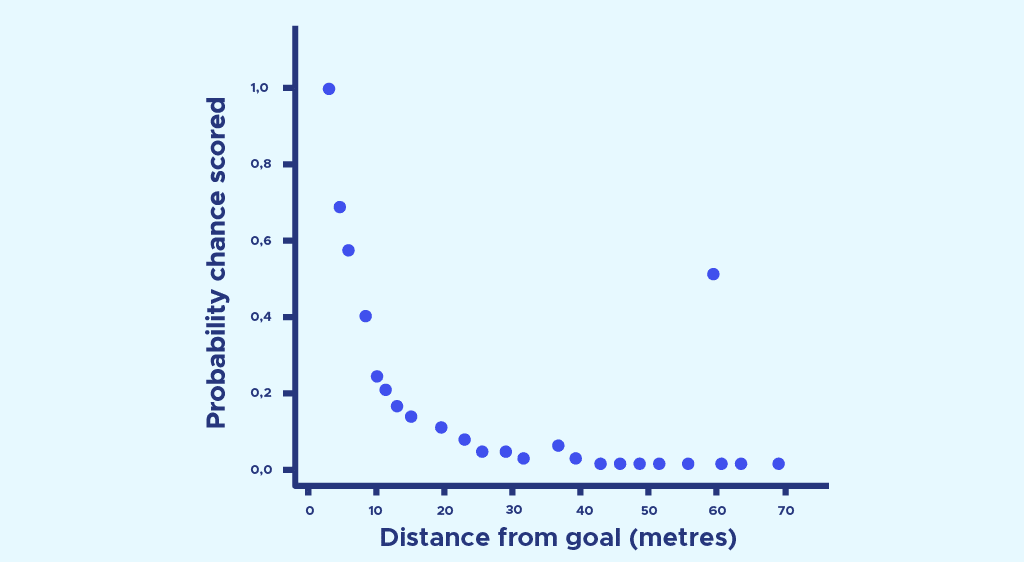
Encore une fois nous faisons une régression logistique, et nous obtenons une probabilité de marquer en fonction de la distance :
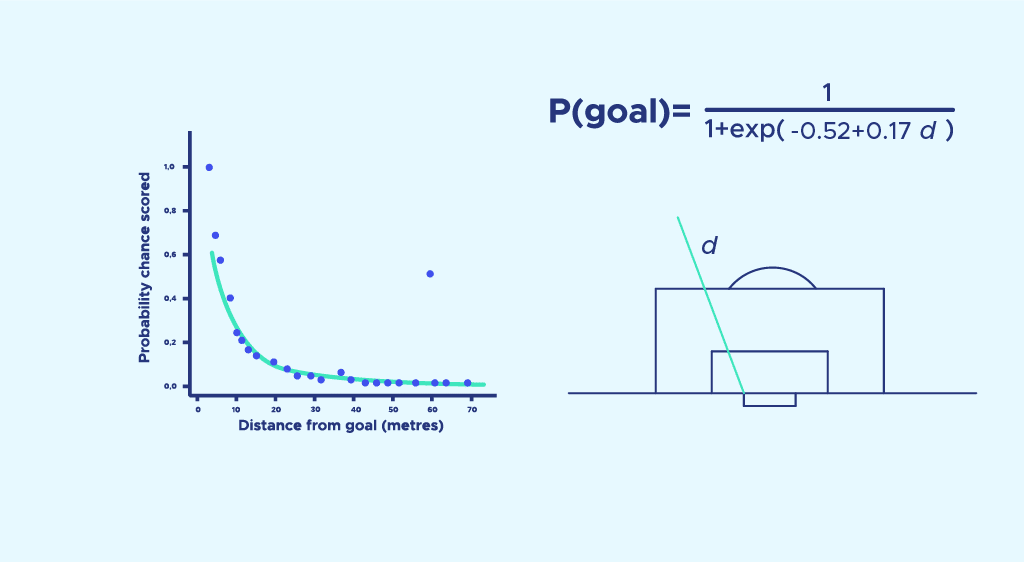
Le modèle n’est pas idéal car la probabilité de marquer à 0 mètre devrait être égale à 1. Il mériterait d’être amélioré (par exemple en ajoutant un d2dans l’exponentielle) mais partons avec cette première approximation.
Ces 2 modèles mathématiques, l’un basé sur l’angle et l’autre sur la distance, prédisent notre probabilité de marquer expérimentale de manière plutôt correcte. Néanmoins ils ne le font pas de manière ultra précise.
Pour améliorer l’exactitude de notre modèle mathématique, nous prenons cette fois ci en compte l’impact de ces 2 dimensions simultanément.
Nous faisons cela à l’aide d’une régression à plusieurs variables mais cela dépasse un peu le cadre théorique de cet article. Le résultat qui émerge de cette régression à deux variables est le suivant :
Le modèle n’est pas idéal car la probabilité de marquer à 0 mètre devrait être égale à 1. Il mériterait d’être amélioré (par exemple en ajoutant un d2dans l’exponentielle) mais partons avec cette première approximation.
Ces 2 modèles mathématiques, l’un basé sur l’angle et l’autre sur la distance, prédisent notre probabilité de marquer expérimentale de manière plutôt correcte. Néanmoins ils ne le font pas de manière ultra précise.
Pour améliorer l’exactitude de notre modèle mathématique, nous prenons cette fois ci en compte l’impact de ces 2 dimensions simultanément.
Nous faisons cela à l’aide d’une régression à plusieurs variables mais cela dépasse un peu le cadre théorique de cet article. Le résultat qui émerge de cette régression à deux variables est le suivant :
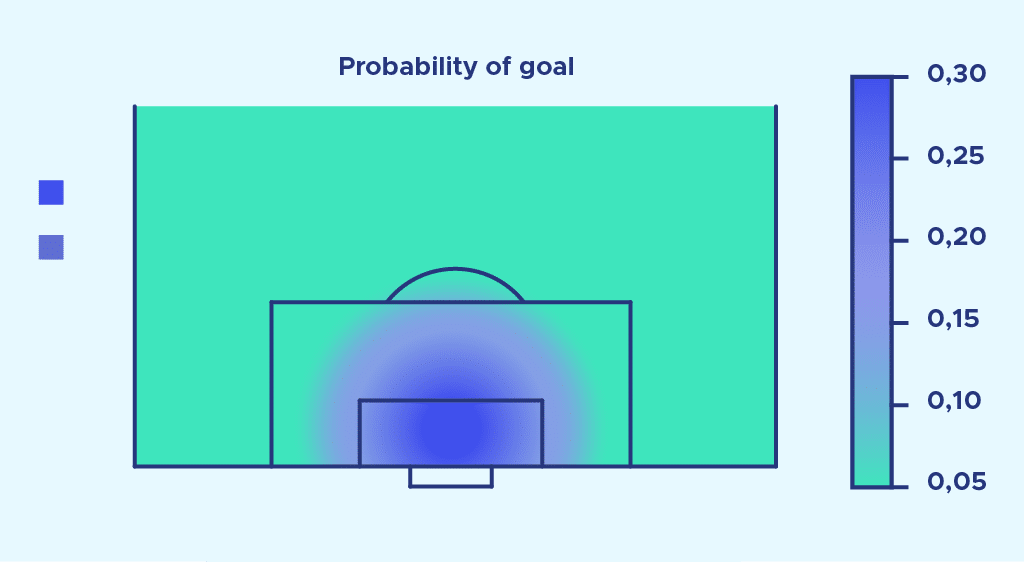
Ce modèle mathématique prend en compte à la fois l’angle et la distance au but du tir effectué. Il est élaboré de manière à coller au mieux à la réalité des buts observés. Il est donc maintenant beaucoup plus général, présente moins d’anomalies et semble mieux se rapprocher de la réalité. A partir de ce modèle, il est ainsi possible d’attribuer une probabilité de marquer aux prochains tirs effectués suivant la zone du tir.
Conclusion
Vous avez vu comment construire, à partir de l’angle et de la distance, un modèle d’expected goals. Ce modèle permet de tirer des premiers enseignements pour les joueurs. Par exemple, on se rend compte qu’il est difficile de marquer lorsque le tir est excentré, et qu’une passe en retrait sera peut-être plus appropriée.
Par ailleurs, notre modèle est loin d’être parfait. Son premier défaut est qu’il est établi sur la base des données d’un seul championnat lors d’une seule saison. Son deuxième défaut est que nous avons pris en compte seulement l’angle et la distance pour l’élaborer. Des modèles plus élaborés prendrons en compte la zone de contact du tir (tête ou pied), la position des défenseurs au moment de la frappe, le type d’action (attaque placée, contre attaque), le choix du pied (bon ou mauvais) et bien d’autres paramètres encore.
S’il y a bien une chose à retenir de cet article, c’est que les expected goals sont construits pour coller au mieux à la fréquence de buts observés en fonction d’une multitude de paramètres. Une probabilité de scorer reste une probabilité. Elle se vérifiera en moyenne sur le long terme si elle est construite correctement, mais sur un seul match tout reste possible et c’est bien cela qui fait la magie de ce sport.
Si vous êtes intéressé par l’analyse de données en rapport avec le football, nous vous recommandons d’aller visiter le projet “MPG, le foot dans toute sa data” développé au sein du studio de DataScientest.








