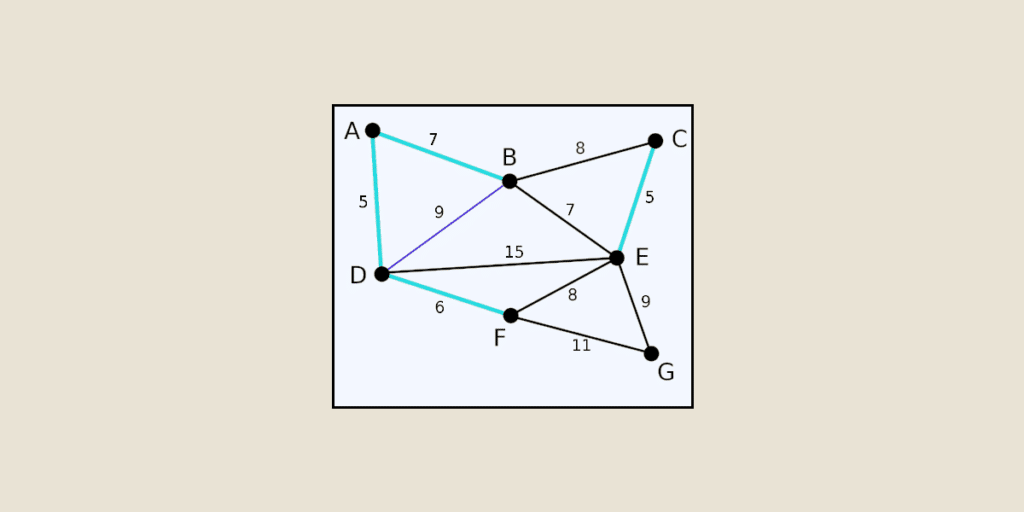
Permettant d’optimiser les connexions au sein d’un réseau, l’algorithme de Kruskal figure parmi les concepts incontournables en Machine Learning. Découvrez son fonctionnement et son intérêt au quotidien.
C’est quoi l’algorithme de Kruskal ?
Conçu en 1956 par Joseph Kruskal, l’algorithme de Kruskal permet de trouver un arbre recouvrant de poids minimum (ARPM) (également appelé arbre couvrant minimum (ACM) ou arbre sous-tendant minimum) dans un graphe connexe non-orienté et pondéré.
Avant de rentrer dans les détails, il convient de définir les termes ci-dessous :
- Arbre : il correspond à un graphique connexe et sans cycle (ou acyclique).
- Graphe connexe : cela signifie qu’il existe un chemin permettant d’accéder à tous les sommets du graphique depuis n’importe quel autre sommet.
- Graphe acyclique : cela signifie que le cycle s’interrompt pour accéder à tous les sommets.
- Graphe pondéré : chaque arête possède un poids.
- Graphe non orienté : chaque arête peut être parcourue dans les deux sens.
- Arbre couvrant : il renvoie à un ensemble d’arêtes d’un graphe pondéré qui contient tous les sommets (mais pas forcément toutes les arêtes). Le poids de l’arbre couvrant est la somme des poids de ses arêtes.
- Arbre recouvrant de poids minimum (ARPM) : il s’agit d’un arbre couvrant dont le poids est le plus petit possible. Autrement dit, il s’agit d’un sous-ensemble d’arêtes qui connecte tous les nœuds du graphe où la somme des poids des arêtes est la plus basse possible.
L’objectif de l’algorithme de Kruskal est justement de retrouver cet arbre recouvrant de poids minimum.
Bon à savoir : en plus de l’algorithme de Kruskal, il est aussi possible d’utiliser l’algorithme de Prim pour trouver un ARPM.
Comment fonctionne l'algorithme de Kruskal ?
Les étapes de l’algorithme de Kruskal
Pour trouver l’arbre recouvrant de poids minimum, l’algorithme de Kruskal prévoit les étapes ci-dessous :
- Trier les arêtes (a) du graphique (G) par poids croissant. Ce faisant, les arêtes les plus légères sont examinées en premières.
- Partir d’un arbre (T) vide. C’est-à-dire un arbre qui ne contient aucune arête ; son poids est égal à 0. Sa construction est progressive en suivant les étapes suivantes.
- Sélectionner les arêtes par poids croissant. Il faut donc commencer par les arêtes les plus légères. Si l’ajout d’une arête n’implique pas la création d’un cycle dans le graphe, il convient de l’ajouter à l’arbre.
- Répétez l’opération jusqu’à ce que tous les sommets (S) soient reliés. Et ce, sans créer de cycle dans l’ARPM.

La traduction mathématique
En mathématique, l’algorithme de Kruskal se traduit comme suit :
- T = ø
- Trier les a de G par valeurs croissantes
- F = { ao }
- Répétez F = { ao } tant que tous les S n’ont pas été intégrés à T
Où
- ao : la plus petite arête non examinée
- T : arbre recouvrant de poids minimum
- G : graphique
- S : sommet
- p : le nombre d’arêtes déjà placées dans le graphe G
- n : le nombre de sommets du graphe G
- F = { ao } :ajout de la plus petite arête non examinée
Bon à savoir : Le nombre d’arêtes d’un ARPM peut varier de (n-1)n/2 .Moins l’arbre recouvrant de poids minimum contient d’arêtes, plus l’algorithme de Kruskal est rapide.
Pourquoi utiliser l’algorithme de Kruskal ?
Dans la pratique, cet algorithme est souvent utilisé pour résoudre des problèmes pratiques tels que la conception de réseaux de communication à moindre coût, la planification de câblage, la suppression des liaisons maritimes les moins rentables tout en préservant l’accessibilité aux différents ports, etc.
Quelle que soit l’utilisation concrète, l’algorithme de Kruskal permet d’optimiser les connexions. C’est justement pour cette raison qu’il est particulièrement utile en Machine Learning. En optimisant le poids des connexions, il permet d’optimiser l’efficacité des modèles d’apprentissage automatique.
Bon à savoir : vous pouvez utiliser l’algorithme de Kruskal à travers différents langages de programmation, comme C++, Python, Java, C#, Javascript, etc.
Approfondissez vos connaissances en Machine Learning avec DataScientest