Si vous vous êtes déjà intéressé aux méthodes de réduction de dimension, vous avez sûrement étudié l'Analyse en Composantes Principales ou ACP. Dans cet article, nous allons nous intéresser à l’une des autres méthodes de réduction de dimension qui existe : t-SNE pour t-distributed Stochastic Neighbor Embedding. Cet algorithme propose une approche différente de l’ACP.
t-SNE est une technique de réduction de dimension utilisée en exploration de données de grandes dimensions développée en 2008 par Geoffrey Hinton et Laurens van der Maaten. Comme pour l’ACP l’objectif est de déterminer un espace de plus petite dimension tout en préservant les distances entre les points.
t-SNE et ACP
L’analyse en composantes principales est une méthode largement utilisée en réduction de dimension qui cherche à représenter les données dans un hyperplan proche de sorte à conserver au maximum la variance du nuage de données. En d’autres termes, il s’agit de représenter les données dans un sous-espace de plus petite dimension maximisant l’inertie totale du nuage projeté dans cet espace. Si vous voulez en savoir plus sur l’ACP, regardez notre vidéo à ce sujet :
Le Principe du t-SNE
L’algorithme t-SNE consiste à créer une distribution de probabilité qui représente les similarités entre voisins dans un espace en grande dimension et dans un espace de plus petite dimension. Par similarité, nous allons chercher à convertir les distances en probabilités. Il se découpe en 3 étapes :
- Étape 1 : Nous calculons les similarités des points dans l’espace initial en grande dimension. Pour chaque point xi nous centrons une distribution gaussienne autour de ce point. Ensuite nous mesurons, pour chaque point xj (i différent de j), la densité sous cette distribution gaussienne précédemment définie. Enfin, nous normalisons pour chacun des points. Nous obtenons ainsi une liste de probabilités conditionnelles notées :
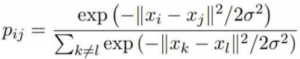
L’écart type se définit suivant une valeur appelée perplexité qui correspond au nombre de voisins autour de chaque point. Cette valeur est fixée par l’utilisateur à l’avance et permet d’estimer l’écart type des distributions gaussiennes définies pour chaque point xi. Plus la perplexité est grande, plus la variance est grande.
- Etape 2 : Nous avons besoin de créer un espace de plus petite dimension dans lequel nous allons représenter nos données. Évidemment au début nous ne connaissons pas les coordonnées idéales sur cet espace. Nous allons donc répartir aléatoirement les points sur ce nouvel espace. Le reste est assez similaire à l’étape 1, nous calculons les similarités des points dans l’espace nouvellement créé, mais en utilisant une distribution t-Student et non pas Gaussienne. De la même manière nous obtenons une liste de probabilités notées :
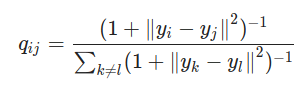
- Etape 3 : Pour représenter fidèlement les points dans l’espace de dimension plus petite nous aimerions, dans l’idéal, que les mesures de similarité dans les deux espaces coïncident. Nous avons donc besoin de comparer les similarités des points dans les deux espaces en utilisant la mesure Kullback_Leibler (KL). Nous cherchons ensuite à la minimiser par descente de gradient pour obtenir les meilleurs yi possibles dans l’espace de petite dimension. Cela revient à minimiser l’écart entre les distributions de probabilités entre l’espace d’origine et l’espace de plus petite dimension.
Comparaison des méthodes ACP et t-SNE
Pour mieux saisir les différences entre les deux méthodes ACP et t-SNE, considérons le jeu de données MNIST. Pour chacune des deux méthodes, nous avons représenté les données dans un espace à deux dimensions.
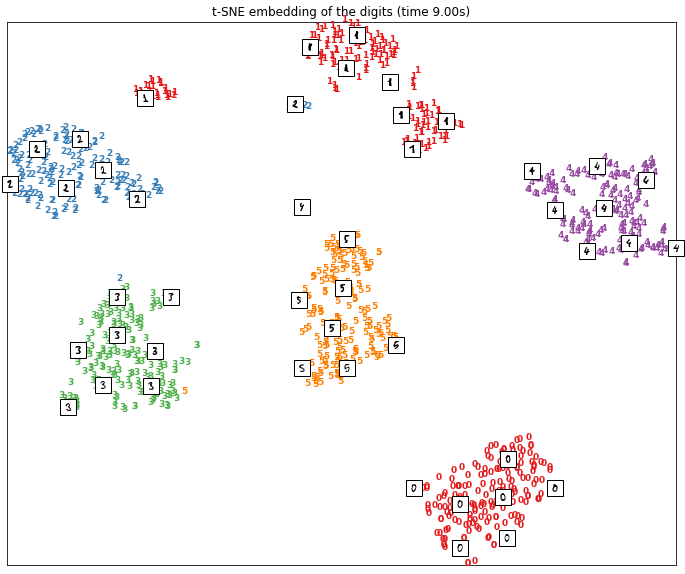
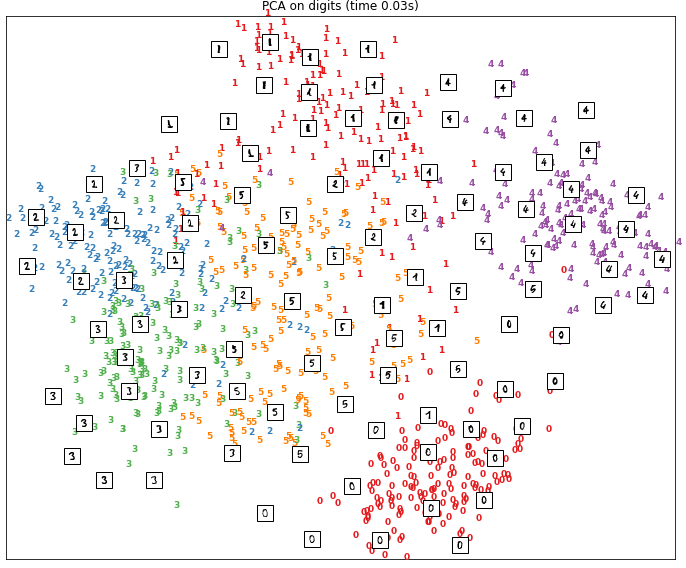
Sur la première figure, nous avons le résultat obtenu par réduction de dimension avec la méthode t-SNE. Sur la deuxième, nous avons le résultat obtenu avec une analyse en composantes principales.
Il est clair que TSNE a réussi à regrouper les données proches et éloigner les données dissemblables. Les points sont représentés en grappe, chacune des grappes correspondant à un chiffre entre 1 et 6.
Pour les résultats de l’ACP la séparation des données dans l’espace en 2 dimensions est beaucoup moins nette. Nous pouvons voir, que pour certains chiffres comme 0 les points correspondants sont bien regroupés entre eux. Cependant, pour d’autres chiffres comme les points associés au chiffre 5 ils sont répartis de manière plus diffuse.
Si vous souhaitez vous former sur des sujets comme les techniques de réduction de dimension, venez découvrir nos formations en format bootcamp ou bien continu !










