La corrélation est un outil statistique utilisé pour le Machine Learning afin d’identifier des relations de dépendance entre plusieurs variables. Il existe plusieurs types de corrélations. Découvrez ci-dessous plus de détails sur les corrélations de Pearson et de Spearman.
Pour l’analyse de données, un Data Scientist dispose de plusieurs outils statistiques. Parmi ces outils, il peut utiliser la corrélation. Il s’agit d’une mesure statistique particulièrement utile qui permet d’étudier la relation entre deux variables à partir du calcul d’un coefficient de corrélation. La corrélation correspond à la force (indiquée par la valeur absolue du coefficient) ainsi qu’à la direction (indiquée par la signe du coefficient) de la relation entre ces variables. La direction peut être soit positive (lorsqu’une x augmente, y augmente aussi) ou négative (lorsque x augmente, y diminue ou l’inverse). Il existe plusieurs types de corrélations. Parmi ces corrélations, il y en a deux qui sont particulièrement utilisées : la corrélation de Pearson et la corrélation de Spearman. Ces deux types de corrélations vont être détaillés dans la suite de cet article.
La corrélation de Pearson
La corrélation de Pearson, aussi appelée corrélation linéaire, permet de mesurer la relation linéaire entre deux variables continues. La corrélation de Pearson est indiquée par la valeur du coefficient de corrélation r calculée à l’aide de la formule suivante :
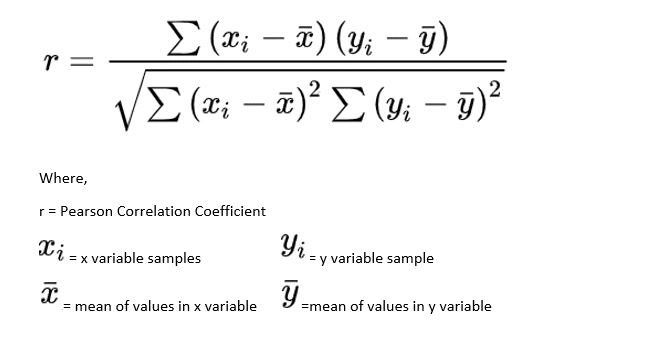
Avant de calculer le coefficient de Pearson, il faut s’assurer que les données vérifient les hypothèses suivantes :
- L’échantillon de données est aléatoire (représentatif de la population)
- Les variables sont quantitatives (continues)
- Les données sont associées par paires (on associe à chaque valeur x, une valeur y)
- Les observations sont indépendantes
- Les données sont distribuées normalement
- Il existe une relation linéaire entre les variables
- Aucun outlier n’est présent dans les données
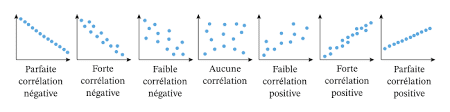
La valeur du coefficient de corrélation r est comprise entre -1 et 1. Il y a plusieurs cas possibles selon la valeur de r :
- Si r est proche de 1, alors les variables sont dépendantes linéairement positivement.
- Si r est proche de 0, alors il n’y a aucune relation linéaire entre les variables
- Si r est proche de -1, alors les variables sont dépendantes linéairement négativement.
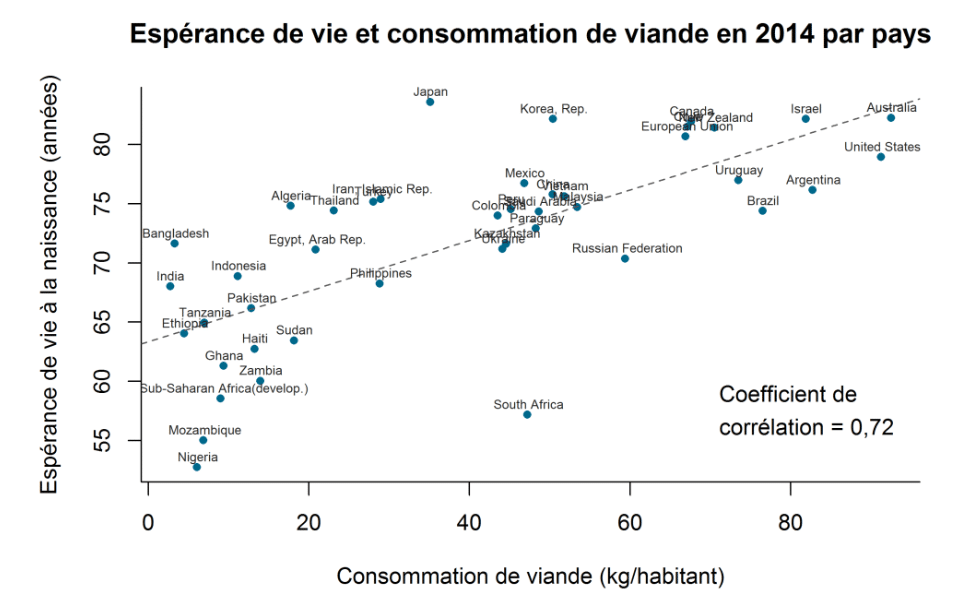
Un exemple d’application de la corrélation de Pearson serait par exemple l’étude de la relation entre la consommation de viande et l’espérance de vie selon le pays.
La corrélation de Spearman
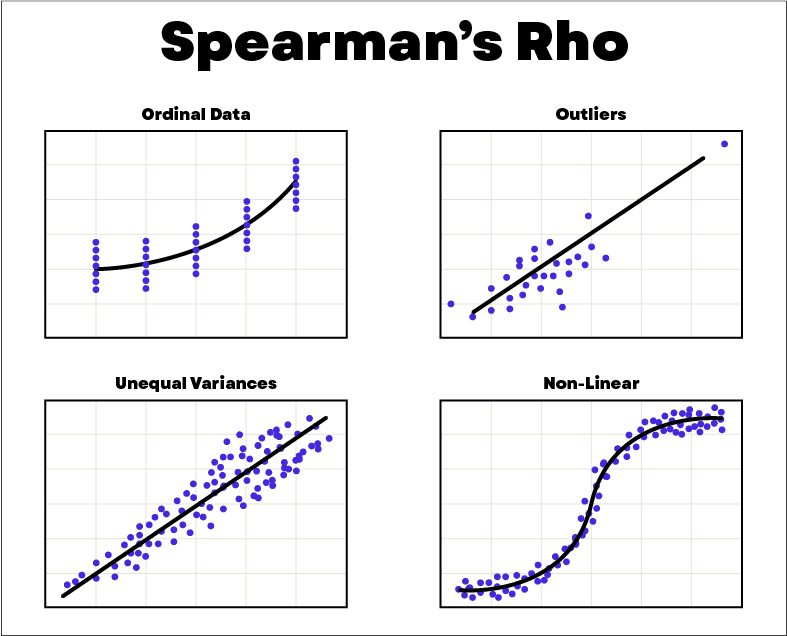
La corrélation de Spearman est une mesure de corrélation qui mesure une relation de monotonie entre deux variables à partir du rang des données. Un exemple de détermination du rang des données est : [58,70,40] devient [2,1,3]. On utilise souvent la corrélation de Spearman pour des données constituées d’outliers. Afin de mesurer la corrélation de Spearman, l’indicateur utilisé est le coefficient de Spearman rs aussi appelé coefficient de rang indiquée par la formule ci-dessous. Dans cette formule, la variable n indique le nombre de points de la série de données. La variable d correspond au carré de la différence des rangs entre chaque point de coordonnées (x,y).
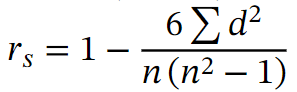
Avant de calculer le coefficient de Spearman, il faut s’assurer que les données vérifient les hypothèses suivantes :
- L’échantillon de données est aléatoire
- La relation entre les variables est monotone
- Les données sont associées par paires
- Les observations sont indépendantes
- Il existe une relation de monotonie entre les variables
- Les variables sont ordinales ou continues.
L’interprétation du coefficient de Spearman rs varie selon les valeurs obtenues :
- Si rs est proche de 1, alors il y a une relation monotone positive entre les variables.
- Si rs est proche de 0 alors il n’y a aucune relation monotone entre les variables
- Si rs est proche de -1 alors, il y a une relation monotone négative entre les variables.
Un exemple d’application de la corrélation de Spearman serait l’étude de la relation entre les préférences d’un consommateur et le prix du produit.
Conclusion
Les corrélations de Spearman et de Pearson sont deux mesures de corrélation différentes qui s’appliquent dans des situations spécifiques. La corrélation de Spearman utilise le rang des données pour mesurer la monotonie entre des variables ordinales ou continues. La corrélation de Pearson quant à elle détecte des relations linéaires entre des variables quantitatives avec des données suivant une distribution normale. Dans le cas d’un problème de Machine Learning, il est souvent question d’utiliser des matrices de corrélation constituées des coefficients de corrélations entre l’ensemble des variables d’un jeu de données. La notion de corrélation est donc importante pour le Machine Learning.
Si vous souhaitez vous former au Machine Learning pour aller plus en profondeur sur le domaine de la data science, n’hésitez pas à consulter nos formations de Data Scientist et Data Analyst.