Der zentrale Grenzwertsatz bekräftigt die Bedeutung der Normalverteilung und gehört zu den wichtigsten Konzepten der Statistik.
Aber was genau ist das? Wie wird es angewendet? Und vor allem: Wie wird es angewendet? Das wollen wir in diesem Artikel herausfinden.
Der zentrale Grenzwertsatz und die Konvergenz zur Normalverteilung
Der zentrale Grenzwertsatz besagt, dass eine Reihe von Variablen, die auf demselben Raum definiert sind, gegen eine reduzierte zentrierte Normalverteilung konvergiert.
💡Anders ausgedrückt: Je mehr unabhängige und identisch verteilte Zufallsvariablen addiert werden, desto mehr nähert sich die Wahrscheinlichkeitsverteilung der neuen Variablen einer Normalverteilung (auch Gaußsche Kurve oder Glockenkurve genannt). Dies gilt für alle Arten von Wahrscheinlichkeitsverteilungen eines Zufallsereignisses, wie z. B. die kontinuierliche Gleichverteilung, die Dreiecksverteilung, die Exponentialverteilung etc.
Sobald dieses Ereignis oft genug wiederholt wird, konvergiert sein Mittelwert allmählich zu einer Normalverteilung. Selbst wenn die Verteilung anfangs (nach ein- oder zweimaliger Addition der Variablen) noch nicht normal war, wird sie mit zunehmender Addition der Variablen allmählich normal.
Es ist genau dieses Prinzip, das es Statistikern ermöglicht zu behaupten, dass die Normalverteilung das Gesetz der Naturphänomene ist.
Ein wenig Geschichte: Der zentrale Grenzwertsatz entstand bereits 1718 dank De Moivre, der die Bedeutung der Normalverteilung nachwies. Aber erst mit den Arbeiten von Pierre-Simon de Laplace im Jahr 1812 wurde der Satz wirklich auf spezielle Fälle angewendet. Erst 1920 wurde es durch George Pólya („Über den zentralen Satz der Wahrscheinlichkeitsrechnung, unter denen, die sich auf den Begriff des Grenzwertes beziehen, und das Problem der Momente“) als zentraler Grenzwertsatz bezeichnet.
Die mathematische Anwendung des zentralen Grenzwertsatzes
Um den zentralen Grenzwertsatz zu berechnen, betrachte :
- X1, X2, … : als eine Folge von unabhängigen und identisch verteilten reellen Zufallsvariablen.
- σ ≠ 0: Der Erwartungswert μ und die Standardabweichung σ der D-Verteilung sind nicht unendlich.
- Sn = X1+X2+X3 … : wie die Summe aller Zufallsvariablen.
- nμ: entspricht dem Erwartungswert von Sn.
- σ√n: entspricht der Standardabweichung von Sn.
Der zentrale Grenzwertsatz besagt :
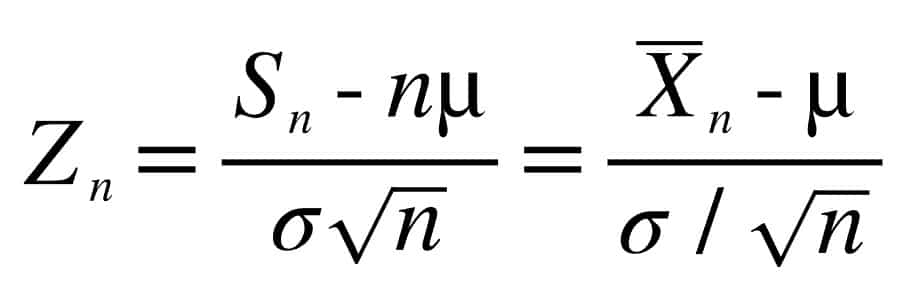
Hier ist der Erwartungswert von Znva 0 und die Standardabweichung 1. Mit anderen Worten: Die Variable ist zentriert und reduziert.
Zn tendiert also zur zentrierten reduzierten Normalverteilung, wenn n gegen unendlich geht.
Für jede reelle Zahl z :
lim n→∞ P (Zn ≤ z) = Φ(z).
wobei: Φ die Verteilungsfunktion von Ν(0,1) ist.
Beispiel für die Anwendung des zentralen Grenzwertsatzes
Um dir zu helfen, den Satz vom zentralen Grenzwert besser zu verstehen, hier ein konkretes Beispiel.
Marine und Julien würfeln. Jedes Mal, wenn sie auf eine gerade Zahl fallen, gewinnen sie 1 €, und jedes Mal, wenn sie auf eine ungerade Zahl fallen, verlieren sie 1 €. In diesem Fall sind die geraden und ungeraden Zahlen identisch verteilte Zufallsvariablen, denn Marine und Julien haben die gleiche Chance zu gewinnen wie zu verlieren. In den ersten Spielen kann es sein, dass die Waage mehr zu den geraden Zahlen (und damit zu den Gewinnen) oder zu den ungeraden Zahlen (und damit zu den Verlusten) ausschlägt. Aber im Laufe des Spiels geht die Wahrscheinlichkeit, dass sie gewinnen oder verlieren, gegen 0.
Dieser zentrale Grenzwertsatz findet sich in vielen Fällen des täglichen Lebens. Zum Beispiel die Größe und das Gewicht von Individuen innerhalb einer Population, die Verteilung der Gehälter innerhalb eines Unternehmens, … Der Durchschnitt dieser Ergebnisse ähnelt am Ende immer einer Glockenkurve, je größer die Stichprobe der Population wird,
Aufgrund der Vielzahl dieser Anwendungen ist der zentrale Grenzwertsatz ein unverzichtbares statistisches Werkzeug für Datenwissenschaftler, da er ihnen die Modellierung von Machine-Learning-Modellen ermöglicht. Neben den Werkzeugen der Datenwissenschaft müssen also auch die mathematischen Konzepte beherrscht werden. Genau aus diesem Grund ist eine Ausbildung unerlässlich. Entdecke unsere Programme.
Was du dir merken solltest
- Identisch verteilte Zufallsvariablen folgen einer Normalverteilung, wenn sie addiert werden.
- Mit dieser Aussage unterstreicht der zentrale Grenzwertsatz die Bedeutung der Normalverteilung.
- Der Satz gilt für eine Vielzahl von Hypothesen, von einem Glücksspiel bis hin zur Bestimmung des Durchschnittslohns oder der Bevölkerungsgröße.