Hast du Daniel vermisst? Das trifft sich gut, wir nämlich auch! Heute beantwortet unser, durch die Data Science Weiterbildung Schüler begleitende Experte diese Frage: Wie funktionieren rekurrente neuronale Netze?
Wenn du Fan unseres Blogs bist, weißt du bereits, was ein neuronales Netz ist (falls nicht, zögere nicht, diesen Artikel vorher zu lesen), aber was bringt das Adjektiv rekurrent zu diesem Modell? In diesem Artikel werden wir uns damit befassen, wie rekursive neuronale Netze, kurz RNN genannt, zu einem klassischen Modell im Deep Learning geworden sind.
Einige Anwendungen eines RNN
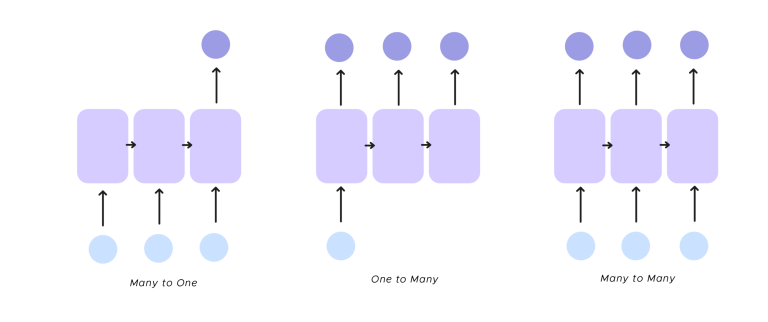
- one to many Die RNN erhält eine einzige Eingabe und gibt mehrere Ausgaben zurück,
das klassische Beispiel für dieses Verfahren ist die Bildunterschrift
- many to one Man hat mehrere Eingaben und es gibt nur eine Ausgabe. Ein Beispiel für diesen Modus ist die Gefühlsanalyse von Texten. Dabei wird ein Gefühl aus einer Gruppe von Wörtern identifiziert und das Wort bestimmt, das fehlt, um den Satz zu beenden, den du als Eingabe erhalten hast. Um mehr über die Gefühlsanalyse zu erfahren, besuche diesen Artikel.
- many to many Schließlich können wir mehrere Eingaben nehmen und mehrere Ausgaben erhalten. Wir haben nicht unbedingt die gleiche Anzahl an Input- und Output-Neuronen. Wir können hier die Übersetzung eines Textes nennen, aber wir können auch ehrgeizig sein und planen, ein Musikwerk mit seinem Anfang zu beenden.
Perfekt, wir haben gesehen, wie ein RNN funktioniert und wie viele Anwendungen es gibt, aber ist es auch perfekt? Leider hat es einen großen Nachteil, das sogenannte Kurzzeitgedächtnis, für das wir ein Beispiel aus dem Bereich TALN (Automatische Verarbeitung natürlicher Sprache) sehen werden.
Ist der RNN ein Goldfisch?
Nehmen wir den Fall der Satzvervollständigung.
Ich liebe Sushi und werde es in …
Der RNN kann sich das Wort Sushi nicht merken, um Japan vorherzusagen, weil er sich das Wort Sushi nicht gemerkt hat. Um es zu schaffen, Japan zu bestimmen, muss der RNN ein stärkeres Gedächtnis haben. Dies können wir erreichen, indem wir die Neuronen komplexer machen. Insbesondere werden wir uns den Fall des LSTM(Long Short Term Memory) ansehen. Zusätzlich zum herkömmlichen versteckten Zustand h_t werden wir einen zweiten Zustand namens c_t hinzufügen. Hier steht h_t für das Kurzzeitgedächtnis des Neurons und c_t für das Langzeitgedächtnis.
💡Auch interessant:
Wir wollen hier nicht auf die technischen Überlegungen zu diesem erschreckenden Schema eingehen. Das Wichtigste ist, dass wir eine viel komplexere Zelle haben, die es uns ermöglicht, das Speicherproblem zu lösen. Mit dem LSTM lassen wir h_t und c_t durch Gatter laufen, von denen es vier gibt.
- Das erste Tor entfernt unnötige Informationen, es ist das forget gate.
- Das zweite Tor, speichert die neue Information, das store gate.
- Das dritte Tor aktualisiert die Informationen, die wir dem RNN geben werden, mit dem Ergebnis des forget gate und des store gate, es ist das update gate.
- Das letzte Tor (output gate) gibt uns y_t und h_t.
Dieser langwierige Prozess ermöglicht es uns, die Informationen zu kontrollieren, die wir im Laufe der Zeit aufbewahren und weitergeben.
Der RNN kann dank seiner Lernfähigkeit herausfinden, was er behalten und was er vergessen sollte. LSTM (Long Short Term Memory) ist nicht einzigartig, wir können auch GRU (Gated Recurrent Unit) verwenden, nur die Architektur der Zelle ändert sich.
Fassen wir nun zusammen, was wir gesehen haben. RNNs sind eine besondere Art von neuronalen Netzen, die es ermöglichen, Daten zu verarbeiten, die nicht unabhängig sind und keine feste Größe haben. Dennoch sind Standard-RNNs durch das Problem des Kurzspeichers ziemlich eingeschränkt, das wir durch die Verwendung komplexerer Zellen wie LSTM oder GRU lösen können.
Es gibt eine Parallele zu einem anderen System neuronaler Netze: Convolutive Neuronal Networks (CNN). CNNs sind dafür bekannt, dass sie räumliche Informationen teilen, während RNNs zeitliche Informationen teilen. Du kannst mehr über CNNs in diesem Artikel erfahren. Wenn du RNNs in der Praxis anwenden möchtest, kannst du an unserem Data Scientist-Kurs teilnehmen.