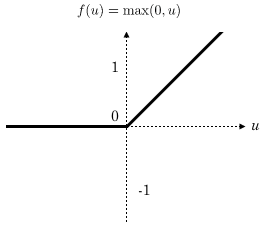Dans cette partie, nous allons nous focaliser sur un des algorithmes les plus performants du Deep Learning : les Convolutional Neural Network (CNN) ou réseaux de neurones convolutifs en français. Ce sont des modèles de programmation puissants permettant notamment la reconnaissance d’images en attribuant automatiquement à chaque image fournie en entrée, une étiquette correspondant à sa classe d’appartenance.
Bienvenue dans le troisième épisode de notre dossier Deep Learning. Après avoir introduit le Deep Learning et ses applications dans la première partie, nous nous sommes penchés sur la structure et le fonctionnement des réseaux de neurones dans la seconde. En route !
Quels sont les principales applications des CNN ?
Un réseau neuronal convolutif s’inspire de la nature, car la connectivité entre les neurones artificiels ressemble à l’organisation du cortex visuel animal.
L’un des principaux cas d’usage est la reconnaissance d’image. Les réseaux convolutifs apprennent plus rapidement et ont un meilleur taux d’erreur. Dans une moindre mesure, on les utilise aussi pour l’analyse vidéo.
Ce type de réseau est aussi utilisé pour le traitement naturel du langage. Les modèles CNN sont très efficaces pour l’analyse sémantique, la modélisation de phrase, la classification ou la traduction.
Par rapport à des méthodes traditionnelles comme les réseaux de neurones récurrents, les réseaux de neurones à convolution peuvent représenter différentes réalités contextuelles du langage qui ne reposent pas sur une hypothèse de séquence en série.
Les réseaux convolutifs ont aussi été utilisés pour la découverte de médicaments. Ils permettent d’identifier les traitements potentiels en prédisant les interactions entre molécules et protéines biologiques.
Les CNN ont notamment été utilisés pour les logiciels de jeu de Go ou de jeu d’échecs auxquels ils sont capables d’exceller. Une autre application est la détection d’anomalie sur une image en entrée (input).
Architecture d’un Convolutional Neural Network-CNN
Les CNN désignent une sous-catégorie de réseaux de neurones et sont à ce jour un des modèles de classification d’images réputés être les plus performant.
Leur mode de fonctionnement est à première vue simple : l’utilisateur fournit en entrée une image sous la forme d’une matrice de pixels.
Celle-ci dispose de 3 dimensions :
- Deux dimensions pour une image en niveaux de gris.
- Une troisième dimension, de profondeur 3 pour représenter les couleurs fondamentales (Rouge, Vert, Bleu).
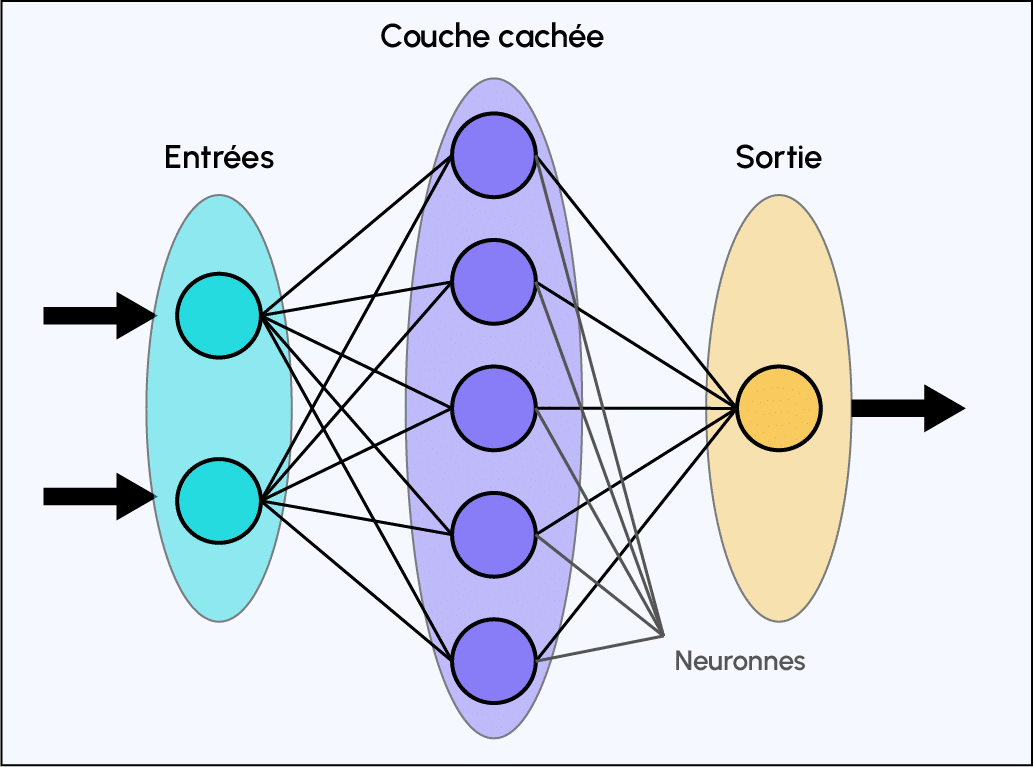
Contrairement à un modèle MLP (Multi Layers Perceptron) classique qui ne contient qu’une partie classification, l’architecture du Convolutional Neural Network dispose en amont d’une partie convolutive et comporte par conséquent deux parties bien distinctes :
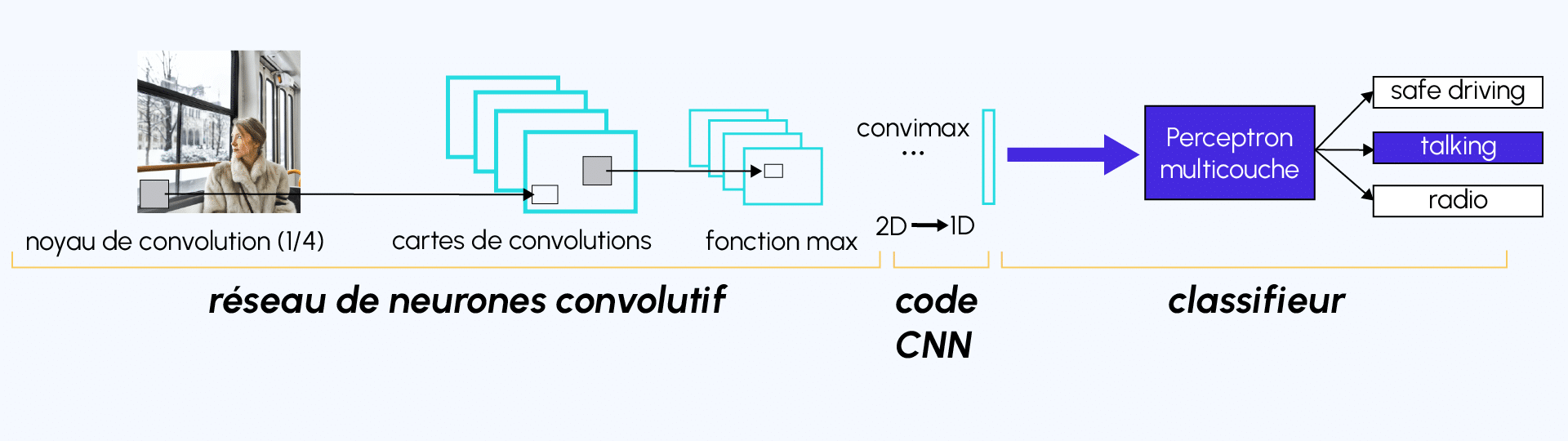
- Une partie convolutive : Son objectif final est d’extraire des caractéristiques propres à chaque image en les compressant de façon à réduire leur taille initiale. En résumé, l’image fournie en entrée passe à travers une succession de filtres, créant par la même occasion de nouvelles images appelées cartes de convolutions. Enfin, les cartes de convolutions obtenues sont concaténées dans un vecteur de caractéristiques appelé code CNN.
- Une partie classification : Le code CNN obtenu en sortie de la partie convolutive est fourni en entrée dans une deuxième partie, constituée de couches entièrement connectées appelées perceptron multicouche (MLP pour Multi Layers Perceptron). Le rôle de cette partie est de combiner les caractéristiques du code CNN afin de classer l’image. Pour revenir sur cette partie, n’hésitez pas à consulter l’article sur le sujet .
Partie convolutive : À quoi sert la convolution ?
Tout d’abord, à quoi sert la convolution ?
La convolution est une opération mathématique simple généralement utilisée pour le traitement et la reconnaissance d’images. Sur une image, son effet s’assimile à un filtrage dont voici le fonctionnement :
- Dans un premier temps, on définit la taille de la fenêtre de filtre située en haut à gauche.
- La fenêtre de filtre, représentant la feature, se déplace progressivement de la gauche vers la droite d’un certain nombre de cases défini au préalable (le pas) jusqu’à arriver au bout de l’image.
- À chaque portion d’image rencontrée, un calcul de convolution s’effectue permettant d’obtenir en sortie une carte d’activation ou feature map qui indique où est localisées les features dans l’image : plus la feature map est élevée, plus la portion de l’image balayée ressemble à la feature.
Exemple d’un filtre de convolution classique
Lors de la partie convolutive d’un Convolutional Neural Network, l’image fournie en entrée passe à travers une succession de filtres de convolution. Par exemple, il existe des filtres de convolution fréquemment utilisés et permettant d’extraire des caractéristiques plus pertinentes que des pixels comme la détection des bords (filtre dérivateur) ou des formes géométriques. Le choix et l’application des filtres se fait automatiquement par le modèle.
Parmi les filtres les plus connus, on retrouve notamment le filtre moyenneur (calcule pour chaque pixel la moyenne du pixel avec ses 8 proches voisins) ou encore le filtre gaussien permettant de réduire le bruit d’une image fournie en entrée :
Voici un exemple des effets de ces deux différents filtres sur une image comportant un bruit important (on peut penser à une photographie prise avec une faible luminosité par exemple). Toutefois, un des inconvénients de la réduction du bruit est qu’elle s’accompagne généralement d’une réduction de la netteté :
Comme on peut l’observer, contrairement au filtre moyenneur, le filtre gaussien réduit le bruit sans pour autant réduire significativement la netteté.
Outre sa fonction de filtrage, l’intérêt de la partie convolutive d’un CNN est qu’elle permet d’extraire des caractéristiques propres à chaque image en les compressant de façon à réduire leur taille initiale, via des méthodes de sous-échantillonnage tel que le Max-Pooling.
Méthode de sous échantillonnage : le Max-Pooling
Le Max-Pooling est un processus de discrétisation basé sur des échantillons. Son objectif est de sous-échantillonner une représentation d’entrée (image, matrice de sortie de couche cachée, etc.) en réduisant sa dimension. De plus, son intérêt est qu’il réduit le coût de calcul en réduisant le nombre de paramètres à apprendre et fournit une invariance par petites translations (si une petite translation ne modifie pas le maximum de la région balayée, le maximum de chaque région restera le même et donc la nouvelle matrice créée restera identique).
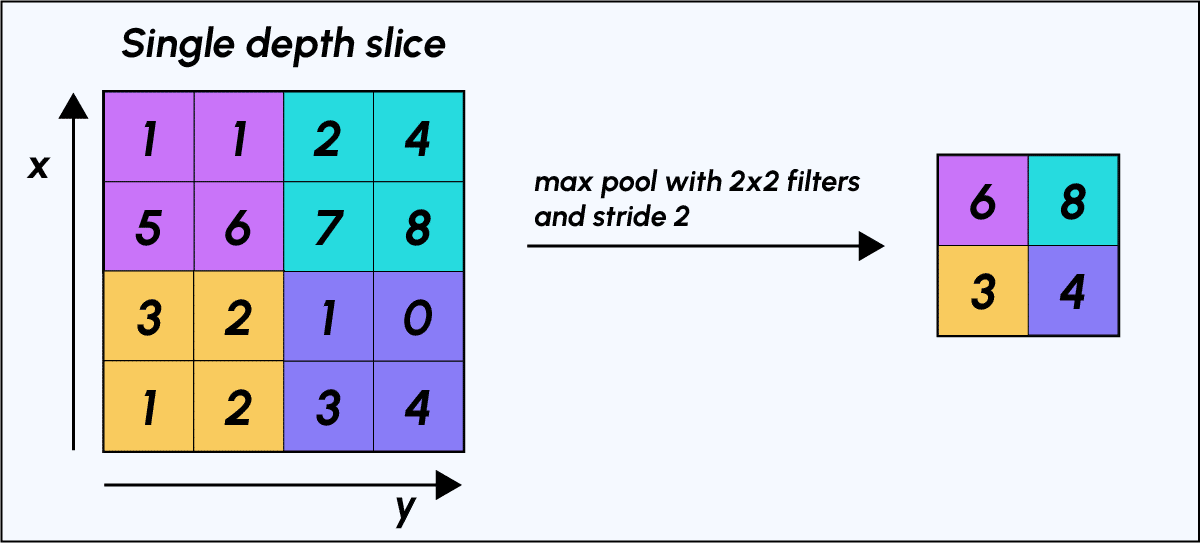
Pour rendre plus concret l’action du Max-Pooling, voici un exemple : imaginons que nous avons une matrice 4×4 représentant notre entrée initiale et un filtre d’une fenêtre de taille 2×2 que nous appliquerons sur notre entrée. Pour chacune des régions balayées par le filtre, le max-pooling prendra le maximum, créant ainsi par la même occasion une nouvelle matrice de sortie où chaque élément correspondra aux maximums de chaque région rencontrée.
Illustrons le processus :
La fenêtre de filtre se déplace de deux pixels vers la droite (stride/pas = 2) et récupère à chaque pas “l’argmax” correspondant à la valeur la plus grande parmi les 4 valeurs de pixels.
On comprend mieux l’utilité de la partie convolutive d’un CNN : contrairement à un modèle MLP classique, l’ajout en amont de la partie convolutive permet d’obtenir en sortie une « carte de caractéristiques » ou « code CNN » (matrice de pixels située à droite dans l’exemple) dont les dimensions sont plus petites que celles de l’image initiale ce qui va avoir l’avantage de diminuer grandement le nombre de paramètres à calculer dans le modèle.
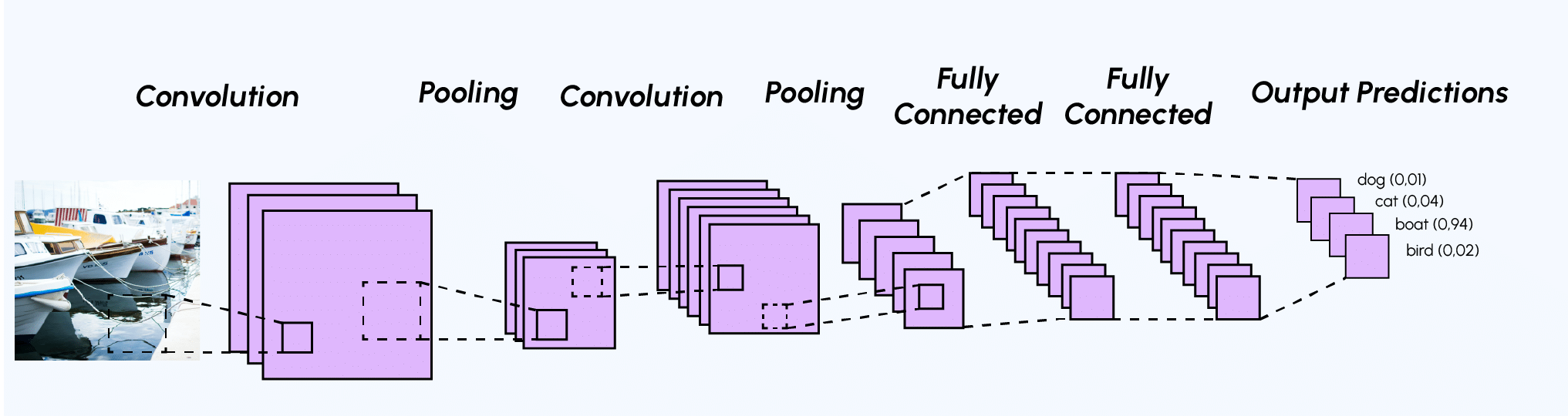
Exemple d’une architecture CNN et sa sortie
Après la partie convolutive d’un CNN, vient la partie classification. Cette partie classification, commun à tous les modèles de réseaux de neurones, correspondant à un modèle perceptron multicouche (MLP).
Son objectif est d’attribuer à chaque échantillon de données une étiquette décrivant sa classe d’appartenance.
L’algorithme que les perceptrons utilisent pour mettre à jour leurs poids (ou coefficients de réseaux) s’appelle la rétropropagation du gradient de l’erreur, célèbre algorithme de descente de gradient que nous verrons plus en détail par la suite .
Généralement, l’architecture d’un Convolutional Neural Network est sensiblement la même :
- Couche de convolution (CONV) : Le rôle de cette première couche est d’analyser les images fournies en entrée et de détecter la présence d’un ensemble de features. On obtient en sortie de cette couche un ensemble de features maps (cf plus haut : à quoi sert la convolution ?).
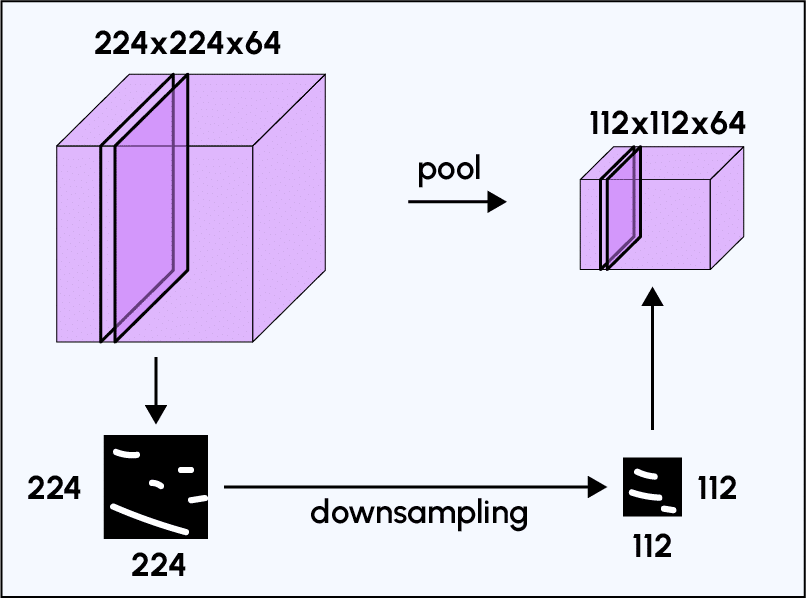
- Couche de Pooling (POOL) : La couche de Pooling est une opération généralement appliquée entre deux couches de convolution. Celle-ci reçoit en entrée les features maps formées en sortie de la couche de convolution et son rôle est de réduire la taille des images, tout en préservant leurs caractéristiques les plus essentielles. Parmi les plus utilisés, on retrouve le max-pooling mentionné précédemment ou encore l’average pooling dont l’opération consiste à conserver à chaque pas, la valeur moyenne de la fenêtre de filtre.
Finalement, on obtient en sortie de cette couche de Pooling, le même nombre de feature maps qu’en entrée mais considérablement compressées.
- La couche d’activation ReLU (Rectified Linear Units) : Cette couche remplace toutes les valeurs négatives reçues en entrées par des zéros. L’intérêt de ces couches d’activation est de rendre le modèle non linéaire et de ce fait plus complexe.
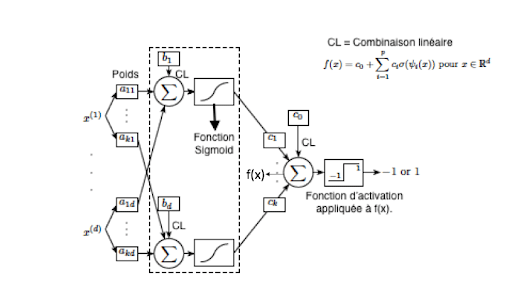
- Couche Fully Connected (FC) : Ces couches sont placées en fin d’architecture de CNN et sont entièrement connectées à tous les neurones de sorties (d’où le terme fully-connected). Après avoir reçu un vecteur en entrée, la couche FC applique successivement une combinaison linéaire puis une fonction d’activation dans le but final de classifier l’input image (voir schéma suivant). Elle renvoie enfin en sortie un vecteur de taille d correspondant au nombre de classes dans lequel chaque composante représente la probabilité pour l’input image d’appartenir à une classe.
Implémentation d’un CNN pré-entraîné sur Python :
Pour des usages pratiques et étant donné la complexité de création de performants CNN “fait à la main“, nous allons utiliser des réseaux pré-entraînés disponibles dans le module Torchvision. Voyons comment celui-ci peut être implémenté sur Python :
Mise en application d’un CNN : Identification d’images quelconques à partir du dataset ImageNet : dix millions d’images étiquetées
ImageNet est une base de données de plus de dix millions d’images étiquetées produit par l’organisation du même nom, à destination des travaux de recherche en vision par ordinateur.
Voici un extrait de ce volumineux dataset :
Étape 0 : Tout d’abord, importons toutes les librairies qui nous serons nécessaires pour la suite
Étape 1 : Entrainement du modèle pré-entrainé VGG16
Étape 2 : Importation des 3 images à prédire
Étape 3 : Prétraitement des images
Étape 4 : Prédiction du modèle
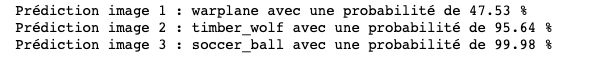
On peut également afficher les 5 labels jugés les plus probables par VGG16 :
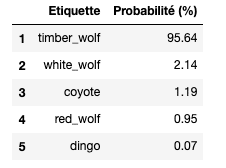
→ VGG16 a donc réussi à prédire avec une grande confiance (95,6%) que non seulement l’image donnée en entrée était un loup mais est même allé plus loin en précisant sa race à savoir ici un loup gris de l’Est (timber wolf). Impressionnant non ?
Finalement, le principe de fonctionnement d’un CNN est assez facile à comprendre, mais paradoxalement, la mise en place d’un tel procédé pour classifier des images demeure très complexe étant donné le nombre considérable de paramètres à définir : nombre, taille, déplacement des filtres, choix de la méthode de pooling, choix du nombre de couches de neurones, nombre de neurones par couches, etc.
Pour pallier à cet obstacle, Python à travers le module Torchvision, offre la possibilité d’exploiter des modèles CNN pré-entraînés performants tels que VGG16, Resnet101, etc.
Nous avons défini dans cet article le fonctionnement et l’architecture des Convolutional Neural Network, en nous concentrant sur sa spécificité: la partie convolutive.
Il nous reste encore à appréhender une étape de la classification : la rétropropagation du gradient de l’erreur, célèbre algorithme de descente de gradient. Ne vous inquiétez pas, un prochain épisode sur le sujet arrive bientôt sur le Blog !
Article 1 : Introduction au deep learning et aux réseaux de neurones
Article 2 : Convolutional neural network
Article 3 : Fonctionnement des réseaux de neurones
Article 4 : Transfer learning
