Quatrième épisode de notre série consacrée au Deep Learning, n’hésitez pas à lire ou relire les premiers pour vous rafraîchir la mémoire sur les définitions de Deep Learning, Machine Learning et Intelligence Artificielle ainsi que sur les grandes lignes du fonctionnement et des applications des réseaux de neurones. N'hésitez pas également à relire la partie dédiée au CNN : Convolutional Neural Network . Démarrons sans plus tarder cette nouvelle partie !
Table des matières:
Vous allez maintenant découvrir en détails comment les réseaux de neurones artificiels apprennent et leur manière de s’articuler dans un réseau.
Petit rappel sur les réseaux de neurones
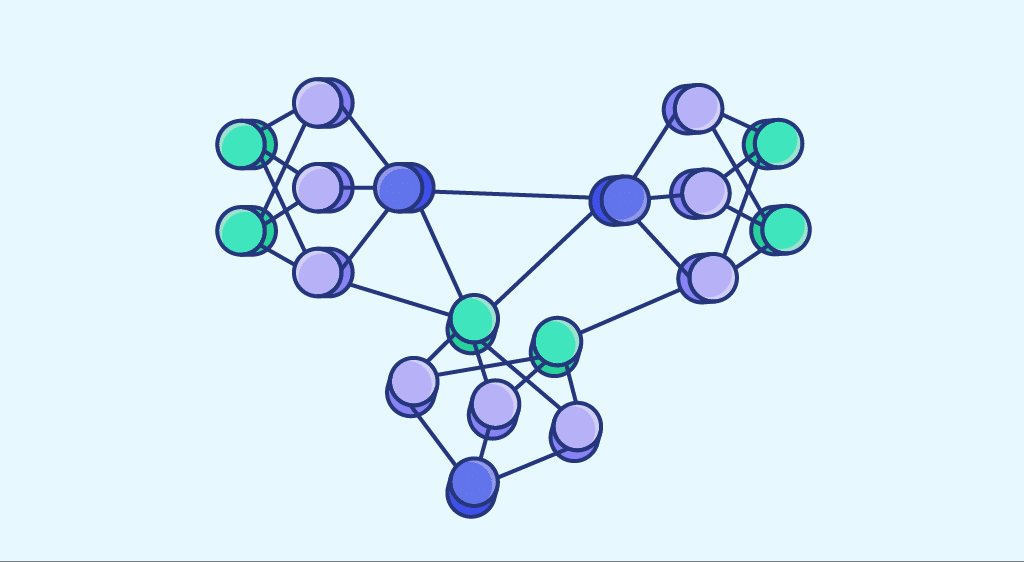
Pour rappel, les multi-layers perceptron sont un empilement de perceptron qui sont mis sous forme de couche. Prenons l’exemple suivant pour illustrer le concept :
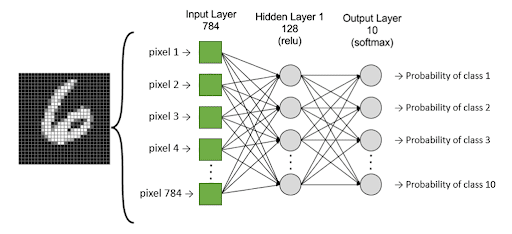
Le modèle consiste à classifier (en 10 classes) des images de chiffres manuscrits. Les carrés verts sont la couche d’entrée de notre modèle, c’est-à-dire la valeur des pixels. La couche intermédiaire et la couche sortie sont des perceptrons représentés par des ronds gris. La dernière couche possède 10 neurones puisqu’il y a 10 classes et retourne la probabilité correspondante à chaque classe.
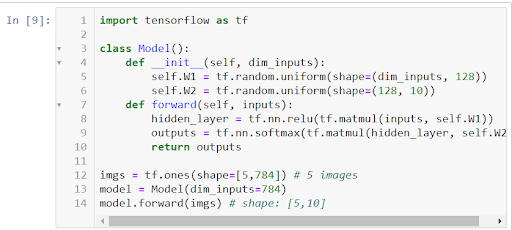
Nous pouvons très facilement implémenter le modèle sur TensorFlow :
Comment entraîner le modèle ?
Pour entraîner notre modèle, c’est-à-dire trouver les poids adaptés, il est nécessaire de définir une fonction qui va quantifier l’erreur de notre modèle . En général, pour les problèmes de classification, nous utilisons la fonction « cross-entropy » pour mesurer l’erreur.
Notre problème d’optimisation consiste à trouver les poids de notre modèle qui minimise notre fonction d’erreur :
J(w)En Deep Learning, nous sommes confrontés à des problèmes de minimisation complexe et sans solution explicite. C’est pourquoi, des méthodes d’optimisation comme la descente de gradient sont utilisée pour les résoudre.
Descente de gradient : Pour descendre, il faut aller vers le bas
Pour découvrir d’une manière intuitive le concept de descente du gradient, regardez notre vidéo sur le sujet :
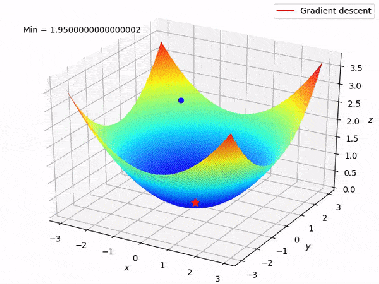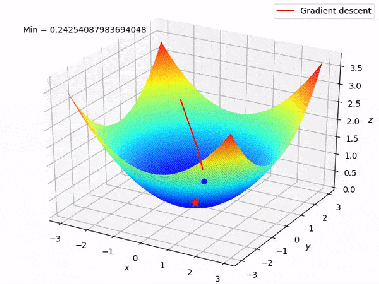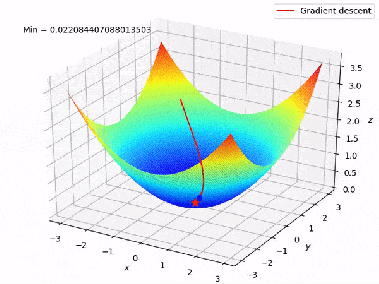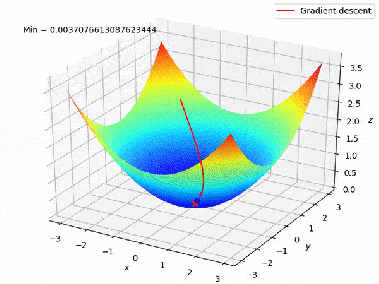
Dans notre cas, la fonction de perte (d’erreur) peut être vue comme une montagne où l’on recherche les coordonnées (poids de modèle) du point d’altitude minimale. Et, la valeur du gradient de la fonction de perte correspond à l’orientation et à l’inclinaison de la pente en un point donné :
- Si la norme du gradient est élevée, c’est que la pente est très raide.
- Si la norme du gradient est faible, c’est que la pente est peu inclinée.
- Si le gradient est nul, c’est qu’on se trouve sur un plat (minimum).
Par conséquent, la descendre de gradient consiste initialement à choisir les poids aléatoires, et de suivre l’inverse du gradient à chaque itération :
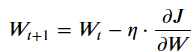
Avec :
- Wt : les paramètres de notre modèle
- η : pas du gradient, autrement dit, la vitesse d’apprentissage
- J : fonction de perte
Un pas de gradient trop grand ou trop petit ne permettra pas à l’algorithme MLP de converger vers une solution satisfaisante. Trouver le bon pas de gradient est tout le challenge du Deep Learning.
Pour résumer, le neurone artificiel autrement appelé le perceptron se comporte comme un modèle de classification linéaire. Le perceptron multicouche quant à lui lie et empile sous forme de couche les perceptrons pour apporter une plus grande complexité à l’établissement des règles.
Après avoir défini les paramètres du modèle, nous avons vu qu’il était nécessaire de quantifier l’erreur de celui-ci. Pour ce faire, le Deep Learning utilise principalement la descente de gradient pour ajuster ses poids de façon à minimiser la fonction de perte.
Pour explorer les mathématiques qui se cachent derrière cet algorithme de descente de gradient et l’importance du taux d’apprentissage découvrez cet article.
Dans la suite, nous allons vous présenter Le Transfer Learning, une catégorie d’apprentissage à succès utilisée en Deep Learning et qui semble fortement s’inspirer de l’apprentissage humain !
Article 1 : Introduction au deep learning et aux réseaux de neurones
Article 2 : Convolutional Neural Network
Article 3 : Fonctionnement des réseaux de neurones
Article 4 : Transfer Learning