Cet article est le premier d’une série consacrée au Deep Learning : Après avoir présenté dans les grandes lignes le fonctionnement et les applications des réseaux de neurones, vous découvrirez plus en détails dans les articles suivants les principaux types de réseaux et leurs architectures, ainsi que des méthodes et divers exemples d’applications du Deep Learning aujourd’hui. Démarrons sans plus tarder notre Introduction au Deep Learning.
Les concepts clés : IA, Machine Learning, et Deep Learning
Depuis quelques années, un nouveau lexique lié à l’émergence de l’intelligence artificielle dans notre société inonde les articles scientifiques, et il est parfois difficile de comprendre de quoi il s’agit. Lorsqu’on parle d’intelligence artificielle, on fait très souvent l’allusion aux technologies associées comme le Machine learning ou le Deep learning. Deux termes extrêmement utilisés avec des applications toujours plus nombreuses, mais pas toujours bien définis. Pour commencer, revenons sur ces trois définitions essentielles :
- L’intelligence artificielle : c’est un champ de recherche qui regroupe l’ensemble des techniques et méthodes qui tendent à comprendre et reproduire le fonctionnement d’un cerveau humain.
- Le Machine Learning : c’est un ensemble de techniques donnant la capacité aux machines d’apprendre automatiquement un ensemble de règles à partir de données. Contrairement à la programmation qui consiste en l’exécution de règles prédéterminées.
- Le Deep Learning ou apprentissage profond : c’est une technique de machine learning reposant sur le modèle des réseaux neurones: des dizaines voire des centaines de couches de neurones sont empilées pour apporter une plus grande complexité à l’établissement des règles.
Machine Learning : Apprentissage supervisé et non supervisé
Le Machine Learning est un ensemble de techniques donnant la capacité aux machines d’apprendre, contrairement à la programmation qui consiste en l’exécution de règles prédéterminées. Il existe deux principaux types d’apprentissages en Machine Learning. L’apprentissage supervisé et non supervisé.
En apprentissage supervisé, l’algorithme est guidé avec des connaissances préalables de ce que devraient être les valeurs de sortie du modèle. Par conséquent, le modèle ajuste ses paramètres de façon à diminuer l’écart entre les résultats obtenus et les résultats attendus. La marge d’erreur se réduit ainsi au fil des entraînements du modèle, afin d’être capable de l’appliquer à de nouveaux cas.
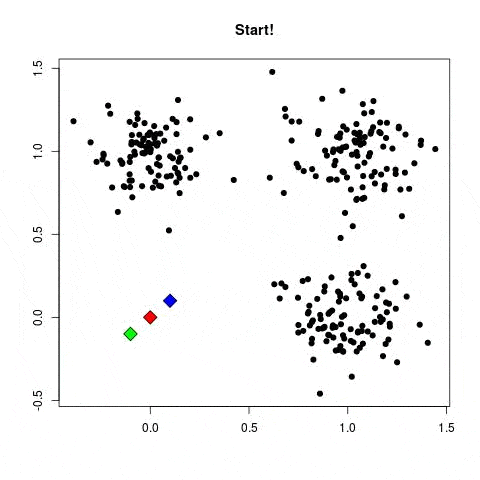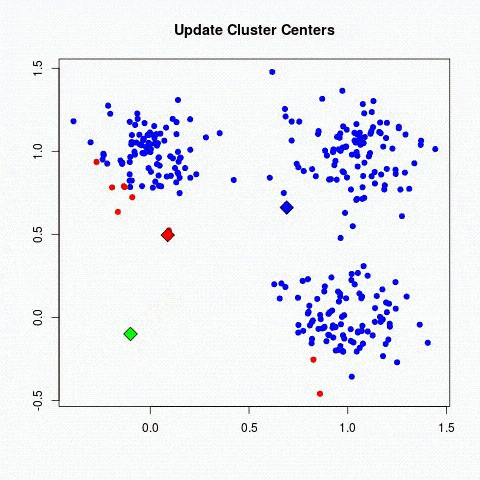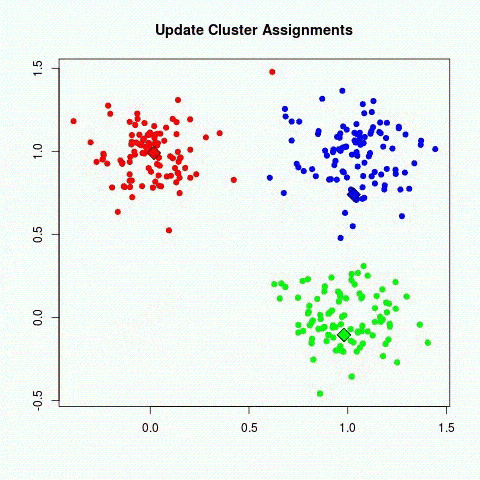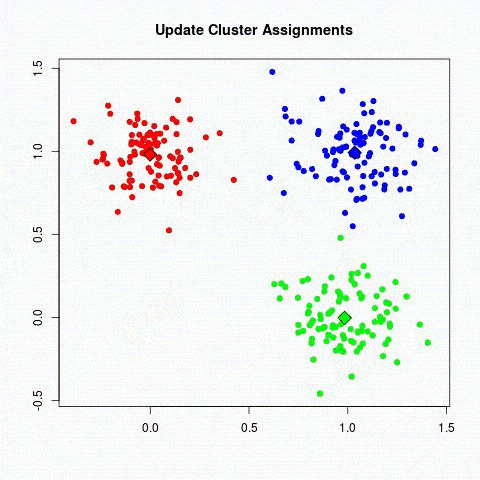
En revanche, l’apprentissage non supervisé n’utilise pas de données étiquetées. Il est alors impossible à l’algorithme de calculer de façon certaine un score de réussite. Son objectif est donc de déduire les regroupements présents dans nos données. Prenons l’exemple, d’un jeu de données de fleurs, on recherche à les regrouper en classes. Ici, nous ne connaissons pas l’espèce de la plante, mais nous voulons essayer de les regrouper, par exemple, si les formes des fleurs sont similaire alors elles sont en rapport avec une même plante correspondante.
Il existe deux principaux domaines de modèles dans l’apprentissage non-supervisées pour retrouver les regroupements :
- Les méthodes par partitionnement : les algorithmes des k-means.
- Les méthodes de regroupement hiérarchique : classification ascendante hiérarchique (CAH)
Qu'est-ce que le Deep Learning ?
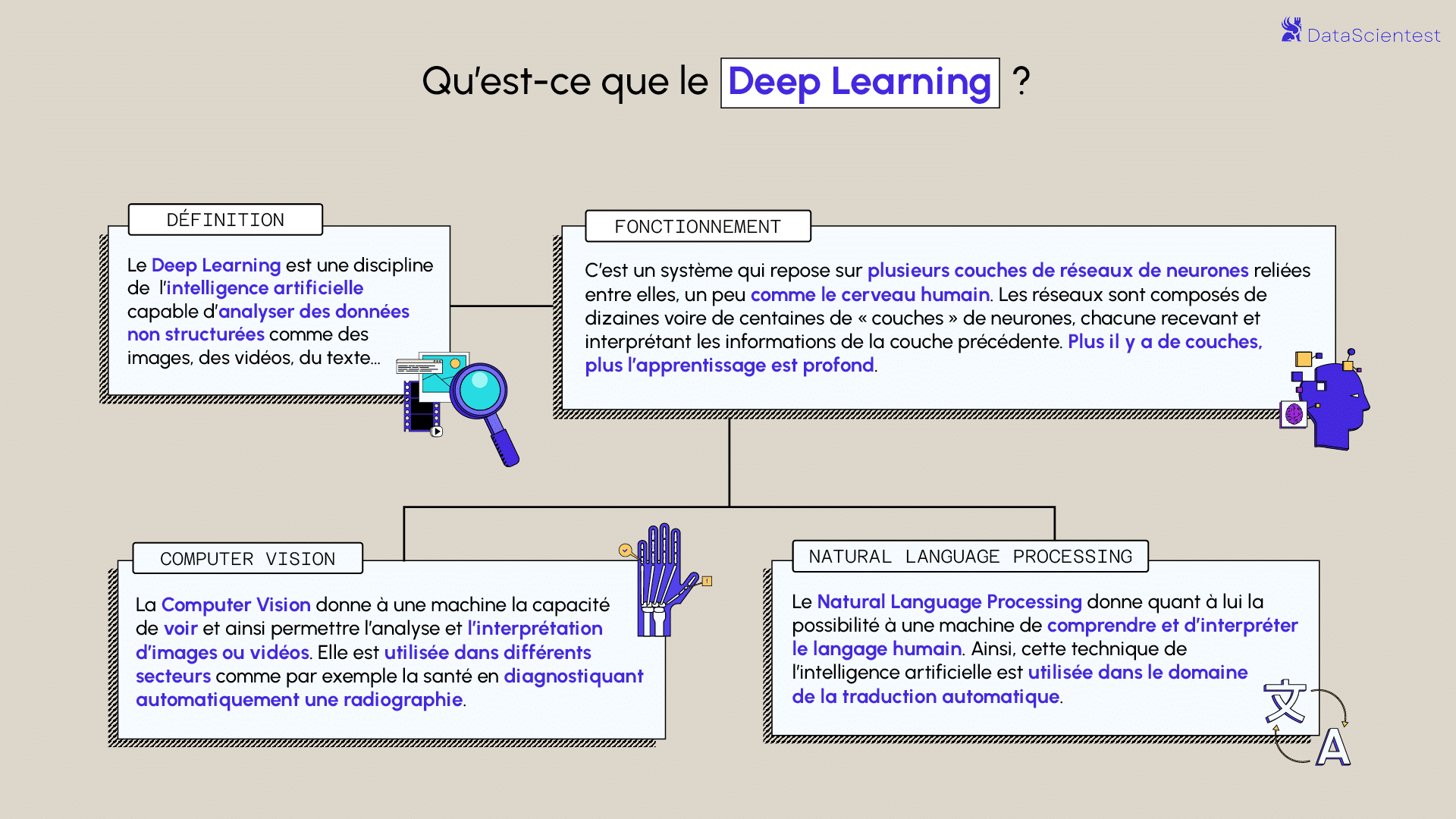
Le Deep learning ou apprentissage profond est l’une des technologies principales du Machine learning. Avec le Deep Learning, nous parlons d’algorithmes capables de mimer les actions du cerveau humain grâce à des réseaux de neurones artificielles. Les réseaux sont composés de dizaines voire de centaines de « couches » de neurones, chacune recevant et interprétant les informations de la couche précédente.
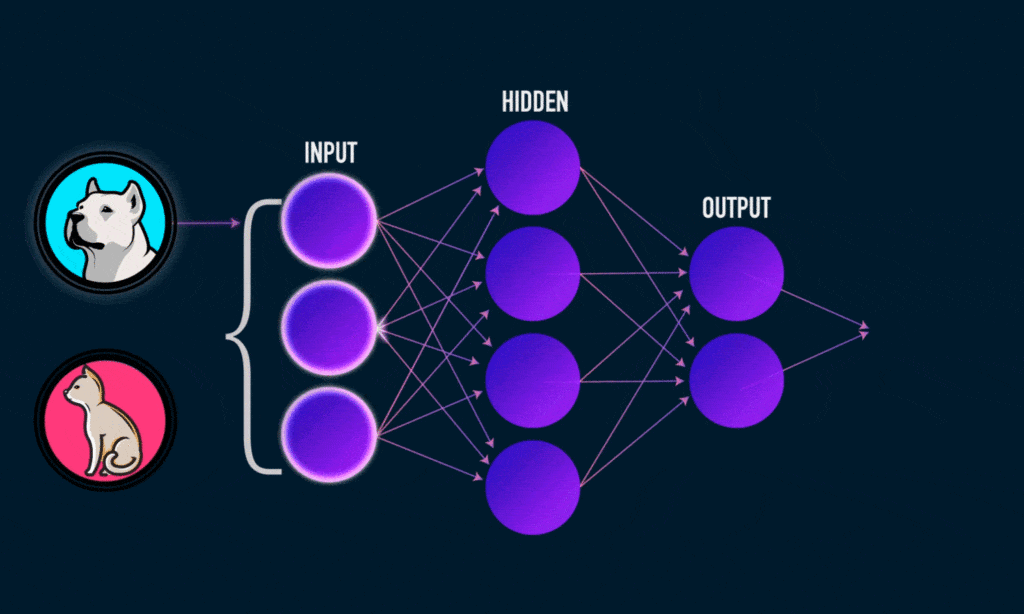
source : Medium.com
Chaque neurone artificiel représenté dans l’image précédente par un rond, peut être vu comme un modèle linéaire. En interconnectant les neurones sous forme de couche, nous transformons notre réseau de neurones en un modèle non-linéaire très complexe.
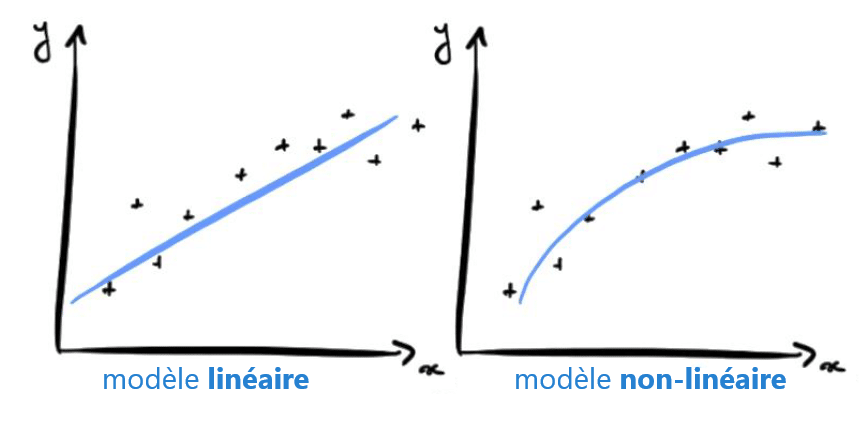
Pour illustrer le concept, prenons un problème de classification entre chien et chat à partir d’image. Lors de l’apprentissage, l’algorithme va ajuster les poids des neurones de façon à diminuer l’écart entre les résultats obtenus et les résultats attendus. Le modèle pourra apprendre à détecter les triangles dans une image puisque les chats ont des oreilles beaucoup plus triangulaires que les chiens.
A quoi sert le Deep Learning ?
Les modèles de Deep learning ont tendance à bien fonctionner avec une grande quantité de données alors que les modèles d’apprentissage automatique plus classique cessent de s’améliorer après un point de saturation.
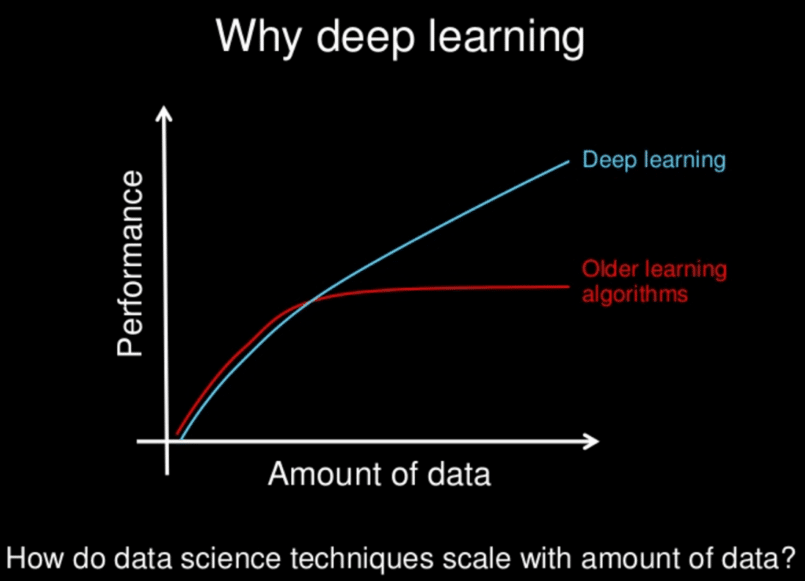
Au fil des années, avec l’émergence du big data et de composants informatiques de plus en plus puissant, les algorithmes de Deep Learning gourmands en puissance et en données ont dépassé la plupart des autres méthodes. Ils semblent être prêt à résoudre bien des problèmes : reconnaître des visages, vaincre des joueurs de go ou de poker, permettre la conduite de voitures autonomes ou encore la recherche de cellules cancéreuses.
L'IA dans le monde professionnel
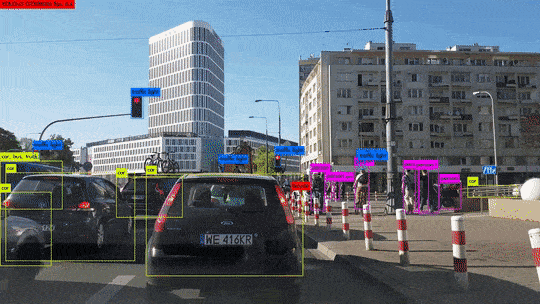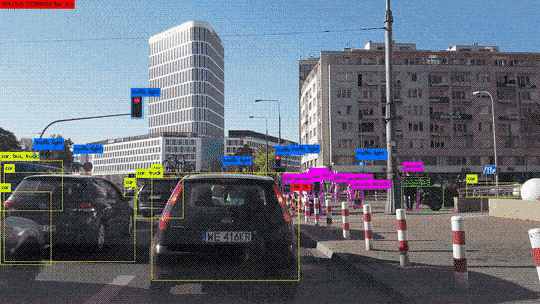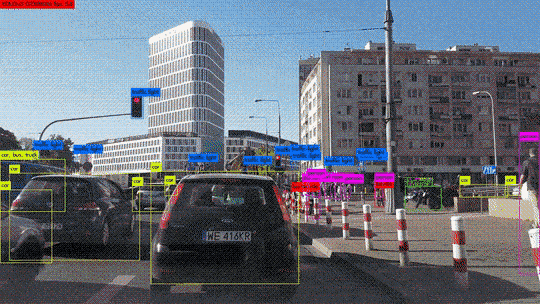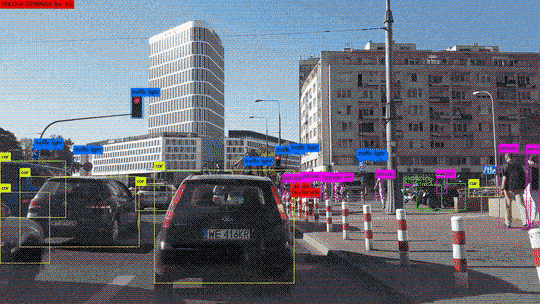
Le Deep Learning comme solution dans le e-commerce
Il est évident que le secteur du commerce électronique génère de grandes quantités de données. Les entreprises, les commerçants et les distributeurs sont conscients que les solutions de Big Data pour gérer leurs opérations rendront leur activité plus précieuse. Malgré l’irruption de toutes ces solutions innovantes, le Big Data peut représenter une bénédiction ou une malédiction, selon la façon dont il est utilisé et appliqué.
La révolution de l’intelligence artificielle vise à faciliter la gestion de cette énorme quantité de données, grâce à des technologies intelligentes comme le Deep learning. Elle est essentielle, car elle fournit des éléments pour une meilleure analyse des données.
Dans un cas pratique, l’analyse par l’IA permet à une boutique en ligne de proposer plus facilement des produits intéressants à ses clients, de mettre en évidence leurs préférences et de leur apporter une attention personnalisée. Pour ce faire, le Deep learning automatise ce que l’on appelle l’analyse prédictive. Grâce à cette dernière, les clients peuvent recevoir des suggestions lors d’un achat.
L’apprentissage profond définit un style lorsqu’il s’agit de faire du commerce électronique. En effet, il ne s’agit pas de créer des sites en ligne qui attirent de grandes proportions d’acheteurs. L’objectif est d’envoyer des messages clairs et individualisés à chacun d’eux.
Le Big Data est soumis à une analyse approfondie grâce au Deep learning, ce qui conduit à faciliter le processus d’achat des clients. Les algorithmes d’apprentissage en profondeur aident l’entreprise à obtenir une meilleure expérience et à garder une trace de ceux qui ont visité son site.
L’apprentissage profond arrive pour faciliter l’expansion du commerce électronique. Les ventes en ligne sont stimulées par les tendances technologiques telles que les chatbots.
D’une certaine manière, le Deep Learning redéfinit le commerce en ligne et on n’est qu’aux balbutiements. Par conséquent, ceux qui l’adoptent auront plus d’avantages.
Deep Learning et réseaux de neurones : biologiques ou artificiels ? Même combat
Avant de s’attaquer au fonctionnement précis des réseaux de neurones, on s’est dit qu’il serait intéressant de faire un parallèle avec les neurones biologiques .
(Pas de panique, un article dédié aux réseaux de neurones utilisés en Deep Learning suivra )
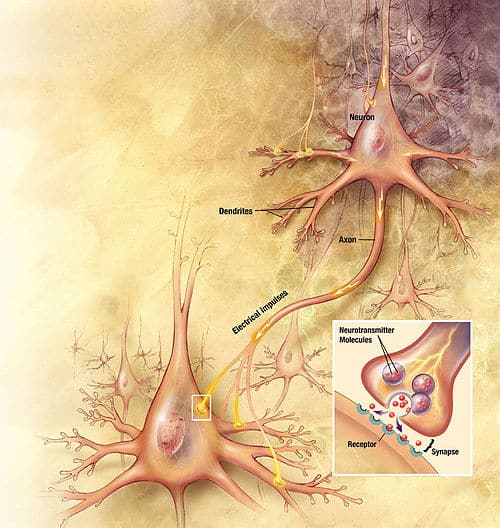
Neurone Biologique : Structure et rôle
Le système nerveux est composé de milliards de cellules : c’est un réseau de neurones biologiques. En effet, les neurones ne sont pas indépendants les uns des autres, ils établissent entre eux des liaisons et forment des réseaux plus ou moins complexes.
Le neurone biologique est composé de trois parties principales :
- Le corps cellulaire composé du centre de contrôle traitant les informations reçues par les dendrites.
- Les dendrites sont les principaux fils conducteurs par lesquels transitent l’information venue de l’extérieur.
- L’axone est fil conducteur qui conduit le signal de sortie du corps cellulaire vers d’autres neurones.
Quant aux synapses, elles font effet de liaison et de pondération entre neurones et permettent donc aux neurones de communiquer entre eux.
Quel est le lien entre les neurones biologiques et neurones artificiels ?
En résumé :
Les neurones biologiques disposent d’un centre de contrôle (appelé cellule somatique) faisant la somme des informations recueillies par les dendrites. Ensuite, le centre de contrôle retourne un potentiel d’action en suivant les règles suivantes :
- Si la somme en entrée ne dépasse pas le seuil d’excitation : pas de message nerveux via l’axone.
- Si la somme en entrée dépasse le seuil d’excitation : un message nerveux est émis via l’axone (c’est l’idée, mais en réalité un peu plus compliqué).
Procédons à une comparaison simple des étapes principales de l’algorithme du perceptron avec les éléments constitutifs des neurones biologiques. Ce choix d’algorithme se justifie car il se rapproche au mieux du fonctionnement des neurones biologiques :
- Les synapses/dendrites : pondération de chaque élément en entrée wi
xi
- Corps cellulaires : application d’une fonction d’activation f à la somme des entrées pondérées
- Axone : sortie de notre modèle

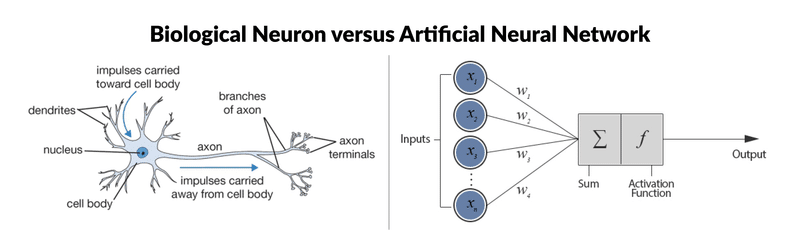
Le vocabulaire spécifique à cet algorithme est le suivant :
- Le vecteur w porte le nom de vecteur de poids (qui s’ajuste lors de l’entraînement).
- Le vecteur x porte le nom de vecteur d’entrée.
f porte le nom de fonction d’activation.
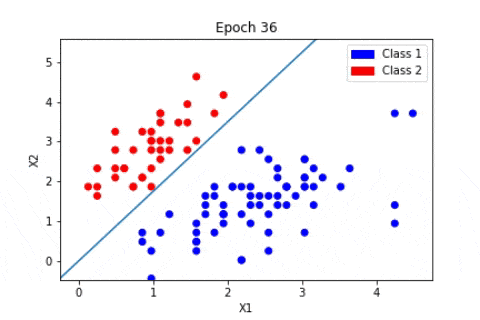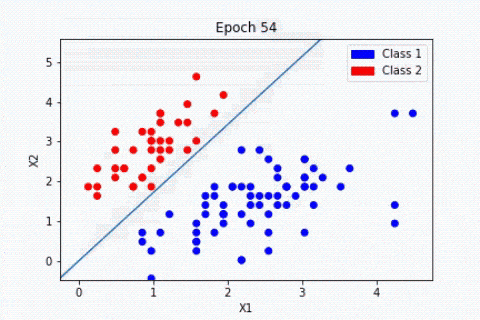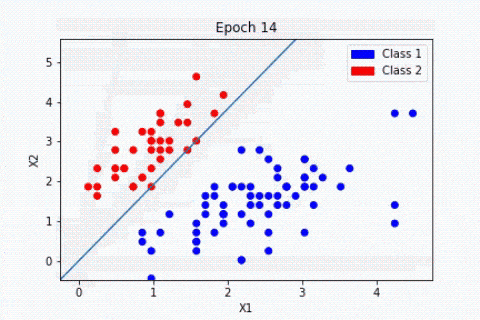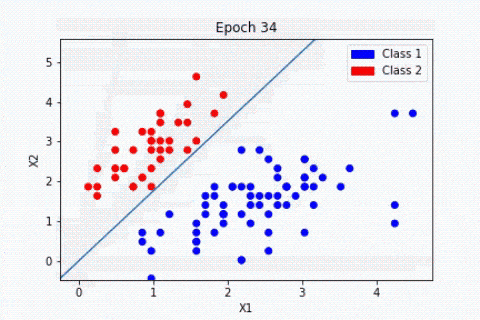
Pour la plupart des fonctions d’activations, le perceptron consiste à trouver l’hyperplan séparateur (définie par w) entre nos deux classes :
L’algorithme de Perceptron simple n’est plus utilisé en pratique puisque d’autres algorithmes comme le Support Vector Machine sont bien plus performants. De même, les neurones biologiques ne sont pas utilisés individuellement, ils sont généralement reliés à d’autres neurones.
L’intérêt de l’algorithme du Perceptron vient d’une technique démontrée en 1989 par George Cybenko qui consiste à lier et empiler des couches de perceptron pour apporter une plus grande complexité. Un algorithme de ce type s’appelle Perceptron Multicouche (Multilayer Perceptron en anglais), souvent abrégé par l’acronyme MLP.

Dans la figure précédente, le modèle consiste à classifier (en 10 classes) des images de chiffres manuscrits. Les carrés verts sont les entrées de notre modèle, les perceptrons sont représentés par des ronds gris et les liaisons sont représentées par les flèches.
En général, la dernière couche de notre modèle permet de mettre en forme le résultat souhaité. Ici, comme nous avons un problème de classification, nous recherchons alors à prédire la probabilité de chaque classe (chiffre 0, chiffre 1 …). C’est pour cet raison que la dernière couche possède 10 neurones puisqu’il y a 10 classes, et une fonction d’activation « softmax » permettant de retourner une probabilité.
C’est beaucoup plus libre pour les autres couches de notre modèle, il est surtout très important que les fonctions d’activations des perceptrons soient non-linéaires pour complexifier son modèle. En pratique, les fonctions d’activations tanh ou ReLU sont les plus utilisées.
Comme dans les LEGO, c’est au Data Scientist de choisir l’architecture de son modèle.
Article 1 : Introduction au Deep Learning et aux réseaux de neurones
Article 2 : Convolutional Neural Network
Article 3 : Fonctionnement des réseaux de neurones
Article 4 : Transfer Learning
Sources
- F. Rosenblatt (1958), The perceptron: a probabilistic model for information storage and organization in the brain (http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.335.3398&rep=rep1&type=pdf)
- G. Cybenkot (1989), Approximation by Superpositions of a Sigmoidal Function (http://cognitivemedium.com/magic_paper/assets/Cybenko.pdf)