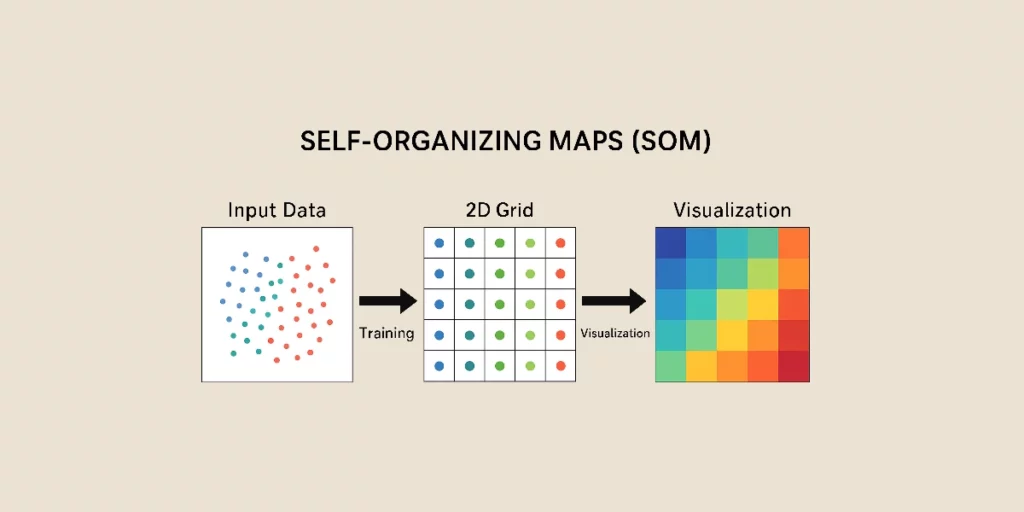
Self-Organizing Maps, oder SOM, sind eine Art von künstlichen neuronalen Netzen (ANN), die für das unüberwachte Lernen genutzt werden. Sie ermöglichen die Reduzierung der Daten-Dimensionalität, während ihre topologische Struktur erhalten bleibt, und sind somit ein mächtiges Werkzeug für das Clustering und die Datenexploration.
Im Gegensatz zu klassischen neuronalen Netzen arbeiten Self-Organizing Maps mit kompetitivem Lernen statt mit Fehlerkorrektur und integrieren eine Nachbarschaftsfunktion, um die räumlichen Beziehungen der Daten zu bewahren.
Ursprung der SOM
Die Self-Organizing Maps wurden in den 1980er Jahren von dem finnischen Forscher Teuvo Kohonen eingeführt. Daher werden sie auch als Kohonen-Karten oder Kohonen Maps bezeichnet.
Inspiriert von den biologischen Mechanismen des Gehirns, ahmen sie die Art und Weise nach, wie Neuronen Informationen organisieren und klassifizieren, um bedeutungsvolle Strukturen zu bilden.
Funktionsweise der SOM
Das Lernen eines Self-Organizing Maps basiert auf einem mehrstufigen Prozess, der es ermöglicht, komplexe Daten in eine organisierte und lesbare Darstellung zu transformieren. Hier ist eine typische Funktionsweise, detailliert Schritt für Schritt, eines SOM beschrieben.
1. Initialisierung der Gewichte
Bevor das Training beginnt, ist jedem Neuron der Karte ein Gewichtungsvektor zugeordnet, der zufällig initialisiert wird. Dieser Vektor hat die gleiche Dimension wie die Eingabedaten und repräsentiert die Identität jedes Neurons, bevor es durch das Lernen angepasst wird.
2. Auswahl eines Eingabe-Beispiels
In jeder Iteration wird ein Eingabevektor zufällig aus dem Trainings-Dataset ausgewählt. Dieser Vektor repräsentiert einen Datenpunkt, den das SOM auf der Karte organisieren lernen muss.
3. Identifizierung der Best Matching Unit
Sobald das Beispiel ausgewählt wurde, sucht der Algorithmus das Neuron, dessen Gewichte diesem Eingabevektor am nächsten kommen. Diese Nähe wird mittels der euklidischen Distanz oder euklidischen Norm zwischen dem Eingabevektor und den Neuronen gemessen. Das nächstgelegene Neuron wird als BMU (Best Matching Unit) identifiziert.

4. Aktualisierung der Gewichte des BMU und seiner Nachbarn
Nachdem das BMU gefunden wurde, passt der Algorithmus dessen Gewichte an, um sie an den Eingabevektor anzunähern. Auch seine benachbarten Neuronen werden, wenn auch in geringerem Maße, aktualisiert.
Das Ausmaß dieser Aktualisierung hängt von zwei Hauptfaktoren ab:
- Die Lernrate (α oder Alpha): Alpha steuert die Geschwindigkeit, mit der die Gewichte der Neuronen angepasst werden. Sie verringert sich im Laufe der Iterationen, um zu vermeiden, dass sich die Änderungen zu abrupt vollziehen.
- Die Nachbarschaftsfunktion: Die Aktualisierung betrifft die Neuronen um das BMU herum, und ihr Ausmaß nimmt mit der Entfernung ab. Eine übliche Funktion ist die gaußsche Funktion.
Diese Phase ermöglicht es dem BMU und seinen Nachbarn, sich schrittweise an die Eigenschaften der Daten anzunähern, während die topologische Struktur der Beziehungen zwischen den Datenpunkten erhalten bleibt.
5. Reduzierung der Lernrate und der Nachbarschaft
Mit jeder Iteration nehmen die Lernrate und die Größe der Nachbarschaft ab. Dies ermöglicht eine feine Anpassung der Gewichte in den letzten Phasen des Trainings und stellt sicher, dass die Daten gut auf der Karte organisiert sind.
- Zu Beginn ist die Nachbarschaft groß, sodass sich die gesamte Karte global organisieren kann.
- Allmählich wird die Nachbarschaft enger, wodurch die Karte verfeinert und die gebildeten Cluster stabilisiert werden.
6. Konvergenz und Stabilisierung
7. Inferenz und Visualisierung der Ergebnisse
Sobald das SOM trainiert ist, kann es verwendet werden, um neue Daten zu organisieren und die visuelle Analyse zu erleichtern. Die Entfernung zwischen einem Eingabevektor und den Gewichten der Neuronen hilft zu bestimmen, wo sich ein neuer Datenpunkt auf der Karte befindet.
Eine häufige Methode zur Visualisierung der SOM besteht darin, die verschiedenen Bereiche der Karte mit Farben zu versehen. Je dunkler die Farbe, desto höher die Datenkonzentration.
Ähnliche Datencluster erscheinen deutlich auf der Karte, was eine intuitive Visualisierung der Beziehungen zwischen verschiedenen Kategorien bietet.
Vorteile und Nachteile der SOM
Die SOM bieten mehrere bemerkenswerte Vorteile. Sie ermöglichen es, die Dimensionalität der Daten zu reduzieren, während deren topologische Organisation erhalten bleibt. Dank ihrer intuitiven grafischen Darstellung erleichtern sie die Visualisierung und Interpretation komplexer Datensätze. Sie werden häufig für das Clustering verwendet, selbst ohne Kenntnis der in den Daten vorhandenen Klassen.
Jedoch haben die SOM auch einige Einschränkungen. Sie passen sich schlecht an rein kategoriale oder gemischte Daten an (außer nach geeigneter Kodierung), die keiner Logik im Darstellungsraum folgen. Ihre Trainingszeit kann lang sein und ihre Leistung hängt von der richtigen Einstellung der Parameter ab.
Anwendungen der SOM
Die SOM werden in verschiedenen Bereichen verwendet, um Daten zu organisieren und zu analysieren. Zum Beispiel im Marketing-Bereich, wo sie Kunden nach ihrem Kaufverhalten gruppieren, um die Geschäftsstrategien zu optimieren.
In der Dimensionsreduktion erleichtern sie das Mapping hochdimensionaler Daten. Dadurch wird ein besseres Verständnis der internen Beziehungen der Daten ermöglicht.
In der Anomalieerkennung werden sie verwendet, um betrügerische Transaktionen zu identifizieren, indem Datenpunkte herausgefiltert werden, die keinem vordefinierten Cluster entsprechen.
Zur Datenvisualisierung helfen sie dabei, die Populationen und die Beziehungen zwischen verschiedenen Parametern besser zu verstehen. Indem sie einen komplexen Datensatz in eine 2D-Darstellung umwandeln, ermöglichen sie es, schnell Trends und unsichtbare Muster in rohen Tabellen zu erkennen.

Fazit
Die SOM sind ein leistungsstarkes Werkzeug für unüberwachte Lernprozesse in der Cluster-Analyse, der Dimensionalitätsreduktion und der Datenvisualisierung. Sie haben Einschränkungen im Hinblick auf Trainingszeit und Anpassung an gemischte Daten. Sie finden Anwendung in der Finanzbranche, im Marketing, im Gesundheitswesen und in der Bildanalyse. Ihre Fähigkeit, verborgene Strukturen in den Daten aufzudecken, macht sie zu einer unverzichtbaren Wahl für die Exploration nicht etikettierter Daten.