Hier findest Du unseren vierten Artikel über Deep Learning. Lies die ersten Artikel, um Deine Kenntnisse über Deep Learning, Machine Learning und Künstlicher Intelligenz sowie über die Funktionsweise und Anwendungen von neuronalen Netzwerken aufzufrischen. Lies auch noch einmal den Artikel über das CNN: Convolutional Neural Network. Und jetzt los mit unserem heutigen Thema !
Inhaltsverzeichnis:
Nun wirst Du im Detail erfahren, wie künstliche neuronale Netze lernen und wie sie sich in einem Netz artikulieren.
Neuronale Netze - eine kurze Auffrischung
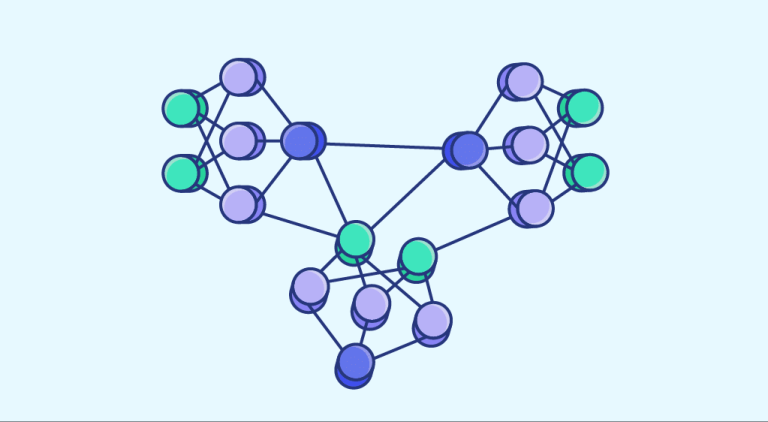
Multilayer perceptron (mehrlagiges Perzeptron) ist ein Stapel von Perzeptronen, die in eine Schicht gelegt werden. Nehmen wir das folgende Beispiel, um das Konzept zu veranschaulichen:
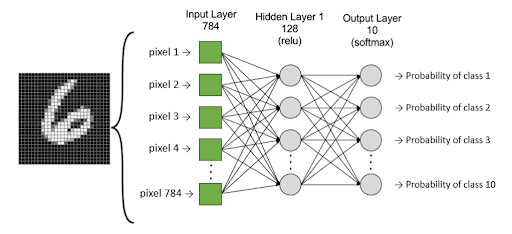
Das Modell besteht aus der Klassifizierung (in 10 Klassen) von Bildern handgeschriebener Zahlen. Die grünen Quadrate sind die Eingabeschicht unseres Modells, d. h. die Werte der Pixel. Die mittlere und die Ausgabeschicht sind Perzeptrons, die durch graue runde Kreise dargestellt werden. Die letzte Schicht hat 10 Neuronen, da es 10 Klassen gibt, und gibt die entsprechende Wahrscheinlichkeit für jede Klasse zurück.
Wir können das Modell sehr einfach in Tensorflow implementieren:
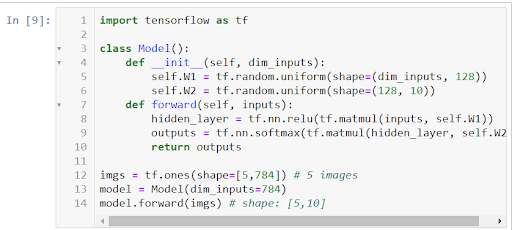
Trainieren des Modells
Um unser Modell zu trainieren, d.h. die passenden Gewichte zu finden, müssen wir eine Funktion definieren, die den Fehler unseres Modells quantifiziert. Normalerweise verwenden wir bei Klassifikationsproblemen die Funktion „cross-entropy“, um den Fehler zu messen.
Unser Optimierungsproblem besteht darin, die Gewichte unseres Modells zu finden, die unsere Fehlerfunktion minimieren:
J(w)Mit Deep Learning sind wir mit komplexen Minimierungsproblemen konfrontiert, für die es keine explizite Lösung gibt. Daher werden Optimierungsmethoden wie der Gradientenabstieg verwendet, um sie zu lösen.
Gradientenabstieg: Um abzusteigen, muss man nach unten gehen
Um das Konzept des Gradientenabstiegs auf intuitive Weise kennenzulernen, kannst Du unser Video zu diesem Thema schauen:
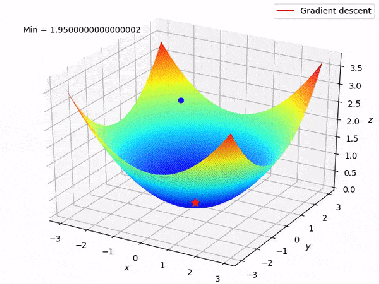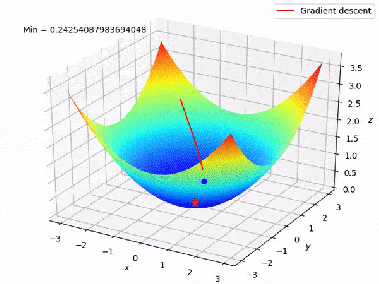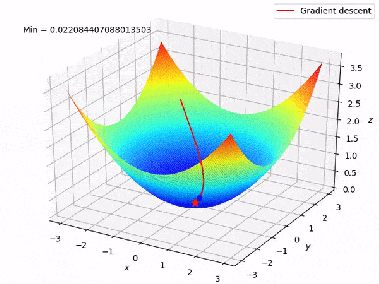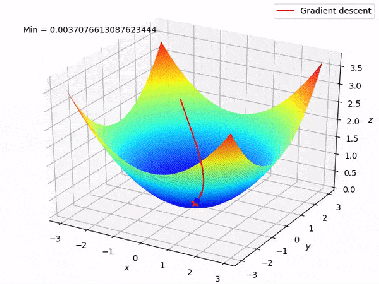
In unserem obigen Beispiel kann man sich die Verlustfunktion (Fehlerfunktion) als einen Berg vorstellen. Die Koordinaten (Modellgewichte) des Punktes mit der geringsten Höhe werden gesucht. Der Wert des Gradienten der Verlustfunktion entspricht der Richtung und Winkel des Hangs des Berges an einem bestimmten Punkt:
- Wenn die Norm des Gradienten hoch ist, ist der Hang sehr steil.
- Wenn die Norm des Gradienten niedrig ist, ist der Hang nur wenig geneigt.
- Wenn die Gradientennorm null ist, befindet man sich auf einer flachen Ebene (Minimum).
Daher besteht der Gradientenabstieg anfänglich darin, die Gewichte zufällig zu wählen und die Inverse des Gradienten bei jeder Iteration zu verfolgen:
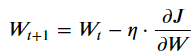
Mit:
- Wt: die Parameter unseres Modells
- η: Schrittweite des Gradienten, d. h. die Lernrate.
- J: Verlustfunktion
Mit einer zu großem oder zu kleinem Schrittweite wird der MLP-Algorithmus zu keiner zufriedenstellenden Lösung konvergieren. Die richtige Schrittweise zu finden, ist die ganze Herausforderung des Deep Learning.
Zusammenfassend kann man sagen, dass sich das künstliche Neuron, auch Perzeptron genannt, wie ein lineares Klassifikationsmodell verhält. Das mehrschichtige Perzeptron hingegen verbindet und stapelt Perzeptrons in Form von Schichten, um die Komplexität der Regelerstellung zu erhöhen.
Nachdem wir die Parameter des Modells definiert haben, haben wir gesehen, dass es notwendig ist, den Fehler des Modells zu quantifizieren. Um dies zu erreichen, verwendet Deep Learning hauptsächlich Gradientenabstieg, um die Gewichte so anzupassen, dass die Verlustfunktion minimiert wird.
Um die Mathematik hinter diesem Gradientenabstiegsalgorithmus und die Bedeutung der Lernrate zu erforschen, kannst Du diesen Artikel lesen.
Im Folgenden stellen wir Dir Transfer Learning vor, eine erfolgreiche Lernkategorie, die in Deep Learning verwendet wird und sich stark am menschlichen Lernen zu orientieren scheint!
- Artikel: Deep Learning oder Tiefes Lernen: Was ist das denn?
- Artikel: Convolutional Neural Network
- Artikel: Transfert Learning