Der Slogan von Cambridge Analytica „Data drives all we do“ wird immer wieder bestätigt: Daten beeinflussen und strukturieren unsere Entscheidungen als Verbraucher, Bürger, Politiker, Unternehmer…
Diese Daten sind eine Fülle an Informationen für die Entscheidungsfindung.
Im kleinen Maßstab ist das relativ einfach. Aber Datenexperten brauchen leistungsfähige Werkzeuge, um die Gesamtheit der Informationen auf Makroebene (wie auf der Ebene der französischen Bevölkerung) zu verarbeiten und zu sortieren.
Spectral Clustering ist genau eines dieser Werkzeuge.
Was ist also Spectral Clustering und wozu dient es? Was sind die Vorteile und Grenzen dieses Modells?
Was ist Spectral Clustering?
Definition
Spectral Clustering ist eine der Komponenten des maschinellen Lernens und der künstlichen Intelligenz.
Es handelt sich dabei um einen Algorithmus zur Partitionierung von Daten, der auf der Spektralgraphentheorie und der linearen Algebra basiert.
Die Idee dahinter ist, einen Graphen in mehrere kleine Gruppen mit ähnlichen oder nahen Werten zu segmentieren.
Der Unterschied zwischen Clustering und Klassifizierung
Bei der Klassifizierung werden die Daten nach einer vorher festgelegten Klasse oder Gruppe gruppiert.
Im Gegensatz dazu kennt der Algorithmus beim Clustering die Klassen nicht, bevor er die Gruppierung vornimmt. Dies wird als unüberwachte Lerntechnik bezeichnet.
Die verschiedenen Arten der Datenpartitionierung
Es gibt verschiedene Arten der Datenpartitionierung, die sich in ihrer Funktionsweise und ihrem Zweck unterscheiden. In diesem Zusammenhang ist zwischen spektralem Clustering :
- K-means: Hier geht es darum, einen Referenzdurchschnitt in einem Datensatz zu ermitteln. Die Idee ist es, ein typisches Profil zu definieren, das die meisten Menschen erreichen kann.
- Die spektrale Datenpartitionierung hingegen zielt darauf ab, verschiedene Gruppen mit möglichst vielen Gemeinsamkeiten zu bilden.
- DBSCAN: Dieser Algorithmus basiert auf der Distanz und der Dichte der Cluster, um Untergruppen zu bilden. Das spektrale Clustering hingegen basiert auf der Ähnlichkeit der Daten.
Wozu dient das Spectral Clustering?
Wer verwendet Spectral Clustering?
Spectral Clustering wird besonders von Marketingfachleuten eingesetzt, um das Verhalten von Nutzern oder Zielgruppen zu verstehen.
💡Aber Achtung: Dieser Algorithmus erfordert spezielle Fähigkeiten. Er sollte von Datenanalysten, Datenwissenschaftlern und anderen Datenanalyseexperten verwendet werden.
In welchen Bereichen wird Spektralclustering eingesetzt?
Da die spektrale Partitionierung die Verarbeitung großer Datenmengen ermöglicht, wird diese Methode häufig für Marketingzwecke eingesetzt. Unternehmen nutzen diesen Algorithmus, um ihre Zielgruppen nach ihren Erwartungen, Bedürfnissen, Profilen, Reifegraden usw. zu segmentieren.
Darüber hinaus kann Spectral Clustering auch in der Politik eingesetzt werden, vor allem in Wahlzeiten. Indem die Masse der Wähler in kleine Gruppen aufgeteilt wird, können die Kandidaten mit jedem einzelnen Wähler persönlicher kommunizieren.
Wie funktioniert der Spectral Clustering Algorithmus?
Der Algorithmus für das Spektralclustering besteht aus mehreren Schritten:
- Die Erstellung eines Graphen durch die Affinitätsmatrix (oder Ähnlichkeitsmatrix, Nachbarschaftsmatrix) ;
- Segmentierung der Datenpunkte in kleinere Dimensionsräume ;
- Die Verwendung von Eigenwerten und Eigenvektoren zur Definition von Subgraphen.
Um die Funktionsweise besser zu verstehen, erklären wir dir die drei wichtigsten Begriffe des Spectral Clustering.
Die Grafiken
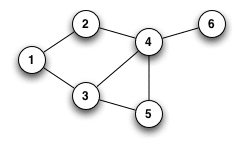
Graphen sind eine Menge von Knoten, die durch eine Menge von Kanten verbunden sind. Diese Knoten und Kanten können miteinander verbunden sein oder nicht.
Aber in jedem Fall können mit Graphen viele verschiedene Datentypen dargestellt werden.
Für das spektrale Clustering muss man von einem Graphen ausgehen; entweder von einem Nachbarschaftsgraphen, einem Graphen der nächsten Nachbarn (KNN) oder einem vollständig verbundenen Graphen.
Dann wird dieser in die Form einer Matrix übersetzt. Genauer gesagt, die benachbarte Matrix.
Die Matrizen
Die angrenzende Matrix (A) fasst die Beziehungen zwischen allen Datenpunkten des Graphen zusammen.
Beispiel:
Daten, die interagieren = 1
Daten, die nicht interagieren = 0.
Die Matrix kann dann wie in der folgenden Tabelle aussehen:
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 |
Danach kommt die Gradmatrix (D) zum Einsatz. Basierend auf der Matrix A berechnet sie die Summe der Verbindungen (horizontal und vertikal). Auf der Grundlage des vorherigen Beispiels sieht das Ergebnis wie folgt aus:
| 0 | 0 | 0 | 2 |
| 0 | 3 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 |
Die Laplacesche Matrix (L) schließlich entspricht der Matrix mit dem Grad minus der benachbarten Matrix, also L=D-A.
| -1 | 0 | 0 | -1 |
| 0 | 2 | -1 | -1 |
| 0 | -1 | 1 | 0 |
| 1 | -1 | 0 | 0 |
Diese Matrix wird dann visuell in Form eines Graphen dargestellt, der als Laplacian-Graph bezeichnet wird.
Die Vektoren
Die visuelle Darstellung des Laplacian-Graphen (A) setzt voraus, dass man die Eigenwerte (eigenvalues= λ) und die Eigenvektoren (eigenvectors=x) kennt.
Sei Ax = λx.
Es ist möglich, die Eigenwerte und Eigenvektoren einer Matrix mithilfe von numpy in Python zu finden.
Die Verwendung dieser Matrizen und Vektoren ermöglicht es dann, mehrere Subgraphen auf der Grundlage ihrer Ähnlichkeiten zu gruppieren. Eine der gängigsten Methoden für das Spectral Clustering ist die Anwendung eines klassischen Clustering-Algorithmus wie der Kmean-Methode auf die Eigenvektoren dieser Matrix. Diese Methode kann direkt mit dem Spectral Clustering-Modul der Sklearn-Bibliothek implementiert werden.
Die Eigenwerte werden verwendet, um die optimale Anzahl von Clustern für die Partitionierung deiner Daten zu bestimmen.
Gut zu wissen: Die Anzahl der Untergrafiken (Cluster) hängt vom Ziel und dem gewünschten Grad der Zielgruppenansprache ab. Aus Makrosicht ist es besser, eine geringe Anzahl von Clustern zu haben, um einen besseren Überblick zu erhalten. Aus einer Mikroperspektive ist es jedoch ebenso interessant, mit möglichst vielen Untergruppen ins Detail zu gehen.
Warum sollte man die spektrale Partitionierung verwenden?
Die Verwendung der spektralen Partitionierung ist absolut unerlässlich, um deine Zielgruppe zu verstehen und sie auf personalisierte Weise anzusprechen.
Nehmen wir als Beispiel Personen, die ein Abonnement für eine Bekleidungsmarke haben (das ist die Basis unserer angrenzenden Matrix). Nur weil sie alle die gleiche Affinität aufweisen, heißt das nicht, dass sie alle das gleiche Profil haben.
Unter den Abonnenten können sich befinden:
- Treue Kunden ;
- Interessenten, die zögern;
- Stylisten, die nach Inspirationen suchen;
- Marketingexperten, die ihre Arbeit beobachten;
- Und so weiter.
Mithilfe von Spectral Clustering können die Daten in kleinere Untergruppen mit geringeren Abmessungen segmentiert werden.
Für Unternehmen bedeutet die Kenntnis jeder Untergruppe, dass sie ihre Kommunikation und ihr Angebot anpassen können
Es geht darum, die richtigen Leute zur richtigen Zeit und auf die richtige Art und Weise anzusprechen, um die Chancen auf eine Konversion zu erhöhen.
Und wie bereits erwähnt, können auch Politiker diesen Algorithmus nutzen, um ihre Wähler zu überzeugen.
Was sind die Vor- und Nachteile von Spectral Clustering?
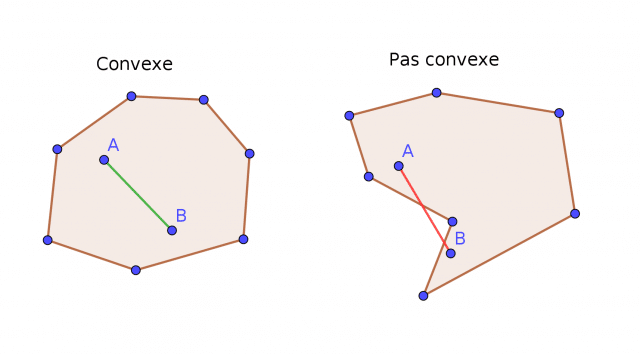
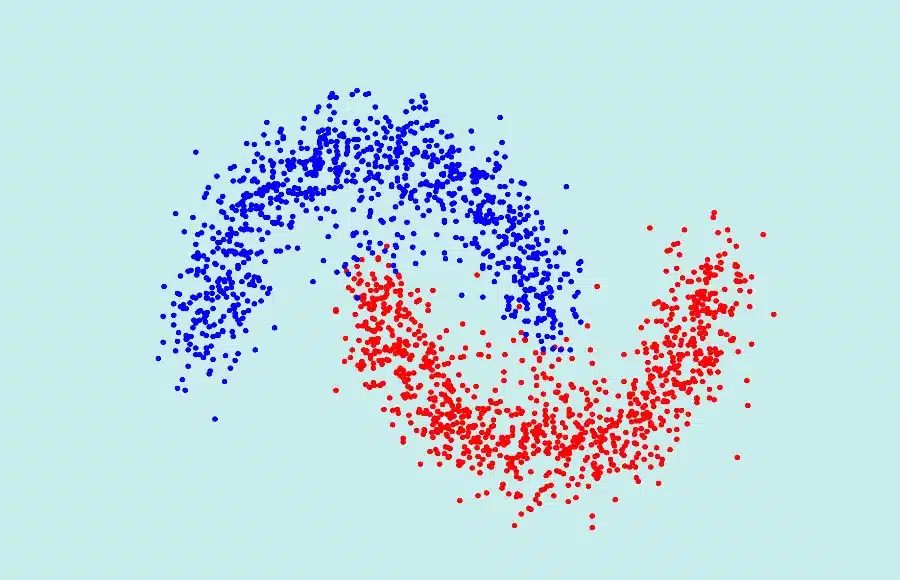
Der unbestreitbare Vorteil von Spectral Clustering ist seine Fähigkeit, einen Satz von Daten, die nicht konvex zueinander sind, zu klassifizieren.
Es handelt sich jedoch um ein komplexes Konzept, das nicht nur ein gutes Verständnis seiner Funktionsweise erfordert, sondern auch und vor allem die Beherrschung der linearen Algebra und der spektralen Graphentheorie.
Das Python-Tool numpy kann die Berechnungen durchführen, um die Arbeit der Analysten zu vereinfachen.
Wie kann man sich in Spektralclustering ausbilden lassen?
Da das Spectral Clustering besonders komplex ist, ist es wichtig, seine Funktionsweise wirklich im Detal zu verstehen.
In diesem Zusammenhang wird dir eine exzellente Fortbildung in Data Science ermöglichen, die notwendigen Werkzeuge zu beherrschen, um diesen Algorithmus zu implementieren.
Du kannst diese Fähigkeiten dann in Unternehmen oder öffentlichen Einrichtungen einsetzen, um ihnen zu helfen, ihre Kommunikation, ihre Angebote und ihre Leistungen zu verbessern.