Willkommen zum zweiten Teil dieses Dossiers über die Support Vector Machine.
Im vorherigen Artikel haben wir die Funktionsweise und die Hauptfehler von Maximal Margin Classifier beschrieben.
Unser Ziel ist es nun, unserem Algorithmus zu erlauben, eine gewisse Anzahl von Fehlern bei der Auswahl der Trennungsgeraden zu machen. Dies wird als „soft margin“ bezeichnet, was man mit „weicher Rand“ übersetzen könnte. Wir werden nun die Funktionsweise des Soft Margin Classifiers-Algorithmus, der zwischen der Support Vector Machine und dem Maximal Margin Classifier angesiedelt ist, im Detail erläutern.
Soft Margin Classifiers
Im letzten Artikel haben wir den Begriff „Rand“ definiert, d. h. den Abstand zwischen einer Geraden und der nächstgelegenen Beobachtung.
In diesem zweiten Teil verwenden wir den Begriff „Rand“ auch, aber er bezieht sich auf die Menge der Punkte, die näher an der Geraden liegen als die nächstgelegene Beobachtung.
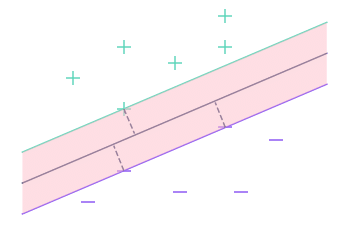
Hier zum Beispiel ist der Rand die rosafarbene Fläche in der Grafik. Es handelt sich dabei um den Raum zwischen den beiden äußeren Geraden.
Um unseren Algorithmus flexibler zu gestalten, werden wir einen Schwellenwert verwenden, der die Anzahl der Beobachtungen angibt, die wir innerhalb des Spielraums tolerieren. Dann versuchen wir, wie zuvor, die Trennungsgerade zu bestimmen, die den Spielraum maximiert. Dabei wird jedoch nicht mehr darauf geachtet, welche Beobachtungen sich innerhalb des Spielraums befinden. Dies ermöglicht es uns, eine gewisse Unempfindlichkeit gegenüber Extremwerten zu erreichen.
Folgendes erhalten wir im vorherigen Beispiel mit unterschiedlichen Schwellenwerten:



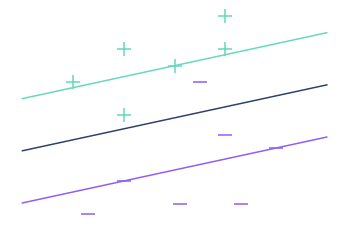
Wie zu erwarten war, erhöht eine Erhöhung des Schwellenwerts die Gewinnspanne.
Dies bedeutet jedoch nicht, dass die Klassifizierung besser ist. Wir verwenden daher die Kreuzvalidierung, um den bestmöglichen Schwellenwert zu wählen.
Wenn du noch nie etwas von Kreuzvalidierung gehört hast, hier eine kurze Definition.
Wenn du den Schwellenwert erhöhst, verringerst du die Varianz, erhöhst aber die Verzerrung. Im Fachjargon heißt es: Je höher der Schwellenwert, desto geringer das Risiko des Overfittings.
Hinweis: Die Beobachtungen, die sich innerhalb und an den Grenzen des Randes befinden, werden Support Vectors genannt, und der Soft Margin Classifiers-Algorithmus heißt auch Support Vectors Classifier.
SVM - Support Vector Machine
Wir haben eine Lösung für das erste Problem gefunden, aber nicht für das zweite. So funktioniert der SVM oder Support Vector Classifier Algorithmus immer noch nicht in folgendem Fall:

Wenn der Algorithmus nicht funktioniert, sagt man, dass die Daten nicht linear trennbar sind, und es gibt mathematische Werkzeuge, um zu bestimmen, ob ein Datensatz linear trennbar ist oder nicht.
Wenn man also mit einem Datensatz konfrontiert wird, verwendet man diese Werkzeuge. Wenn der Datensatz linear trennbar ist, muss man nicht lange suchen, sondern wendet den Soft Margin Classifier an. Schwieriger wird es, wenn der Datensatz nicht linear trennbar ist.
Um die Visualisierung zu vereinfachen, ändern wir den Datensatz und nehmen diesmal Beobachtungen der Dimension 1, d.h. auf einer Geraden (und nicht auf einer Ebene).

Es ist also klar, warum in dieser speziellen Konfiguration keine Gerade die „+“ und „-“ trennen kann.
Die Idee der Support Vector Machine ist es, die Daten in einen größeren Raum zu projizieren, um sie so trennbar zu machen.
Nehmen wir unser Beispiel in Dimension 1 wieder auf und projizieren die Daten in einen Raum der Dimension 2. Dazu benötigen wir eine sogenannte Kernelfunktion (oder kernel function). Diese Funktion dient als Vermittler zwischen den beiden Räumen.
Nehmen wir zum Beispiel die Würfelfunktion (f(x) = x^3) als Kernfunktion. So wendest du die Kernfunktion auf den Datensatz an, um ihn in einen Raum der Dimension 2 zu projizieren:
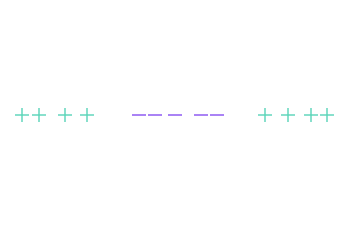
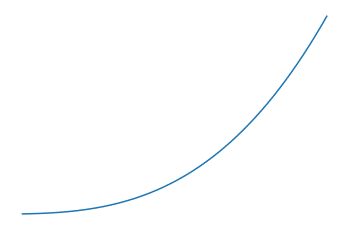

Anders ausgedrückt: Wenn wir die Kernfunktion mit f bezeichnen, setzen wir für jede Beobachtung x einen Punkt mit den Koordinaten (x, f(x)) in die Ebene.
Der projizierte Datensatz ist nun trennbar, wie das nächste Bild zeigt. Wir können den Soft Margin Classifiers-Algorithmus, dessen Funktionsweise wir zuvor erklärt haben, verwenden, um die beste Trennungsgerade zu berechnen, und das war’s dann.
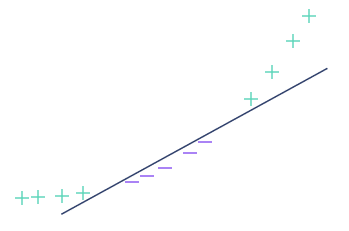
Wir haben gerade die Funktionsweise der Support Vector Machine detailliert beschrieben. Auch wenn wir absichtlich einige Details nicht erwähnt haben (z. B. die Wahl der Kernfunktion), hast du jetzt einen Überblick über das Thema.
SVM-Algorithmen können für Klassifikationsprobleme mit mehr als zwei Klassen und für Regressionsprobleme angepasst werden. Es handelt sich also um eine einfache und schnelle Methode, die auf alle Arten von Datenbeständen angewendet werden kann, was sicherlich ein Grund für ihren Erfolg ist. Wo ein neuronales Netz eine Vorarbeit erfordert, um die richtige Struktur und die richtigen zu verwendenden Parameter zu bestimmen, erzielen SVMs auch ohne Vorbereitung gute Ergebnisse. Wenn du mehr über Machine Learning erfahren möchtest, lade ich dich ein, dir einen anderen Artikel anzusehen, der die Funktionsweise von Boosting-Algorithmen detailliert beschreibt.