Qu'est ce qu'une probabilité ?
Une probabilité quantifie la chance/le risque que se produise un évènement. Cette valeur est toujours comprise entre 0 et 1.
Quelques cas d'usage de la probabilité du quotidien
Le lancer d'un dé
Lorsqu’on lance un dé non pipé à 6 faces, on a 1 chance sur 6 d’obtenir un 3.
On définit l’événement A : « On obtient un 3 », et on note \mathbb{P}(A) la probabilité de cet évènement dont la valeur est : \mathbb{P}(A) = \frac{1}{6} On peut définir d’autres évènements comme :
- B: « Le nombre obtenu est impair »
- C: « Le nombre est supérieur ou égal à 5 »
On a alors : \mathbb{P}(B) = \frac{3}{6} = \frac{1}{2} \mathbb{P}(C) = \frac{2}{6} = \frac{1}{3}
On peut aussi calculer la probabilité que 2 évènements se produisent en même temps.
- B \cap C: « Le nombre obtenu est impair » ET « Le nombre obtenu est supérieur ou égal à 5 ».
Donc B \cap C est l’événement « On obtient un 5 ».
La probabilité qu’il se produise est : \mathbb{P}(B \cap C) = \frac{1}{6}
De même, on peut calculer la probabilité qu’au moins un événement se produise parmi plusieurs.
L’événement D = B \cup C correspond à « Le nombre obtenu est impair » OU « Le nombre obtenu est supérieur ou égal à 5 », c’est-à-dire « Le nombre obtenu est 1, 3, 5, ou 6 ».
Dans ce cas : \begin{aligned} \mathbb{P}(D) &= \mathbb{P}(B \cup C) \\ &= \mathbb{P}(B) + \mathbb{P}(C) – \mathbb{P}(B \cap C) \\&= \frac{1}{2} + \frac{1}{3} – \frac{1}{6} \\\mathbb{P}(D) &= \frac{2}{3} \\\end{aligned}
Un paquet de cartes
Un paquet de cartes classique est composé de 52 cartes avec :
- 4 couleurs (pique, carreau, trèfle, coeur)
- 13 cartes par couleur (du 2 au 10, valet, dame, roi, as)
On s’intéresse au résultat lorsqu’on tire une seule carte du paquet.
On définit les évènements :
- C : « La carte est un cœur »
- T : « La carte est une tête (valet, dame ou roi) »
- A : « La carte est un as »
Alors :
- \mathbb{P}(C) = \frac{13}{52} = \frac{1}{4}
- \mathbb{P}(T) = \frac{12}{52} = \frac{3}{13}
- \mathbb{P}(A) = \frac{4}{52} = \frac{1}{13}
On a aussi :
- \mathbb{P}(T \cap C) = \frac{3}{52}
- \mathbb{P}(T \cap A) = 0
- \mathbb{P}(A \cap C) = \frac{1}{52}
Le complémentaire de ces évènements est :
- C^C : « La carte n’est pas un cœur »
- T^C : « La carte n’est pas une tête »
- A^C : « La carte n’est pas un as »
Dans ce cas, on a :
- \mathbb{P}(C^C) = 1 – \mathbb{P}(C) = 1 – \frac{1}{4} = \frac{3}{4}
- \mathbb{P}(T^C) = 1 – \mathbb{P}(T) = 1 – \frac{3}{13} = \frac{10}{13}
- \mathbb{P}(A^C) = 1 – \mathbb{P}(A) = 1 – \frac{1}{13} = \frac{12}{13}
Si on tire une carte et qu’on sait que c’est un cœur, alors la probabilité que la carte soit une tête vaut \frac{3}{13}.
On parle alors de probabilité conditionnelle : il s’agit de la probabilité conditionnellement à une information donnée.
On écrit : \mathbb{P}(T | C) = \frac{\mathbb{P}(T \cap C)}{\mathbb{P}(C)}/
On sait que la carte est un cœur. Il y a au total 13 cartes cœur, dont 3 sont des têtes, on a donc une probabilité de \frac{3}{13} d’avoir tiré une tête en sachant que c’est un cœur.
Par le calcul :
\begin{aligned} \mathbb{P}(T | C) & = \frac{\mathbb{P}(T \cap C)}{\mathbb{P}(C)} \\ & = \frac{\frac{3}{52}}{\frac{1}{4}} \\ & = \frac{3}{13} \end{aligned}
À votre tour
On utilise un paquet de 52 cartes.
- Quelle est la probabilité de ne pas tirer un 8 ?
- Quelle est la probabilité de tirer un as ou un pique ?
- Quelle est la probabilité de tirer un roi, sachant que la carte tirée n’est pas un trèfle ?
Vocabulaire et premières propriété
Espace de probabilité
On se place sur un espace probabilisé (\Omega, \mathcal{A}, \mathbb{P}) où :
- \Omega est l’univers
- \mathcal{A} est une tribu sur \Omega. C’est l’ensemble des évènements sur \Omega
- \mathbb{P} est une mesure de probabilité sur (\Omega,\mathcal{A})
Quelques propriétés
Soient A et B deux évènements :
- \mathbb{P}(\emptyset)=0 et \mathbb{P}(\Omega)=1
- \mathbb{P}(A^C)= 1 – \mathbb{P}(A)
- \mathbb{P}(A \cup B)=\mathbb{P}(A) + \mathbb{P}(B) -\mathbb{P}(A \cap B)
Pour comprendre cette dernière égalité :
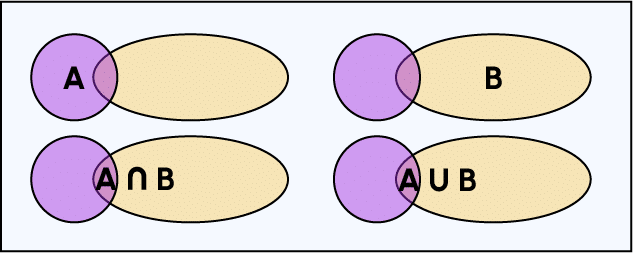
En calculant la probabilité de l’union de deux ensembles, on retire une partie qu’on pourrait compter deux fois : l’intersection A\cap B, car A\cap B est inclus dans A et est inclus aussi dans B.
Système complet d'événements
On appelle système complet d’évènements \left(E_i\right)_{i \in I} un ensemble de parties de \Omega, avec I fini ou dénombrable vérifiant :
- \bigcup\limits_{i \in I} E_i = \Omega
- \forall \left(i,j\right) \in I^2, \quad i \ne j \Rightarrow E_i \cap E_j = \emptyset
Formule des probabilités totales
On considère un système complet d’évènements \left(E_i\right)_{i \in I}.
Alors pour tout évènement A, on a : \begin{aligned} \mathbb{P}\left(A\right) &= \sum \limits_{i \in I}{} \mathbb{P}\left(A \cap E_i\right) \\ &= \sum \limits_{i \in I}{} \mathbb{P}\left(A \vert E_i\right)\mathbb{P}\left(E_i\right) \\ \end{aligned}
Conditionnement
On considère un espace probabilisé \left(\Omega, \mathcal{A}, \mathbb{P}\right).
Probabilité conditionnelle
Soit A \in \mathcal{A} un évènement tel que \mathbb{P}\left(A\right) \ne 0
On appelle probabilité conditionnelle sachant A et on la note \mathbb{P}\left(\cdot\vert A \right) l’application définie sur \mathcal{A} par
\forall B \in \mathcal{A} \quad \mathbb{P}\left(B \vert A\right) = \frac{\mathbb{P}\left(B \cap A\right)}{\mathbb{P}\left(A\right)}
Théorème de Bayes
On considère deux évènements A et B tels que \mathbb{P}\left(B\right) \ne 0.
Alors \mathbb{P}\left(A \vert B\right) = \frac{\mathbb{P}\left(B \vert A\right) \mathbb{P}\left(A\right)}{\mathbb{P}\left(B\right)}
Exemple
Dans une population, une maladie affecte 3 personnes sur 100.
Lors du dépistage de cette maladie, il est possible que le test donne un résultat incorrect :
- Lorsqu’une personne est malade, il y a 2\% de risques que le test soit négatif
- Si une personne n’est pas malade, il y a 0,5\% de risques que le test soit positif.
Question
Quelle est la probabilité qu’une personne dont le test est positif soit effectivement malade ?
Réponse
Notons les évènements :
- M : L’individu est malade
- T : Le résultat du test est positif
Alors on connaît les probabilités suivantes :
- \mathbb{P}\left(M\right) = \frac{3}{100} (c’est la probabilité qu’un individu soit malade)
- \mathbb{P}\left(T^C | M\right) = \frac{2}{100} (c’est la probabilité que le test d’une personne malade soit négatif)
- \mathbb{P}\left(T | M^C\right) = \frac{5}{1000} (c’est la probabilité que le test d’une personne saine soit positif)
Il s’agit de calculer la probabilité \mathbb{P}\left(M | T\right)
Calculons \mathbb{P}\left(M | T\right)
\begin{aligned} \mathbb{P}\left(M | T\right) &= \frac{\mathbb{P}\left(M\cap T\right)}{\mathbb{P}\left(T\right)} \\ &= \frac{\mathbb{P}\left(T|M\right)\mathbb{P}\left(M\right)}{\mathbb{P}\left(T\right)} \\ &= \frac{\left(1 – \mathbb{P}\left(T^C|M\right)\right)\mathbb{P}\left(M\right)}{\mathbb{P}\left(T\right)}\end{aligned}
Le problème est qu’on ne connaît pas \mathbb{P}\left(T\right). Pour calculer cette valeur, il est possible d’utiliser la formule des probabilités totales. Alors les évènements T\cap M et T \cap M^C forment un système complet d’événements dans T. La formule des probabilités totales donne :
\begin{aligned}\mathbb{P}\left(T\right) &= \mathbb{P}\left(T\cap M\right) + \mathbb{P}\left(T\cap M^C\right) \\ &= \mathbb{P}\left(T|M\right)\mathbb{P}\left(M\right) + \mathbb{P}\left(T|M^C\right)\mathbb{P}\left(M^C\right) \\ &= \left(1 – \mathbb{P}\left(T^C|M\right)\right)\mathbb{P}\left(M\right) + \mathbb{P}\left(T|M^C\right)\left(1 – \mathbb{P}\left(M\right)\right)\end{aligned}
A présent, nous pouvons calculer \mathbb{P}\left(M | T\right), puisque toutes les valeurs impliquées sont connues. \begin{aligned} \mathbb{P}\left(M | T\right) &= \frac{\left(1 – \mathbb{P}\left(T^C|M\right)\right)\mathbb{P}\left(M\right)}{\left(1 – \mathbb{P}\left(T^C|M\right)\right)\mathbb{P}\left(M\right) + \mathbb{P}\left(T|M^C\right)\left(1 – \mathbb{P}\left(M\right)\right)} \\ \\ &= \frac{\left(1 – \frac{2}{100}\right)\frac{3}{100}}{\left(1 – \frac{2}{100}\right)\frac{3}{100} + \frac{5}{1000}\left(1 – \frac{3}{100}\right)} \\ \\ &= \frac{588}{685} \\ \mathbb{P}\left(M | T\right) & \approx 85,84 \% \end{aligned}
Conclusion
L’objectif de cet article était de donner toutes les bases nécessaires en probabilité pour bien comprendre la partie 2 (qui ne devrait pas trop tarder 😉). Les probabilités sont utilisées de manière extensive dans plusieurs disciplines ainsi que dans beaucoup d’outils de Machine Learning et de Business Intelligence. Les concepts présentés ci-dessus sont des fondamentaux pour bien comprendre le fonctionnement de ces outils avec une meilleure compréhension de certains algorithmes.
Par ailleurs, les probabilités sont très importantes dans les métiers liés à la data et en particuliers pour les Data Scientists et Analystes. DataScientest peut non seulement vous permettre d’étoffer vos bases mais également vous accompagner dans votre montée en compétence à travers ses différents parcours dédiés. N’hésitez pas à visiter le site internet ou à nous contacter directement.










