L'analyse des séries temporelles est une méthodologie cruciale dans de nombreux domaines, tels que la finance, l'économie, la météorologie et la biologie.
Parmi les différentes approches disponibles, le modèle SARIMAX (Seasonal Autoregressive Integrated Moving Average + exogenous variables) se démarque en tant qu’outil puissant pour modéliser et prévoir à la fois les tendances et les variations saisonnières dans les données temporelles tout en intégrant des variables exogènes dans l’analyse afin d’améliorer la précision des prédictions. Dans cet article, nous allons plonger dans les bases du modèle SARIMAX, examiner ses composantes clés et explorer son application pratique.
Le fondement : modèle ARIMA
Pour bien saisir l’essence du modèle SARIMAX, commençons par explorer les bases du modèle ARIMA (Autoregressive Integrated Moving Average). L’ARIMA est une technique statistique puissante pour modéliser et prévoir des séries temporelles. Il repose sur trois composantes clés : l’autorégression (AR), la moyenne mobile (MA) et l’intégration (I).
- L’autorégression (AR) prend en compte les valeurs passées de la série temporelle pour prédire les valeurs actuelles. Elle est caractérisée par un ordre généralement noté p. L’autorégression consiste à effectuer une régression linéaire sur les p dernières valeurs de la série temporelle afin de prédire la valeur actuelle :
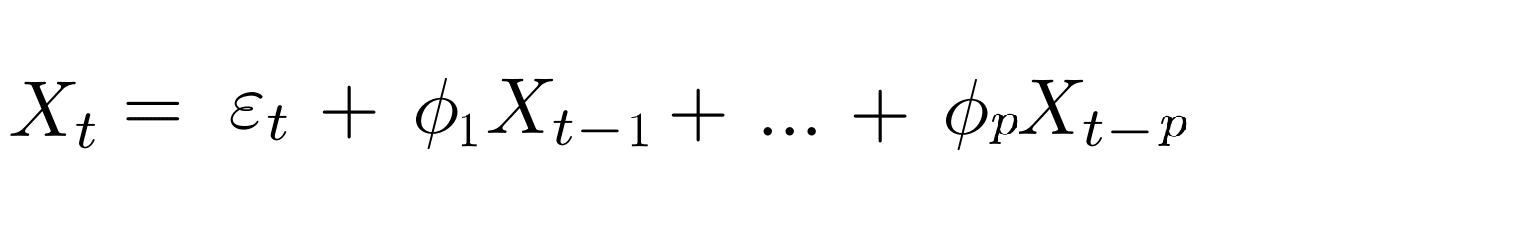
- La moyenne mobile (AM), quant à elle, s’attaque aux erreurs passées dans les prédictions. Elle est caractérisée par un ordre généralement noté q. La moyenne mobile consiste à effectuer une régression linéaire sur les q dernières valeurs des erreurs afin de prédire la valeur actuelle :
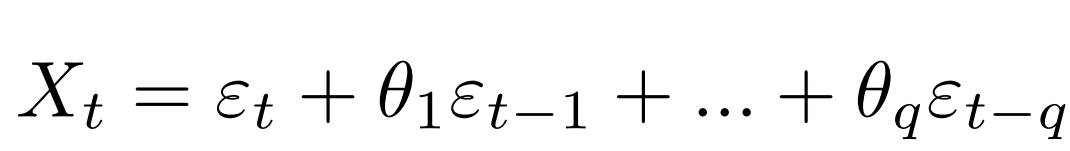
La combinaison de l’autorégression et de la moyenne mobile constitue le modèle ARMA. Ce modèle est efficace sur les séries temporelles stationnaires. Pour appliquer cela sur une série temporelle quelconque, on fait intervenir la composante Intégration (I) du modèle ARIMA.
- L’intégration (I) intervient pour rendre la série temporelle stationnaire, en différenciant les valeurs pour faciliter la modélisation. En effet, la plupart des séries temporelles peuvent être rendues stationnaires après un certain nombre de différenciations.
Le modèle ARIMA se caractérise alors par trois coefficients : son ordre d’autorégression p. Son ordre d’intégration d, qui correspond au nombre de différenciations nécessaires pour rendre la série temporelle stationnaire. Si la série est déjà stationnaire, le coefficient d à choisir serait zéro. Son ordre de moyenne mobile q.
Une fois ces coefficients donnés au modèle ARIMA, celui-ci va s’entraîner sur les données afin de trouver les coefficients de régression optimaux dans l’autorégression et la moyenne mobile pour effectuer des prédictions cohérentes.
Élargissement vers SARIMA : incursion dans les variations saisonnières
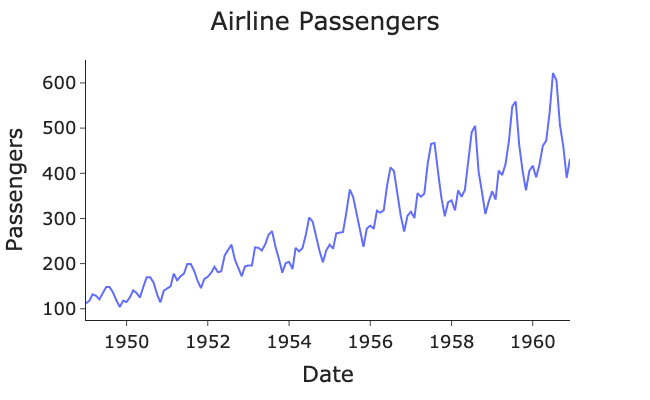
Lorsque les données temporelles exhibent des variations saisonnières, le modèle SARIMA prend la scène. Le terme « Seasonal » est ajouté à ARIMA pour indiquer que ce modèle peut capturer les motifs qui se répètent à intervalles réguliers. Les variations saisonnières peuvent se manifester sur de courtes périodes comme les ventes mensuelles d’une entreprise ou sur de plus longues périodes comme les données climatiques par exemple. En intégrant une composante saisonnière (S), le modèle SARIMA peut modéliser ces schémas récurrents et améliorer les prévisions. Vous pouvez observer un exemple de série temporelle non stationnaire présentant une saisonnalité dans le graphe ci-dessous, qui représente l’évolution du nombre de passagers annuelle d’une compagnie aérienne.
La révolution : SARIMAX et les covariables
Alors que le modèle SARIMA offre déjà une puissante méthode pour modéliser les séries temporelles saisonnières, il peut y avoir des facteurs extérieurs qui influencent ces données. C’est ici que le modèle SARIMAX (Seasonal ARIMA with eXogenous variables) entre en jeu, ouvrant la porte à une analyse encore plus riche.
Les covariables, également appelées variables exogènes, sont des éléments externes qui peuvent influencer la série temporelle étudiée. Dans le contexte des ventes mensuelles d’une entreprise, les covariables pourraient inclure les dépenses publicitaires, les événements spéciaux ou les vacances. Le modèle SARIMAX permet d’intégrer ces covariables dans l’analyse, permettant ainsi de tenir compte des facteurs externes qui peuvent affecter les tendances observées.
Composantes du modèle SARIMAX
Le modèle SARIMAX conserve les composantes clés du modèle SARIMA tout en introduisant deux éléments majeurs : les covariables (X) et la composante des covariables (Z).
- Autorégression (AR) : Comme précédemment, l’autorégression examine les valeurs passées de la série temporelle pour prédire les valeurs actuelles.
- Moyenne Mobile (MA) : La moyenne mobile continue de modéliser les erreurs passées dans les prédictions.
- Intégration (I) : L’intégration est toujours présente pour rendre la série temporelle stationnaire.
- Composante Saisonnière (S) : La composante saisonnière capture les variations qui se répètent à intervalles réguliers.
- Covariables (X) : Les covariables sont des variables extérieures qui peuvent influencer la série temporelle.
- Composante des Covariables (Z) : La composante des covariables permet de modéliser l’effet des covariables sur la série temporelle.
Application pratique de SARIMAX avec covariables
Penchons-nous sur une application concrète du modèle SARIMAX pour mieux appréhender son utilité. Supposons que nous ayons des données mensuelles sur les ventes d’une entreprise ainsi que des données sur les dépenses publicitaires mensuelles en tant que covariables.
- Analyse des données : Avant de construire le modèle, il est crucial d’analyser les tendances, les schémas saisonniers et l’influence potentielle des covariables sur les ventes. C’est l’étape d’exploration de données et de pre-processing.
- Construction du modèle : En choisissant les ordres ARIMA (p, d, q) et la période saisonnière (s), nous ajustons le modèle SARIMAX en tenant compte des covariables (dans ce cas, les dépenses publicitaires).
- Validation et prévisions : Évaluer la performance du modèle en le testant sur une période distincte de celle de l’entraînement. Des métriques telles que l’erreur quadratique moyenne (RMSE) nous donnent un aperçu de la qualité des prédictions. Une fois validé, le modèle est prêt à être utilisé pour des prévisions futures.
Avantages de SARIMAX avec covariables
L’intégration de covariables confère au modèle SARIMAX un avantage significatif. En incorporant des variables exogènes, les prévisions prennent en compte non seulement les tendances internes et saisonnières, mais aussi les facteurs externes qui peuvent influencer la série temporelle. Les décideurs peuvent ainsi prendre des mesures plus informées.

Conclusion
Le modèle SARIMAX représente une avancée significative dans l’analyse des séries temporelles en permettant l’intégration de covariables. En incorporant des variables extérieures pour enrichir l’analyse, ce modèle nous permet de mieux comprendre les tendances et les prédictions futures. Toutefois, comme pour toute méthodologie, il est crucial de maîtriser les paramètres du modèle et de comprendre les résultats pour obtenir des prédictions pertinentes et fiables.
Le modèle SARIMAX avec covariables est une contribution précieuse à la boîte à outils des analystes de séries temporelles, offrant une approche plus complète pour modéliser et prévoir des données influencées par des facteurs externes. Que ce soit pour anticiper les ventes d’une entreprise, prédire les fluctuations des marchés financiers ou comprendre les variations climatiques, le modèle SARIMAX ouvre la voie à des analyses plus précises et à des décisions éclairées.
En exploitant les puissantes capacités d’intégration des covariables de ce modèle, les professionnels peuvent accéder à une perspective plus holistique sur les tendances temporelles et les facteurs qui les sous-tendent. En fin de compte, le modèle SARIMAX propulse l’analyse des séries temporelles vers de nouveaux horizons, renforçant ainsi notre capacité à interpréter et à anticiper les comportements temporels complexes.