Si vous vous êtes déjà intéressé aux séries temporelles, vous avez sûrement dû entendre parler de l’ARIMA ou de l’ARMA. En effet, ce sont les principaux processus utilisés pour modéliser des séries temporelles et ils constituent donc une notion fondamentale lorsque vous débutez dans le domaine.
Si vous ne savez pas encore ce qu’est une série temporelle, je vous conseille vivement d’aller voir notre article sur les séries temporelles que nous avons publié sur le sujet car les notions qui y sont exposées seront ré-utilisées dans cet article.
Le processus ARIMA est une association de différents de processus plus simples que nous allons expliquer dans cet article.
Le processus AR :
Le processus AR signifie autorégressif.
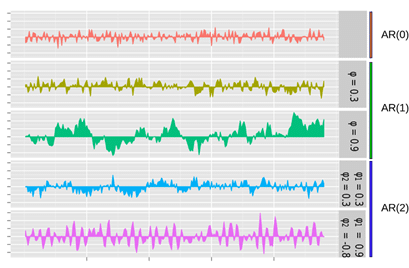
Concrètement, si l’on considère un processus stationnaire Xt, on considère qu’il est autorégressif d’ordre p si l’on peut expliquer sa valeur à l’instant T en utilisant ses p termes précédents.
Mathématiquement, cela signifie que :
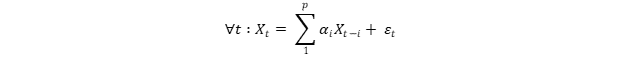
avec ε l’erreur et (𝛼1, …,𝛼p) des réels
Le processus MA :
MA signifie ‘moving average’ ou en français moyenne mobile.
Soit Xt une série temporelle, on considère que c’est un processus MA d’ordre p si on peut exprimer sa valeur à l’instant t comme une combinaison linéaire d’erreur aléatoires (bruit blanc).
Mathématiquement on traduit cela par :
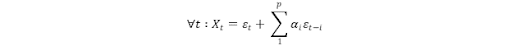
avec ε l’erreur et (𝛼1, …,𝛼p) des réels
Le processus ARMA :
Comme vous vous en doutez, le modèle ARMA est tout simplement une combinaison d’un processus AR et d’un processus MA. Cela permet de modéliser des séries temporelles plus complexes.
Un modèle ARMA d’ordre (p,q) s’écrit donc sous la forme :
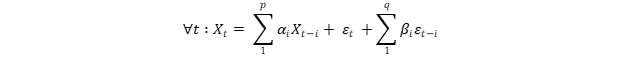
Avec (𝛼1, …,𝛼p) et (𝛽1, …,𝛽q) des réels.
Cependant, l’une des limitations de ce modèle est qu’il ne peut modéliser que des séries temporelles stationnaires.
Ainsi, il ne peut modéliser une série temporelle avec une tendance linéaire croissante. C’est pour pallier ce problème que le modèle ARIMA a été développé
Le modèle ARIMA :
Le I du modèle ARIMA signifie ‘integrated’ pour intégration. En différenciant les séries temporelles, il est possible de retirer les tendances qu’elles présentent pour les stationnariser.
Prenons l’exemple d’une série temporelle avec une tendance linéaire de la forme :
Ainsi en différenciant la série une fois , la dépendance temporelle linéaire est éliminée et la différence est stationnaire.
De la même façon, une tendance quadratique peut être éliminée en différenciant la série deux fois.
Une fois la série stationnarisée, il est alors possible d’appliquer le modèle ARMA.
Le modèle ARIMA est donc une combinaison de ce processus de différenciation et du processus ARMA classique.
Par ailleurs, si la série temporelle présente à la fois une tendance et une saisonnalité, il est possible d’utiliser le modèle SARIMA qui est un modèle ARIMA prenant aussi en compte une composante saisonnière.
Et en pratique ça donne quoi ?
On cherche à prédire le nombre de passagers mensuels d’une compagnie aérienne dont on a les données entre 1949 et 1960, Disponible sur Kaggle
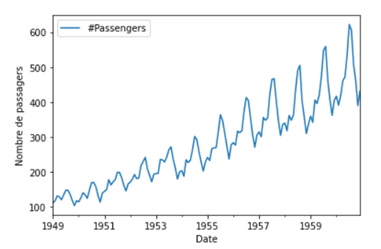
En utilisant la fonction SARIMAX de la bibliothèque statsmodels, il est possible de prédire la série temporelle sur les 15 prochains mois. On choisit de prendre un processus AR d’ordre 1, un processus MA d’ordre 1, une différenciation d’ordre 1 et une saisonnalité sur 12 mois.
Par ailleurs, le modèle permet de calculer un intervalle de confiance de 95% de la prédiction affiché ici en gris
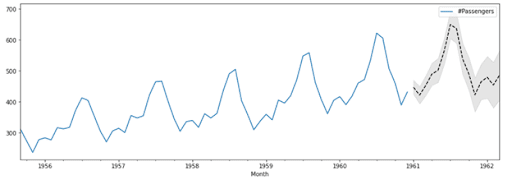
Conclusion :
Plus récemment les réseaux de neurones sont devenus de plus en plus utilisés pour la prédiction des séries temporelles car ils viennent corriger certains défauts des méthodes ‘classiques’ comme l’ARIMA. Découvrez en plus sur les réseaux de neurones en suivant l’une de nos formations.










