Le Quicksort est l’un des meilleurs algorithmes de tri utilisés sur des structures de données de grande taille comme des listes et des tableaux. Découvrez ci-dessous comment fonctionne cet algorithme, quels sont ses différents cas d’utilisation, ainsi que ses performances.
Le tri rapide ou tri pivot est un algorithme de tri inventé en 1961 par Tony Hoare alors étudiant en visite à l’université d’Etat de Moscou.
Parmi les algorithmes de tri les plus connus et les plus utilisés au monde, le tri rapide en fait partie. Le tri rapide (ou Quicksort en anglais) est une technique de tri utilisée pour ranger les éléments d’une structure de données dans un ordre bien précis (croissant ou décroissant). Généralement employé sur des tableaux, il peut aussi être employé sur des listes. Cet algorithme de tri repose essentiellement sur l’approche DPR (Diviser Pour Régner) qui consiste à utiliser deux ou plusieurs tableaux de tailles strictement inférieures à n pour résoudre un problème de tri portant sur un tableau de taille n.
Le tri rapide consiste à choisir d’emblée un élément du tableau à trier qu’on appelle pivot, parfois de manière aléatoire ou de manière spécifique (généralement le premier élément ou le dernier élément du tableau d’entrée). Ensuite il faut partitionner le tableau d’entrée autour du pivot en plaçant le pivot dans sa position correspondante dans le tableau trié c’est-à-dire sa position définitive : ceci est assuré par une fonction de partitionnement. L’algorithme de partitionnement est un algorithme itératif qui parcourt entièrement le tableau à trier afin de placer tous les éléments plus petits que le pivot à gauche de celui-ci et tous les éléments plus grands que le pivot à droite de ce dernier.
Comment fonctionne précisément la fonction de partitionnement ?
De manière itérative, la fonction de partitionnement parcourt le tableau à trier afin de comparer les différents éléments au pivot. Lorsqu’on obtient un élément plus petit que le pivot, on change la position de cet élément avec la valeur d’un élément plus grand que lui apparaissant avant lui dans la liste. Si l’on tombe sur un élément plus grand que le pivot, on ne fait rien.
À l’issue de la fonction Partition, on obtient l’indice du pivot dans le tableau trié qui sera donc son indice final et on permute donc les positions initiale et finale du pivot. Le choix du pivot est crucial car c’est autour de ce dernier que sera réalisée la partition de la structure de données. En effet, si le pivot ne permet pas de diviser le tableau en deux sous-tableaux de tailles approximativement égales c’est-à-dire que si le pivot ne correspond pas plus ou moins à la médiane mais à une borne de l’ensemble à trier, le partitionnement donnera un ensemble de taille vide et un ensemble de taille n-1 si la taille initiale était n.
À la première étape, cette répartition nécessite n opérations. Au coup suivant, elle en nécessitera n-1, puis n-2, jusqu’à ce qu’il ne reste plus rien à trier, ce qui correspond exactement au principe du tri sélection qui a une complexité quadratique. Une idée générique communément admise consiste donc à prendre comme pivot la médiane de trois valeurs prises aléatoirement dans le tableau dans le but de pallier cette situation de choix du mauvais pivot.
Que faire après avoir obtenu la position finale du pivot à l’issue de la fonction de partitionnement ?
Après avoir obtenu la position finale du pivot et permuter les indices, il faut appliquer la fonction de tri rapide sur les deux sous-tableaux obtenus de part et d’autre du pivot.
C’est-à-dire le sous-tableau de gauche repéré par Tableau[début,indice(pivot)-1] et le sous-tableau de droite repéré par Tableau [indice(pivot)+1,fin] où indice(pivot) correspond à l’indice du pivot obtenu à l’issue de la fonction de partitionnement sur le tableau d’entrée.
Il va ensuite falloir choisir deux pivots correspondant aux pivots des sous-tableaux de gauche et de droite, puis appliquer un appel récursif (recursive call en anglais) de la fonction de tri rapide sur ces deux sous-tableaux. Les appels récursifs dans la fonction Quicksort vont s’arrêter soit lorsque l’indice de début et de fin d’un sous-tableau seront égaux, auquel cas le tableau contient un seul élément et par ricochet est déjà trié, soit lorsque l’indice de début d’un sous-tableau est supérieur à son indice de fin auquel cas le tableau ne contient aucun élément (tableau vide) donc est aussi trié.
Illustration du tri rapide
Considérons pour illustrer l’array ci-dessous où le pivot a été choisi comme l’élément le plus à droite c’est-à-dire array[longueur(array)-1] = 4 :
array = [9, 12, 1, 5, 6, 13, 8, 2, 4]
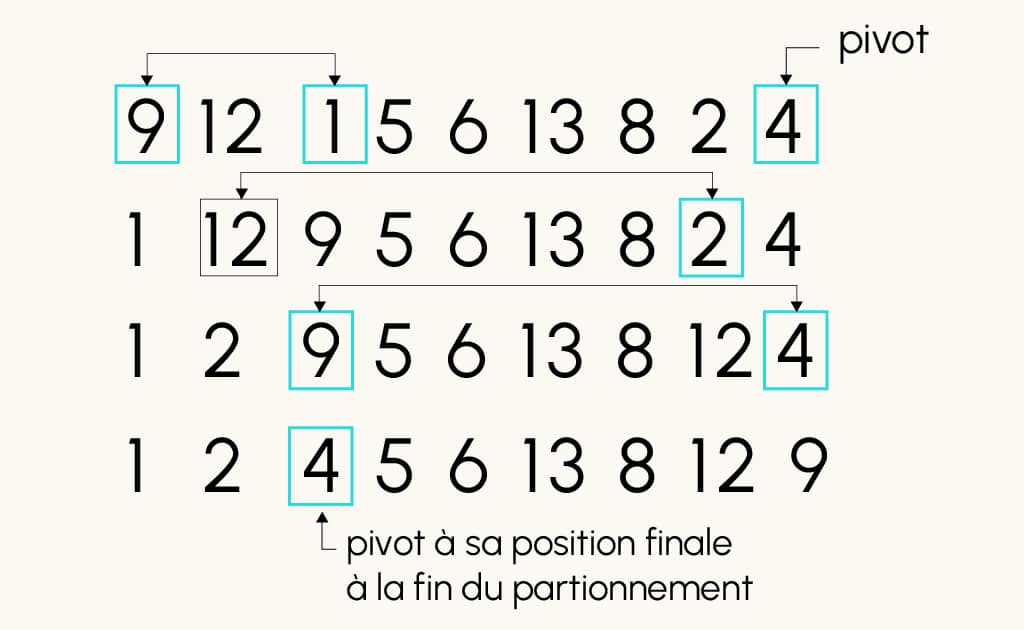
- En appliquant la fonction partition(array, 0, len(array)-1), on obtient :
Tableau partitionné: 1 2 4 5 6 13 8 12 9 où le pivot a été déplacé à sa position finale du tableau trié
- On applique ensuite la fonction quicksort sur les deux arrays obtenus de part et d’autre du pivot:
array1 = [1, 2]
array2 = [5, 6, 13, 8, 12, 9]
Et il faudra aussi choisir un pivot pour chacun de ces arrays puis réaliser les partitions jusqu’à ce qu’ils soient triés.
- On obtient après exécution de fonction quicksort le tableau ci-dessous :
Sorted Array : 1 2 4 5 6 8 9 12 13 En termes de complexité, dans le meilleur des cas et dans le cas moyen, on observe une complexité quasi linéaire c’est-à-dire en O(nlogn). Cependant, dans le pire des cas, le tri rapide présente une complexité quadratique c’est-à-dire en O(n^2) ce qui n’est pas satisfaisant. On observe une complexité quadratique dans cet algorithme lorsque le tableau est déjà trié ou presque trié.
Démonstration de la complexité du tri rapide dans le cas moyen
En partant de l’équation de récurrence satisfaite dans le cas moyen, on peut démontrer que la complexité est quasi-linéaire comme l’illustre la preuve ci-dessous : Pour résoudre un problème de taille n, on résout deux problèmes de taille n/2 avec une reconstruction linéaire due à la fonction de partitionnement qui est linéaire en la taille de la structure de données.
où O(n) représente la complexité de la fonction Partition
En posant n = 2 k , on obtient k = log 2 n
Or, T(1) représente la complexité du tri rapide dans le cas où le tableau contient un seul élément donc trié.
Pourquoi le tri rapide est-il si important ?
Le tri rapide est en moyenne plus efficace qu’un autre pour des raisons de localité de données. En effet, chaque appel va travailler sur des données très proches en mémoire. En raison des caches permettant des optimisations considérables quand les données ont une forte localité, l’algorithme présente des meilleures performances.
Pour ce qui est de la complexité spatiale, le tri rapide a une complexité quadratique dans le pire des cas et une complexité logarithmique dans le cas moyen. Le tri rapide est efficace sur de grandes structures de données et a une faible complexité spatiale. En revanche, il est moins efficace que le tri insertion par exemple sur de petites structures.
En conclusion, le tri rapide ou quicksort est un algorithme de tri très utilisé en particulier sur de grandes structures de données qui présente une bonne complexité temporelle dans le cas moyen. Le choix du pivot lors de l’utilisation de cet algorithme reste cependant un facteur crucial, ce qui nécessite donc de faire un choix adéquat du pivot.










