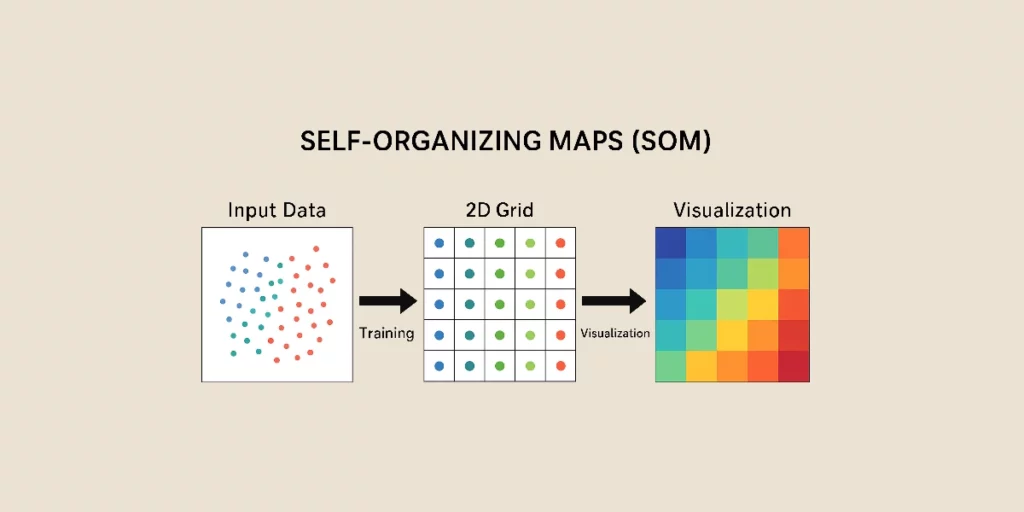
Les Self-Organizing Maps, ou SOM, sont un type de réseau de neurones artificiels (ANN) utilisé pour l’apprentissage non supervisé. Elles permettent de réduire la dimensionnalité des données tout en préservant leur structure topologique, offrant ainsi un puissant outil pour le clustering et l’exploration de données.
Contrairement aux réseaux de neurones classiques, les self-organizing maps fonctionnent par apprentissage compétitif plutôt que par correction d’erreur et intègrent une fonction de voisinage pour maintenir les relations spatiales des données.
Origine des SOM
Les self-organizing maps ont été introduites dans les années 1980 par le chercheur finlandais Teuvo Kohonen. C’est pourquoi elles sont également appelées cartes de Kohonen ou Kohonen maps.
Inspirées des mécanismes biologiques du cerveau, elles imitent la manière dont les neurones organisent et classent les informations pour former des structures significatives.
Fonctionnement des SOM
L’apprentissage d’une Self-Organizing Map repose sur un processus en plusieurs étapes, qui lui permet de transformer des données complexes en une représentation organisée et lisible. Voici un fonctionnement typique, détaillé étape par étape, d’un SOM.
1. Initialisation des poids
Avant de commencer l’entraînement, chaque neurone de la carte est associé à un vecteur de poids, initialisé de manière aléatoire. Ce vecteur a la même dimension que les données d’entrée et représente l’identité de chaque neurone avant qu’il ne soit ajusté par l’apprentissage.
2. Sélection d’un échantillon d’entrée
À chaque itération, un vecteur d’entrée est sélectionné aléatoirement dans le dataset d’entraînement. Ce vecteur représente un point de données que la SOM doit apprendre à organiser sur la carte.
3. Identification du Best Matching Unit
Une fois l’échantillon choisi, l’algorithme recherche le neurone dont les poids sont les plus proches de ce vecteur d’entrée. Cette proximité est mesurée à l’aide de la distance euclidienne ou norme euclidienne entre le vecteur d’entrée et les neurones. Le neurone le plus proche est identifié comme le BMU (Best Matching Unit).

4. Mise à jour des poids du BMU et de ses voisins
Après avoir trouvé le BMU, l’algorithme ajuste ses poids pour les rapprocher du vecteur d’entrée. Ses neurones voisins sont également mis à jour, mais dans une moindre mesure.
L’ampleur de cette mise à jour dépend de deux facteurs principaux :
- Le taux d’apprentissage (noté α ou alpha) : Alpha contrôle la vitesse à laquelle les poids des neurones sont ajustés. Il diminue au fil des itérations pour éviter des changements trop brusques.
- La fonction de voisinage : La mise à jour affecte les neurones situés autour du BMU, et son ampleur diminue avec la distance. Une fonction courante est la fonction gaussienne.
Cette phase permet au BMU et à ses voisins de se rapprocher progressivement des caractéristiques des données, tout en préservant la structure topologique des relations entre les points de données.
5. Réduction du taux d’apprentissage et du voisinage
Au fur et à mesure des itérations, le taux d’apprentissage et la taille du voisinage diminuent. Cela permet un ajustement fin des poids dans les dernières étapes de l’entraînement et garantit que les données sont bien organisées sur la carte.
- Au début, le voisinage est large, permettant à l’ensemble de la carte de s’organiser globalement.
- Progressivement, le voisinage se rétrécit, affinant la carte et stabilisant les clusters formés.
6. Convergence et stabilisation
L’entraînement se poursuit jusqu’à ce que la carte atteigne un état stable, où les poids des neurones ne changent plus significativement d’une itération à l’autre. À ce stade, chaque neurone représente une région spécifique des données d’entrée.
7. Inférence et visualisation des résultats
Une fois la SOM entraînée, elle peut être utilisée pour organiser de nouvelles données et en faciliter l’analyse visuelle. La distance entre un vecteur d’entrée et les poids des neurones permet de déterminer où se situe une nouvelle donnée sur la carte.
Une méthode courante pour visualiser les SOM consiste à attribuer des couleurs aux différentes régions de la carte. Plus la couleur est sombre, plus la concentration de données est importante.
Les clusters de données similaires apparaissent clairement sur la carte, offrant une visualisation intuitive des relations entre les différentes catégories.
Avantages et Inconvénients des SOM
Les SOM offrent plusieurs avantages notables. Elles permettent de réduire la dimensionnalité des données tout en conservant leur organisation topologique. Grâce à leur représentation graphique intuitive, elles facilitent la visualisation et l’interprétation des dataset complexes. Elles sont souvent utilisées pour effectuer du clustering, même sans connaissance des classes présentes dans les données.
Cependant, les SOM ont certaines limites. Elles s’adaptent mal aux données purement catégoriques ou mixtes (sauf après encodage approprié), qui ne suivent pas une logique dans l’espace de représentation. Leur temps d’entraînement peut être long et leur performance dépend du bon réglage des paramètres.
Applications des SOM
Les SOM sont utilisées dans divers domaines pour organiser et analyser les données. Par exemple dans le secteur du marketing, où elles permettent de regrouper des clients selon leur comportement d’achat afin d’optimiser les stratégies commerciales.
En réduction de dimensionnalité, elles facilitent la cartographie de données haute dimension. Cela permet une meilleure compréhension des relations internes aux données.
Dans la détection d’anomalies, elles sont utilisées pour repérer des transactions frauduleuses en identifiant les points de données qui ne correspondent à aucun cluster prédéfini.
Pour la visualisation des données, elles aident à mieux comprendre les populations et les relations entre différents paramètres. En transformant un dataset complexe en une représentation 2D, elles permettent d’identifier rapidement des tendances et des patterns invisibles dans des tableaux bruts.

Conclusion
Les SOM sont un outil puissant pour l’apprentissage non supervisé dans l’analyse de clusters, la réduction de dimensionnalité et la visualisation des données. Elles ont des limitations, en termes de temps d’entraînement et d’adaptation aux données mixtes. Elles sont utilisées en finance, marketing, santé et analyse d’images. Leur capacité à révéler des structures cachées dans les données en fait un choix incontournable pour l’exploration des données non étiquetées.