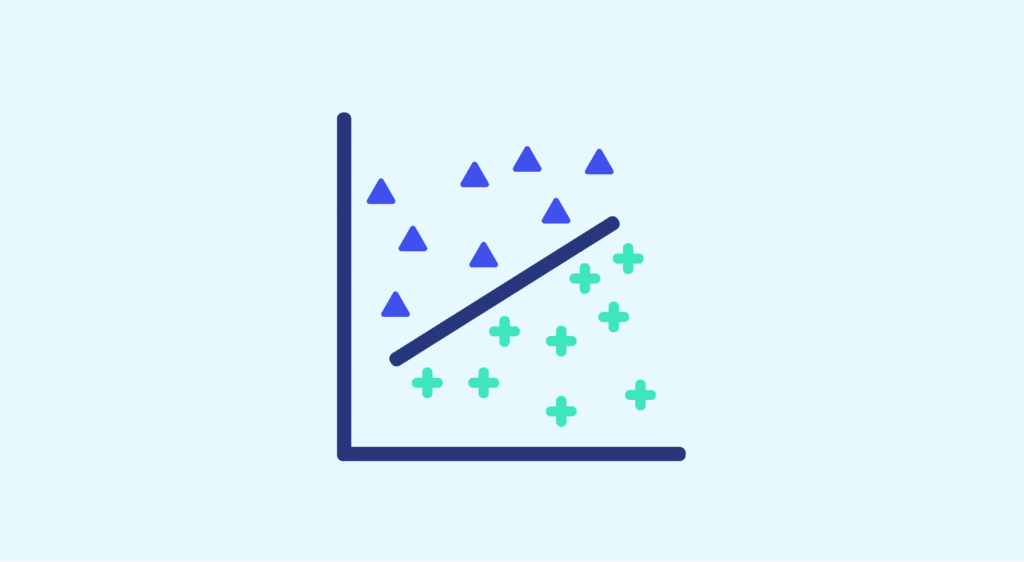
Bienvenue dans la seconde partie de ce dossier dédié au Support Vector Machine.
Dans l’article précédent, nous avions détaillé le fonctionnement et les principaux défauts des Maximal Margin Classifier.
Notre objectif maintenant est d’autoriser notre algorithme à réaliser un certain nombre d’erreurs lors du choix de la droite de séparation. On parle alors de « soft margin », que l’on pourrait traduire par « marge souple ». Nous allons maintenant détailler le fonctionnement de l’algorithme Soft Margin Classifiers, à mi chemin entre le Support Vector Machine et le Maximal Margin Classifier.
Soft Margin Classifiers
Dans le précédent article, nous avions défini ce qu’était la marge, c’est-à -dire la distance qui sépare une droite de l’observation la plus proche.
Dans cette deuxième partie, nous utiliserons aussi le terme de marge mais il désignera cette fois l’ensemble des points plus proches de la droite que l’observation la plus proche.
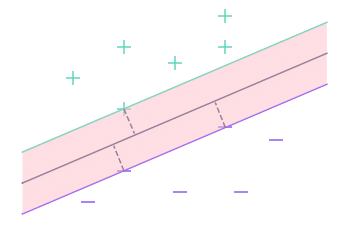
Ici par exemple, la marge est l’aire en rose sur le graphique. Il s’agit en fait de l’espace qui sépare les 2 droites extérieures.
Pour rendre notre algorithme plus flexible, nous allons utiliser un seuil, qui correspond au nombre d’observations que nous tolérerons à l’intérieur de la marge. On cherche ensuite à déterminer, comme précédemment, la droite de séparation qui maximise la marge. Mais on ne se soucie plus désormais des observations qui se trouvent à l’intérieur de la marge. Cela nous permet d’obtenir une certaine insensibilité aux valeurs extrêmes.
Voici ce que l’on obtient dans l’exemple précédent avec des valeurs de seuil différentes :



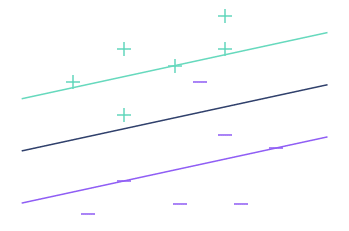
Comme on pouvait s’y attendre, le fait d’augmenter le seuil augmente la marge.
Néanmoins, ceci ne veut pas dire pour autant que la classification est meilleure. On utilise alors la validation croisée pour choisir le meilleur seuil possible.
Si vous n’avez jamais entendu parlé de validation croisée (ou cross validation), en voici une définition rapide.
En réalité, lorsque l’on augmente le seuil, on diminue la variance mais on augmente le biais. Dans le jargon, on dit que plus le seuil est élevé, plus le risque d’overfitting est faible.
Remarque : Les observations qui se trouvent à l’intérieur et aux frontières de la marge sont appelées vecteurs supports (ou Support Vectors), et l’algorithme Soft Margin Classifiers s’appelle aussi Support Vectors Classifier.
Support Vector Machine
Nous avons trouvé une solution au premier problème, mais pas au second. Ainsi, l’algorithme Support Vector Classifier ne fonctionne toujours pas dans le cas suivant :

En fait, lorsque l’algorithme ne fonctionne pas, on dit que les données ne sont pas linéairement séparables, et il existe des outils mathématiques pour déterminer si un jeu de données est, ou n’est pas linéairement séparable.
Lorsque l’on fait face à un jeu de données, on utilise donc ces outils. Si le jeu de données est linéairement séparable, pas besoin d’aller chercher très loin, on applique Soft Margin Classifier. Les choses se corsent en revanche lorsque le jeu de données n’est pas linéairement séparable.
Pour simplifier la visualisation, nous allons changer le jeu de données, et prendre cette fois des observations de dimension 1, c’est-à-dire sur un droite (et pas un plan).
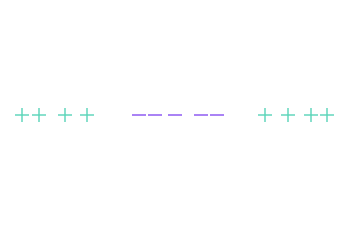
Inutile de vous expliquer pourquoi aucune droite ne peut séparer les « + » et les « – » dans cette configuration particulière.
L’idée du Support Vector Machine est de projeter les données dans un espace de plus grande dimensions, pour les rendre séparables.
Reprenons notre exemple en dimension 1. Nous allons projeter les données dans un espace de dimension 2. Pour ce faire, nous aurons besoin de ce que nous appelons une fonction noyau (ou kernel function). Cette dernière va servir d’intermédiaire entre les deux espaces.
Prenons par exemple comme fonction noyau la fonction cube (f(x) = x^3). Voici comment appliquer la fonction noyau sur le jeu de données pour le projeter dans un espace de dimension 2 :
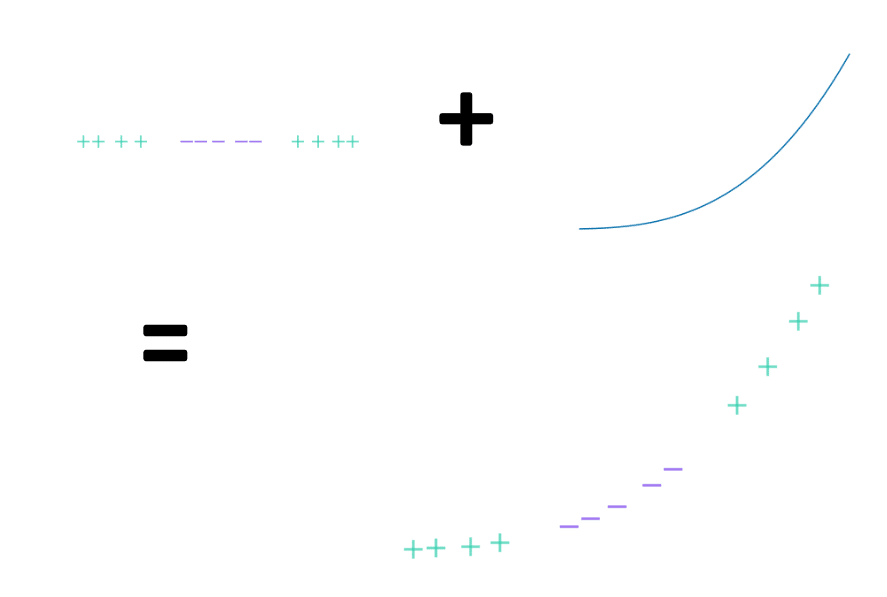
Autrement dit, si l’on note f la fonction noyau, pour chaque observation x, on place un point de coordonnées (x, f(x)) dans le plan.
Le jeu de données projeté est maintenant séparable comme le montre l’image suivante. On peut utiliser l’algorithme Soft Margin Classifiers dont on a explicité le fonctionnement précédemment pour calculer la meilleure droite de séparation et le tour est joué.

Nous venons de détailler le fonctionnement des Support Vector Machine. Et même si nous avons volontairement passé certains détails sous silence (notamment concernant le choix de la fonction noyau), vous avez désormais une vue d’ensemble sur le sujet.
Les algorithmes de SVM peuvent être adaptés à des problèmes de classification portant sur plus de 2 classes, et à des problèmes de régression. Il s’agit donc d’une méthode simple et rapide à mettre en œuvre sur tout type de datasets, ce qui explique certainement son succès. Là où un réseau de neurones demande un travail en amont pour déterminer la bonne structure et les bons paramètres à utiliser, les SVM obtiennent de bons résultats même sans préparation. Si vous souhaitez en apprendre plus sur le Machine Learning, je vous invite à regarder cet autre article qui détaille le fonctionnement des algorithmes de Boosting.