Vous avez toujours été bon en mathématiques depuis l’enfance mais n’avez jamais utilisé vos connaissances à part les calculs mentaux ? Vous vous êtes toujours demandé à quoi cela servait de connaître la dérivée d’une fonction, à part assurer une bonne note à votre examen ? Ou êtes-vous tout simplement fasciné par le monde des mathématiques mais n’arrivez pas à en trouver d’applications concrètes, alors cet article est fait pour vous !
Nous allons présenter ici les 10 notions mathématiques à maîtriser pour pouvoir faire de la Data Science, avec à chaque fois un exemple concret afin que vous puissiez directement voir la mise en œuvre et l’utilité de cette notion. Le monde des mathématiques appliquées à la Data Science est en effet très vaste, donc si vous ne deviez retenir que 10 notions, les voici !
Logique en général
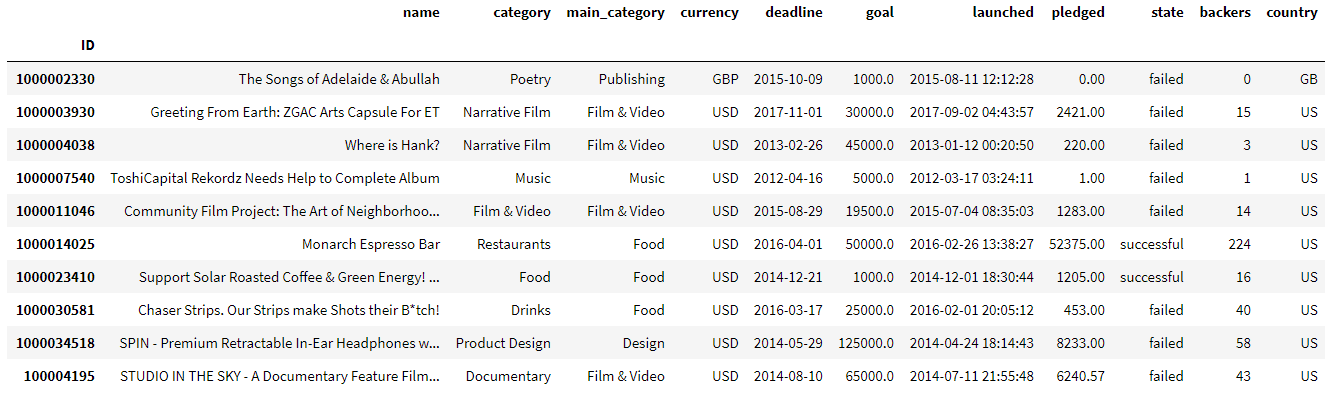
Imaginons un jeu de données nous donnant des caractéristiques sur des campagnes de crowdfunding, dont les 10 premières lignes sont les suivantes, avec chaque ligne représentant une campagne en particulier :
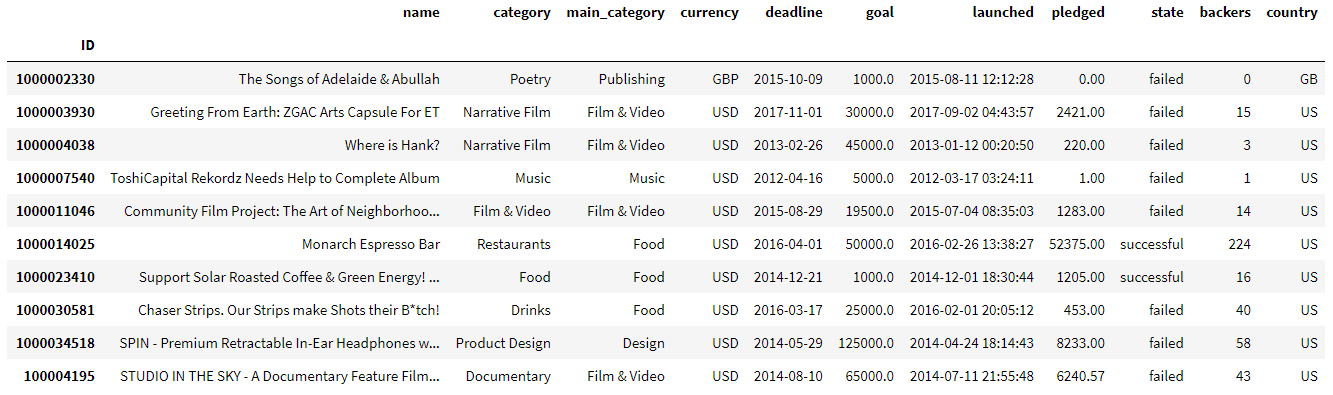
Supposons que vous vouliez choisir dans ce jeu de données toutes les campagnes ayant réussies, cela est simple me direz-vous. Il suffit alors d’appeler ce jeu de données df et écrire l’instruction suivante :
![]()
On obtient ainsi :

Mais les choses se complexifient dès lors que le nombre de conditions augmente et que les opérateurs logiques telles que « ET » (and) et « OU » (or) se multiplient au sein d’une même condition. Une grande capacité réflexive ainsi qu’une bonne organisation sera alors nécessaire afin de ne pas vous mélanger les pinceaux lors de l’écriture de vos conditions.
Voici un exemple :
Statistiques et probabilités
Quand vous entendez moyenne, médiane, quartiles, variance ou encore écart-type, cela vous fait peut-être penser à votre brevet des collèges en 3ème. Quel est le rapport avec la Data Science ? Eh bien ces notions que l’on a tous appris très tôt vont nous servir à mieux connaître nos jeux de données.
En se basant sur l’exemple du jeu de données des campagnes de crowdfunding précédent, intéressons-nous aux 3 colonnes ‘goal’, ‘pledged’ et ‘backers’ qui nous donnent des informations respectivement sur l’objectif de la campagne de crowdfunding, l’argent total collecté pendant la campagne, ainsi que le nombre de contributeurs.
La maîtrise des statistiques descriptives peut justement nous permettre de produire un tel tableau :

Nos très simples notions de statistiques de 3ème nous ont ainsi permis de comprendre que dans notre jeu de données, il y a une majorité de petites campagnes qui échouent (l’argent collecté est en moyenne très inférieur à l’objectif fixé), ainsi qu’une très petite minorité de « grosses campagnes » qui tirent la moyenne vers le haut. En effet, la moyenne des objectifs, de l’argent collecté et du nombre contributeurs sont d’environ 39000, 11267 et 110, contre une médiane de 5000, 650 et 12 pour ces 3 variables.
Toujours par rapport à l’exemple précédent sur les campagnes de Crowdfunding, la notion de statistique inférentielle et notamment les tests d’hypothèse, permettant de déterminer si une variable catégorielle et une autre variable continue sont indépendantes ou non par exemple.
Plus concrètement, faisons attention à la variable ‘main_category’. Le but est de savoir si cette variable qui nous donne des informations sur la catégorie principale de la campagne de crowdfunding en question influe sur le nombre d’argent collecté (‘pledged’). Un test d’hypothèse par la méthode ANOVA (Analysis of Variances) permet d’obtenir un tel tableau :

La p-value (PR(>F)) est inférieur à 5%, on peut donc conclure que la catégorie d’une campagne influe effectivement sur l’argent collecté lors de celle-ci. Cette notion mathématiques pourra notamment nous permettre lors d’une future analyse de cibler les catégories qui permettent de maximiser la récolte d’argents par exemple.
Le théorème de Bayes, fondement des probabilités conditionnelles, est énormément utiliser en Data Science lorsque l’on a affaire à des jeux de données dans le domaine de la médecine, en épidémiologie notamment. Cette notion mathématiques permet par exemple de répondre à une telle question :
Si Michel passe un test PCR covid-19 et que l’on suppose que ce test à une exactitude de 99% : si vous avez le covid, alors vous allez être testé positif dans 99% des cas, et si vous n’avez pas le covid, alors vous allez être testé négatif dans 99% des cas. Si 1% de toute la population mondiale (c’est plus malheureusement mais bon) a le covid et que Michel est testé positif, quelle est la probabilité pour que Michel ait effectivement le covid ?
Réponse :
Posons les événements suivants :
– A : Avoir le covid
– B : Être testé positif
Le théorème de Bayes est donné par la formule suivante :

En remarquant que :
![]()
On peut réécrire le théorème de cette manière :
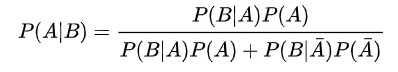
Et ainsi répondre à cette question :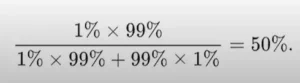
Vous avez à disposition un jeu de données concernant des joueurs de NBA et leurs performances pour la saison 2013-2014 :
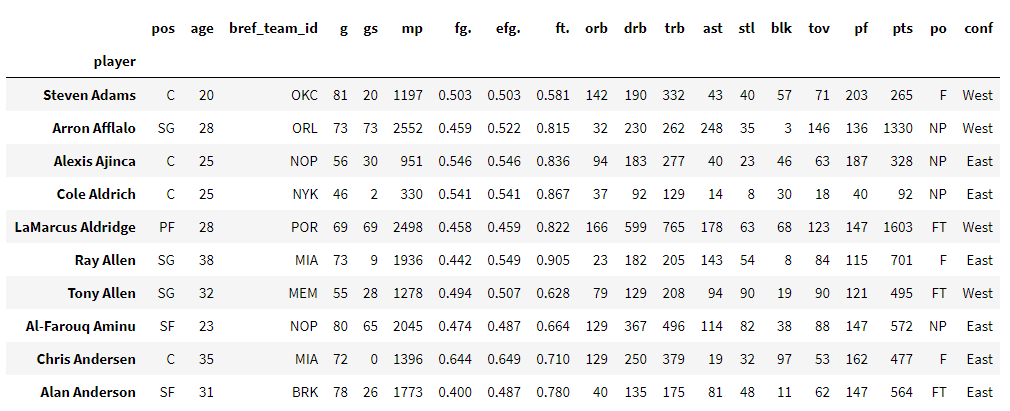
Si on veut savoir un peu mieux comment se répartissent les âges de ces joueurs pendant cette saison, il suffit d’afficher un histogramme de la variable ‘age’ :
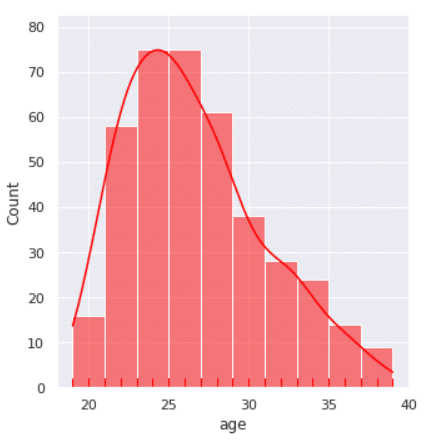
Une courbe d’estimation de la densité a également été ajouté en rouge et épouse la forme de notre histogramme. Ainsi, on peut voir que l’âge des joueurs est réparti entre 19 et 39 ans, avec une majorité de joueurs entre 24 et 26 ans.
Une manière simple et surtout très visuel de voir comment les variables sont liées (« corrélées » pour utiliser le vocabulaire approprié) entre elles est d’afficher une carte des chaleurs des corrélations (‘heatmap’ en anglais) :
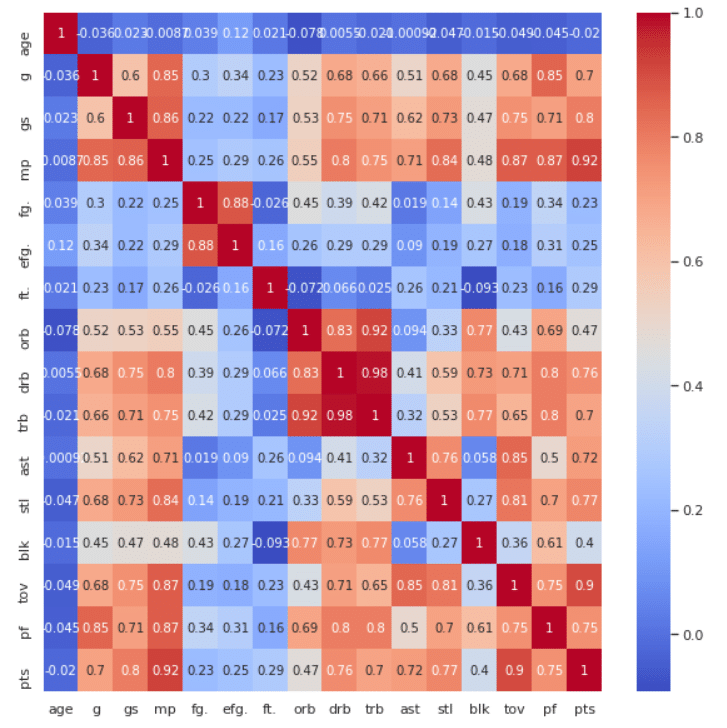
On peut ainsi directement voir que les variables ‘drb’ et ‘trb’, correspondant respectivement à ‘Defensive Rebounds’ (le nombre total de rebonds défensifs) et ‘Total Rebounds’ (le nombre total de rebonds) ont une corrélation très forte de 0.98. Cette corrélation positive pratiquement parfaite signifie que plus ‘drb’ augmente, plus ‘trb’ augmente également. Cela paraît effectivement évident maintenant que l’on a explicité à quoi correspondait ces noms de variables, mais regardez par exemple les deux variables ‘stl’ (Steals = Interception) et ‘pts’ (Points). Elles ont une corrélation assez forte de 0.77, mais cela était beaucoup moins évident en regardant simplement le nom de ces variables ou encore notre jeu de données sans visualisation. Cette dernière analyse de corrélation nous a ainsi permis de remarquer que dans notre jeu de données, les interceptions conduisent généralement à des points, d’où l’importance majeure d’une bonne cohésion d’équipe défensive.
Si vous disposez d’un dé non pipé à 6 faces, et que vous le lancez 20 fois, la somme finale en additionnant chaque résultat sera forcément comprise entre 20 et 120. Comment calculer facilement la probabilité que la somme des résultats obtenus soit supérieur à 100 ? Eh bien le théorème de la limite centrale, qui énonce que si on assemble un grand nombre de variables aléatoires identiquement distribuées par addition, plus la distribution de probabilité de la nouvelle variable sera proche d’une distribution normale :
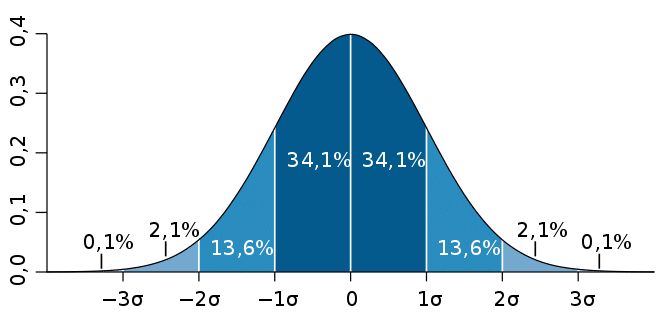
Cela tombe bien, nous avons justement une distribution uniforme pour notre dé à 6 faces avec 1/6 la probabilité d’obtention de chaque face.
Posons X la variable aléatoire qui représente la somme des valeurs des 20 dés.
Tout d’abord, définissons la moyenne et la variance de la loi normale qui caractérise X :
– La valeur moyenne d’un dé, c’est 3.5, donc celle de 20 dés est de 70.
– La variance d’un dé est de 35/12, donc celle de 20 dés est de 700/12.
X suit donc une loi Normale N(70, 700/12)
Il faut alors centrer et réduire X afin de pouvoir utiliser la table de valeurs de la loi Normale Centrée Réduite N(0, 1).
Finalement, P(X >= 100) = P(Z >= 3.93) = 0.000043.
On peut donc s’entendre sur le fait qu’il y a effectivement extrêmement peu de chances d’obtenir un score total de plus de 100 points après avoir lancé le même dé 20 fois.
Analyse et algèbre linéaire
Nous arrivons au point où vous allez enfin pouvoir utiliser les dérivées dont je parlais en introduction 🙂
La notion de dérivée servira en effet à comprendre une des méthodes les plus utilisées aujourd’hui afin de permettre à un modèle de machine learning (d’apprentissage automatique), eh bien, « d’apprendre ». Toutefois, pour que cet article ne soit pas trop long, il faut au moins comprendre.
Prenons un modèle de machine learning permettant d’effectuer des prédictions, tel que la régression logistique, et appelons f(X) la fonction qui décrit les erreurs entre les valeurs réelles et les prédictions faites par notre modèle.
N.B : Cette fonction qui décrit l’erreur de notre modèle est plus communément appelé « fonction de coût » (‘Loss function’, en anglais)
Le but ici est donc d’apprendre à votre modèle de machine learning comment minimiser cette erreur, selon un paramètre que l’on va nommer X, il s’agit ainsi d’un problème d’optimisation de cette variable X.
Une première méthode est de calculer toutes les valeurs de X, ce qui nous donne la courbe en noir dans la figure n°…. Vous vous dites que cette méthode peut fonctionner si X admet un nombre de valeurs bien définis à l’avance, il suffira ainsi de calculer toutes les possibilités. Mais dans le cas où X est une variable continue, donc admettant un nombre infinie de valeurs, cette méthode trouve tout de suite ces limitations.
Un autre moyen de calculer le minimum de cette fonction f(X) est donné par l’algorithme de la Descente de Gradient (‘Gradient Descent’ en anglais).
On commence par initialiser X à une certaine valeur de manière aléatoire, appelons cette première valeur de X le « point de départ ». Cette valeur de départ est X = 0.57 dans notre cas. Calculons ensuite le gradient (ou la dérivée tout simplement, dans le cas d’une seule variable à optimiser) de cette fonction f(X) au point de départ, on obtient une valeur de -2.3 (cette valeur est fictive, c’est juste pour expliquer le principe). Cette valeur de -2.3 est donc la pente de la courbe f(X) au point X = 0.57.
Cette pente peut ainsi nous permettre de calculer ce que l’on appelle le « pas »
pas = pente de la courbe * taux d’apprentissage.
Le taux d’apprentissage est une valeur que nous pouvons fixer arbitrairement, disons 0.1.
Ainsi, pas = -2.3 * 0.1 = -0.23.
Grâce à ce pas, nous pouvons alors obtenir une nouvelle valeur de X, tel que :
Nouveau X = Ancien X – pas = 0.57 – (-0.23) = 0.8.
Ce processus est alors répété à chaque itération comme vous pouvez le voir sur la courbe juste en-dessous, jusqu’à ce que la valeur de l’erreur donnée par la fonction f(X) soit la plus basse parmi les itérations, ce qui représente la valeur optimale du paramètre X :
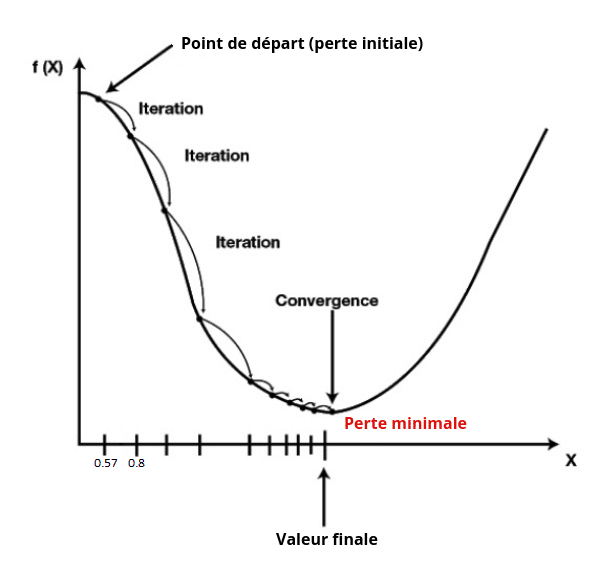
Si jamais le minimum de la courbe n’est pas trouvé, on peut décider d’arrêter l’algorithme, soit quand le pas devient trop petit (généralement plus petit que 0.001), soit si le nombre d’itérations dépasse un nombre fixé (généralement supérieur à 1000).
Pour visualiser cette algorithme plus en détails, étape par étape, je vous laisse consulter cette excellente vidéo du statisticien et youtuber Josh Starmer.
Vous vous êtes toujours demandé comment faisait le géant Google pour déterminer si votre site web est bien référencé ou non, autrement dit : est-ce qu’il est situé parmi les premiers lien lors d’une recherche ?
Eh bien les fondements de ce système provient d’un algorithme appelé PageRank. Son fonctionnement (simplifié) est le suivant :
Imaginez que vous soyez dans une situation où vous disposez de 4 pages web, comme ci-dessous :
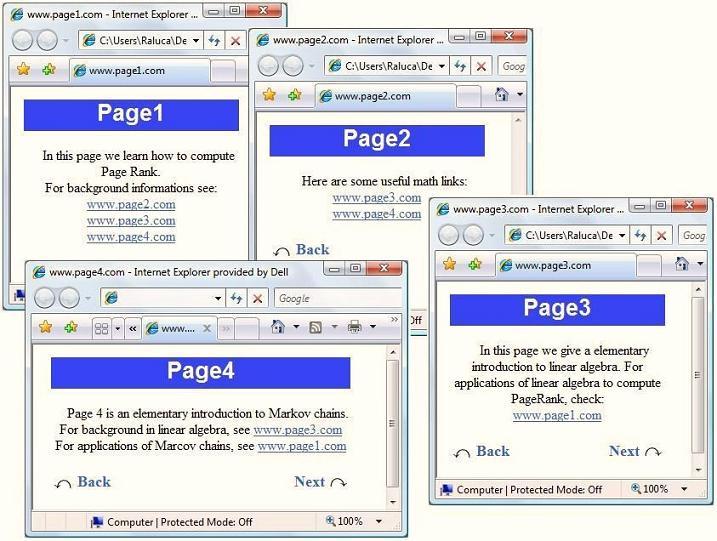
Vous remarquez que chaque page (numérotées de 1 à 4) affichent des liens qui « renvoient » sur d’autres pages.
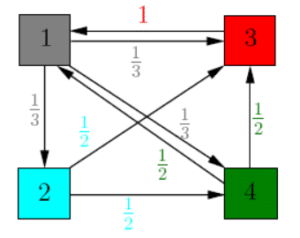
Cette situation peut se schématiser par le graphe suivant :

La première étape est de rajouter à ce graphe des coefficients, correspondant au transfert d’importance de chaque page vers une autre. Par exemple, la page 3 n’à qu’un seul lien qui renvoie vers la page 1, elle transmet donc toute son importance à cette page. A contrario, la page 1 renvoient vers 3 autres pages, elle va donc transmettre son importance de manière uniforme à ces 3 pages, ce qui correspond à 1/3 pour chacune. On peut ainsi résumer chaque importance relatif de la manière suivante :
Appelons ainsi A, la matrice correspondant aux poids transférés de chaque page vers les autres, ainsi :
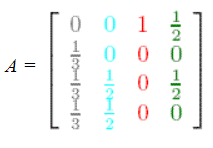
Si on note ensuite x1, x2, x3 et x4 le « rank » de chaque page, on résout ainsi le système suivant :
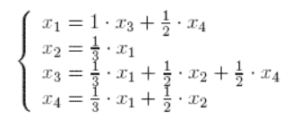
Ce qui équivaut à résoudre, d’un point de vue matriciel, le système suivant :
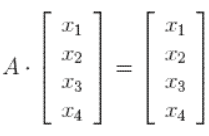
Cela nous tout de suite penser à l’utilisation des valeurs et vecteurs propres, car nous sommes en effet dans le cas où on a A.v = z.v avec avec v le vecteur propre correspondant à la valeur propre z.
Or on sait que les vecteurs propres correspondant à la valeur propre z = 1 sont de la forme (cf. exemple 6 de ce lien) :
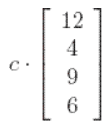
Le principe du PageRank est de ne refléter que l’importance relative de chaque page entre elles. Choisissons donc c = 1/31 (avec 31 = 12 + 4 + 9 + 6) afin que v soit le vecteur propre unique dont la somme de toutes les entrées est égale à 1. La solution de notre système est donc :
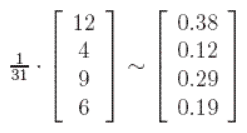
Cela signifie ainsi que la page 1 a le plus haut rang, ensuite la page 3, puis 4 puis enfin la deuxième page.
Cet exemple est évident très simpliste mais permet d’avoir une bonne intuition de la manière dont l’utilisation de l’algèbre linéaire et plus particulièrement les opérations matrices-vecteurs, permettent de résoudre des cas concrets d’entreprise.
Le principe de la décomposition en valeurs singulières est une notion pouvait aider notamment à créer un système de recommandations, en se basant sur l’idée de factoriser une matrice.
Supposons que vous soyez une entreprise très connue dont on ne va pas citer le nom, proposant des films et séries en streaming. Vous pouvez considérer votre jeu de données comme une matrice dont les lignes sont les identifiants de vos utilisateurs (userId) et les colonnes sont les identifiants de vos films (movieId) :

Les valeurs dans les cases correspondant à une note sur 5 attribuée à chaque couple (userId, movieId). Mais comme vous pouvez le remarquer, beaucoup de données sont manquantes (les cases vides), on ne peut donc pas utiliser la méthode de décomposition en valeurs singulières. Ces données manquantes représentent les films qui n’ont pas été notées par certains utilisateurs.
Nous allons donc factoriser cette matrice en 2 matrices aléatoires de dimensions inférieures, comme sur cette image :
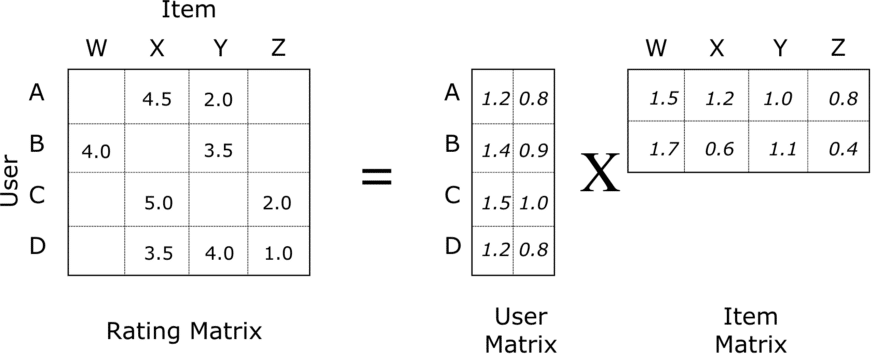
En remultipliant ces 2 matrices, nous allons retomber sur la première matrice, avec cette fois-ci toutes les cases remplies. C’est ainsi que notre modèle va pouvoir prédire des notes pour certains films que les utilisateurs n’auront pas vu.
Evidemment, comme la factorisation de notre première matrice a été faite de manière aléatoire, et en comparant les vraies notes dans les cases existantes avec celles prédites pour chaque couple (userId, movieId), l’erreur va être très grande. Heureusement, l’algorithme de Descente de Gradient va aider à corriger cet erreur petit à petit, sur le même principe qu’expliqué précédemment dans la notion n°8.
Lorsque l’erreur de notre modèle est suffisamment basse, nous allons ordonner ces notes prédites par ordre décroissant (les meilleurs notes en premier), nous pouvons proposer à nos utilisateurs des recommandations adaptées.
Plus de détails sont donnés dans ce très bon article du Data Scientist Kevin Liao.
Des cours sur les systèmes de recommandations sont également disponibles dans la dernière étape « Systèmes complexes et IA » du cursus Data Scientist de chez DataScientest.
Enfin, j’ai également moi-même rédigé un article concernant la réalisation de A à Z d’un système de recommandations de films, que je vous invite à consulter à travers ce lien.










