Les autoencodeurs sont des réseaux de neurones non supervisés conçus pour compresser puis reconstruire des données. Leur architecture repose sur deux parties : un encodeur, qui réduit la dimensionnalité, et un décodeur, qui tente de reconstruire l’entrée initiale.
Des autoencodeurs aux VAEs
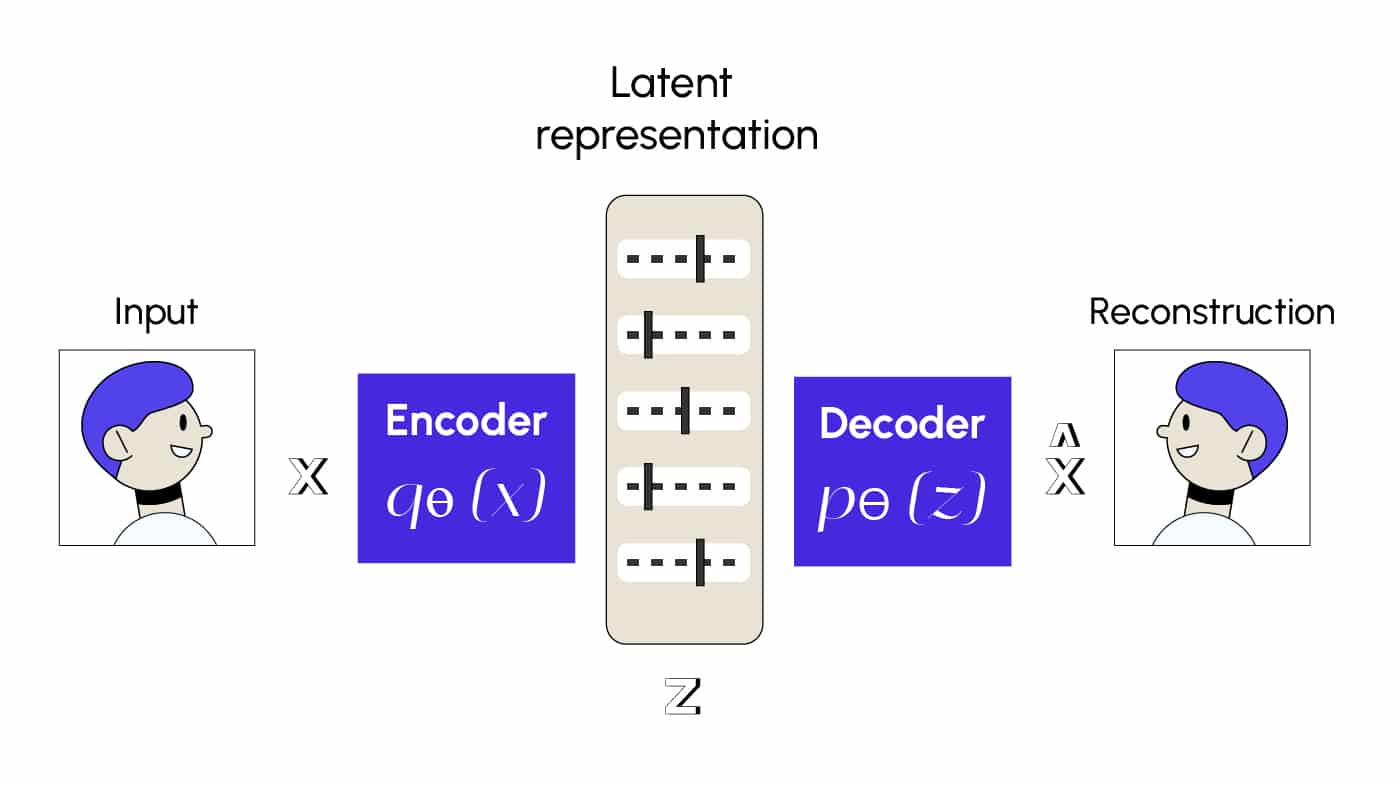
L’autoencodeur classique apprend à reconstruire fidèlement une entrée à travers une représentation latente comprimée. Cependant, cet espace latent n’est pas structuré : si on y génère un point au hasard, le décodeur produit rarement une sortie cohérente.
Le Variational Autoencoder (VAE) apporte une solution élégante à ce problème. Il ne cherche pas seulement à compresser les données, mais à apprendre une distribution probabiliste dans l’espace latent, de sorte que chaque point échantillonné ait du sens.
Le cœur du VAE : modélisation probabiliste
L’encodeur d’un VAE ne produit pas un vecteur fixe, mais deux vecteurs :
- une moyenne μ(x)
- un écart-type σ(x)
Cela définit une distribution gaussienne pour chaque donnée d’entrée. On échantillonne un vecteur latent z selon cette distribution :
z = μ + σ ⊙ ε, avec ε ∼ N(0, I).
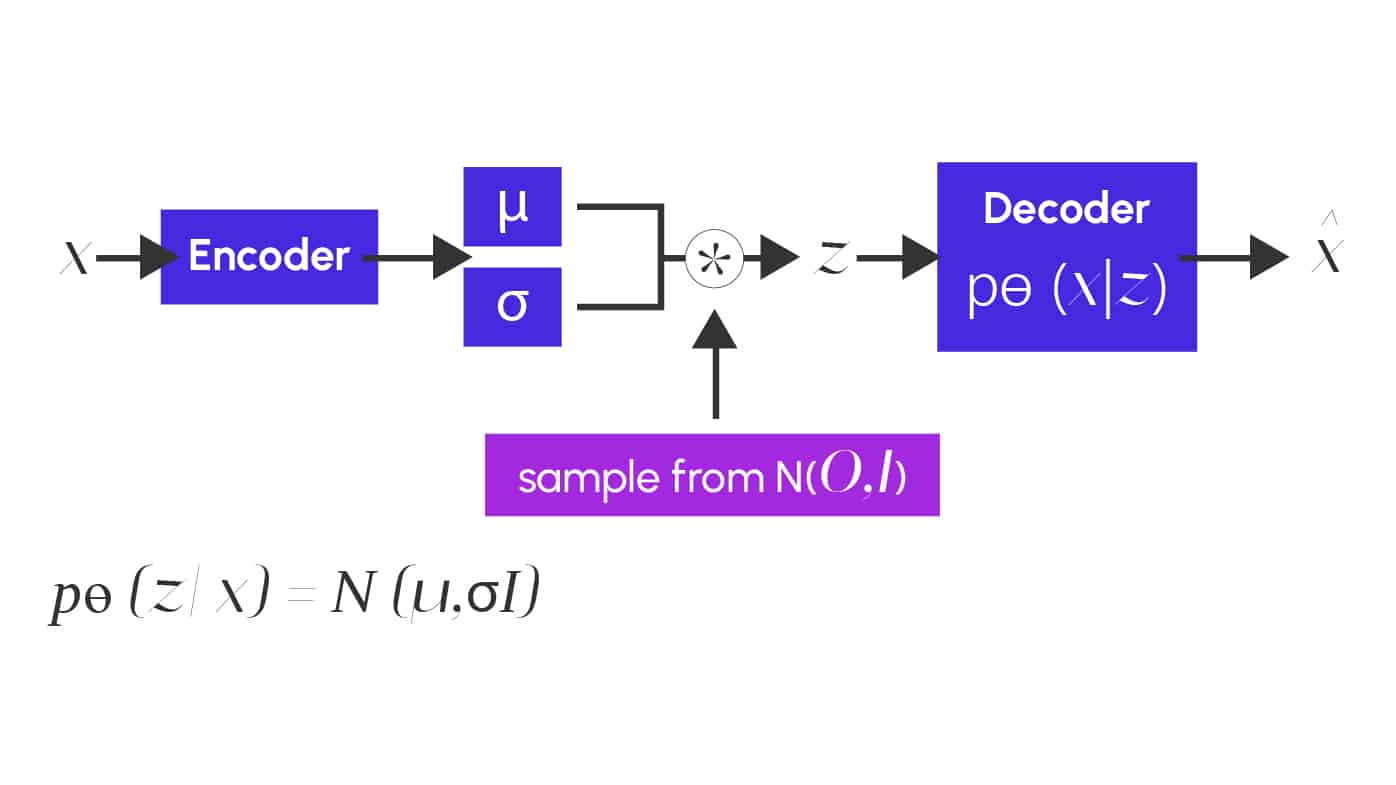
Ce schéma illustre clairement les étapes : encodage, tirage aléatoire depuis une distribution normale, puis décodage.
Le problème : on ne peut pas dériver à travers un tirage aléatoire classique, ce qui bloque l’apprentissage par gradient. Le reparameterization trick contourne cela en exprimant le tirage comme une opération déterministe sur une variable aléatoire fixe (ε), permettant de rendre l’ensemble du modèle différentiable. Ce tour de passe-passe mathématique est ce qui rend le VAE entraînable efficacement avec backpropagation.
Une fonction de perte en deux temps
L’entraînement du VAE repose sur deux objectifs :
- Reconstruction : la sortie doit ressembler à l’entrée
- Régularisation : la distribution latente q(z|x) doit rester proche de la distribution standard N(0, I), via la divergence de Kullback-Leibler (KL)
Cette régularisation permet un espace latent structuré, fluide et génératif. Elle garantit aussi que des interpolations entre points latents produisent des résultats réalistes.
Applications concrètes
Le VAE est utilisé pour :
- Générer des données réalistes : visages, sons, textes
- Interpoler entre des points latents (morphing d’images, par exemple)
- Détecter des anomalies : une donnée mal reconstruite peut signaler un défaut
- Apprentissage semi-supervisé : en ajoutant une tête de classification à l’espace latent
Le VAE est également prisé en data augmentation, notamment lorsqu’il est difficile d’obtenir de grandes quantités de données annotées.

Variantes et limites
Le Variational Autoencoder (VAE), bien qu’efficace pour apprendre des représentations latentes continues et générer des données, présente certaines limites :
- L’espace latent manque souvent de structure, ce qui rend son interprétation difficile.
- Les échantillons générés peuvent être flous ou peu variés.
Pour y remédier, plusieurs variantes ont été développées :
- Le β-VAE renforce la contrainte sur l’espace latent via un coefficient β. Cela favorise des représentations où chaque dimension encode un facteur simple et identifiable (ex. : taille, orientation…), rendant l’espace latent plus interprétable.
- Le VQ-VAE (Vector Quantized VAE) remplace l’espace latent continu par un ensemble de codes discrets appris. Ce format discret est utile pour des tâches comme la compression ou la génération audio, où les données ont des structures répétitives.
Conclusion
Le Variational Autoencoder marie intelligemment compression et génération en encadrant mathématiquement l’espace latent. Il s’impose aujourd’hui comme un outil fondamental du deep learning probabiliste, avec des applications variées et puissantes dans la data science moderne.