Dans cet article nous vous présentons 3 tests statistiques non paramétriques et dans quelles situations les utiliser avec exemples à l’appui.
Vous connaissez le test de Student, le test de Khi-carre ou encore le test de Fisher qui sont des tests paramétriques. Mais pour utiliser des tests statistiques paramétriques, nous devons vérifier certaines hypothèses concernant les échantillons de données (même variances entre les deux groupes d’échantillons donnés, que l’échantillon suit une loi normale…). Parfois on ne peut pas vérifier ces hypothèses statistiques ou alors elles ne sont pas vérifiables, c’est ici que nous utilisons les tests statistiques non paramétriques !
Test de Wilcoxon des rangs signés
Ce test correspond à la version non paramétrique du test de Student. En effet, pour le test de Student, on a besoin du caractère gaussien des données qui n’est pas forcément vérifié : c’est ici qu’intervient ce test !
Cas d’utilisation :
- On dispose d’une population où l’on effectue une expérience aléatoire et on souhaite comparer un avant/après, (évaluation du rythme cardiaque d’une population avant/après l’injection d’un médicament),
- On dispose de deux échantillons appariés. (Comparaison des salaires hommes/femmes de mêmes âges pour le même poste).
Sur python on utilise la fonction scipy.stats.wilcoxon de la librairie scipy avec le module stats.
Exemple :
Nous disposons d’un ensemble de données qui mesure le rythme cardiaque avant et après le don du sang de 8 personnes prises au hasard dans une population. Nous répertorions dans le tableau ci-dessous les données. On cherche à savoir si le rythme cardiaque est plus faible après qu’avant le don du sang, c’est-à-dire que l’on cherche à procéder au test :
Hypothèse nulle H0 : « le rythme cardiaque est le même avant et après le don du sang » et
Hypothèse alternative H1 : « le rythme cardiaque est plus faible après le don du sang qu’avant le don du sang ».

Test de Mann Whitney
Il correspond à la version non paramétrique du test de Student pour deux échantillons indépendants. Il est également appelé le test de Wilcoxon de la somme des rangs ou le test de Wilcoxon-Mann Whitney.
Cas d’utilisation :
- Pour des échantillons indépendants entre eux. (Comparaison des notes de deux classes)
Sur python on utilise la fonction scipy.stats.mannwhitneyu de la librairie scipy avec le module stats.
Exemple :
Une compagnie ferroviaire cherche à comparer le nombre de retards pour deux types de trains : les trains A et les trains B. Dans le tableau ci-dessous est listé le nombre de retards pour chaque train en fonction de leur type A ou B. On cherche à savoir si l’un des deux types de train à tendance à prendre des valeurs plus grandes que l’autre.
L’hypothèse nulle Ho : « Les retards pour les deux types de trains sont similaires » et l’hypothèse alternative H1 : « L’un des deux types de trains a plus de retard que l’autres ».
Test de Kruskal Wallis
Ce test correspond au test de Mann-Whitney pour plus de deux échantillons, on peut le considérer comme la version non paramétrique de l’Anova (modèles statistiques qui permettent de montrer si des groupes appartiennent à la même population).
Cas d’utilisation :
- Comparer la production de blé sur 4 terrains indépendants.
Exemple :
La compagnie ferroviaire cherche à comparer le nombre de retards maintenant pour quatre types de trains : les trains A, B, C, et D. Dans le tableau ci-dessous est listé le nombre de retards par type de trains. Notre but est de déterminer s’il y a des différences significatives de retards entre les différents types de trains.
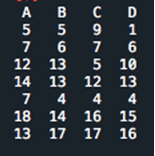
L’hypothèse nulle Ho : « tous les types de trains ont des retards similaires » et l’hypothèse alternative H1 : « L’un des types de trains a plus/moins de retards que les autres ».
Sur python on utilise la fonction scipy.stats.kruskal¶ de la librairie scipy avec le module stats.
Pour conclure, lorsque les hypothèses statistiques pour les tests paramétriques ne sont pas vérifiables ou pas vérifiées, on peut appliquer un test non paramétrique. Ce sont des tests plus robustes qui s’appliquent dans beaucoup de situations, en revanche ils sont en général moins puissants que les tests paramétriques. Si vous souhaitez en savoir plus concernant les tests statistiques, un module y est consacré dans notre formation de Data Analyst ou Data Scientist.










