Vous souhaitez savoir si la moyenne des notes entre deux classes est significativement différente ? Ou savoir si la pollution dans une ville est supérieure à un taux autorisé ? Comment tester l’efficacité d’un nouveau traitement sur une population ? C’est ici que nous utilisons les tests statistiques ! DataScientest vous présente la méthode pour faire un test statistique en 5 étapes avec un exemple à l’appui.
Qu’est-ce qu’un test statistique ?
Un test statistique permet de prendre une décision entre deux hypothèses. À partir de l’hypothèse statistique et d’un échantillon de données, on doit répondre à une certaine problématique.
Dans cet article, on va se baser sur l’expérience suivante : nous disposons d’un ensemble de données qui mesure le rythme cardiaque avant et après le don du sang de 8 personnes prises au hasard dans une population. Nous répertorions dans le tableau ci-dessous les données. On cherche à savoir si le rythme cardiaque est plus faible après ou avant le don du sang.
| Rythme Cardiaque (par minute) | |
|---|---|
| Avant don du sang | Après don du sang |
| 78 | 84 |
| 101 | 80 |
| 77 | 67 |
| 75 | 72 |
| 92 | 79 |
| 76 | 77 |
| 66 | 64 |
| 87 | 80 |
1ère étape : Définir l’hypothèse nulle et l’hypothèse alternative
L’hypothèse nulle Ho correspond à un non-effet de l’expérience. En général cela peut être l’égalité de paramètres statistiques comme la moyenne ou la variance de deux échantillons choisis dans une population. C’est ce que l’on va rejeter ou accepter.
L’hypothèse alternative H1 est l’hypothèse que l’on cherche à montrer. En général, c’est une l’hypothèse ‘opposé’ ou ‘contraire’ à l’hypothèse nulle. Elle affirme que le paramètre utilisé pour l’hypothèse nulle est soit supérieur, soit inférieur, soit différent.
Dans notre exemple, on cherche à savoir si le rythme cardiaque diminue avec le don du sang alors on définit l’hypothèse Ho : « le rythme cardiaque est le même avant et après le don du sang » et H1 : « le rythme cardiaque est plus faible après qu’avant le don du sang ».
2eme étape : L’erreur de première et deuxième espèce et la fonction puissance
Lors d’un test statistique, il faut bien comprendre qu’on n’est jamais sûr à 100% du résultat. Il y a toujours un risque de se tromper.
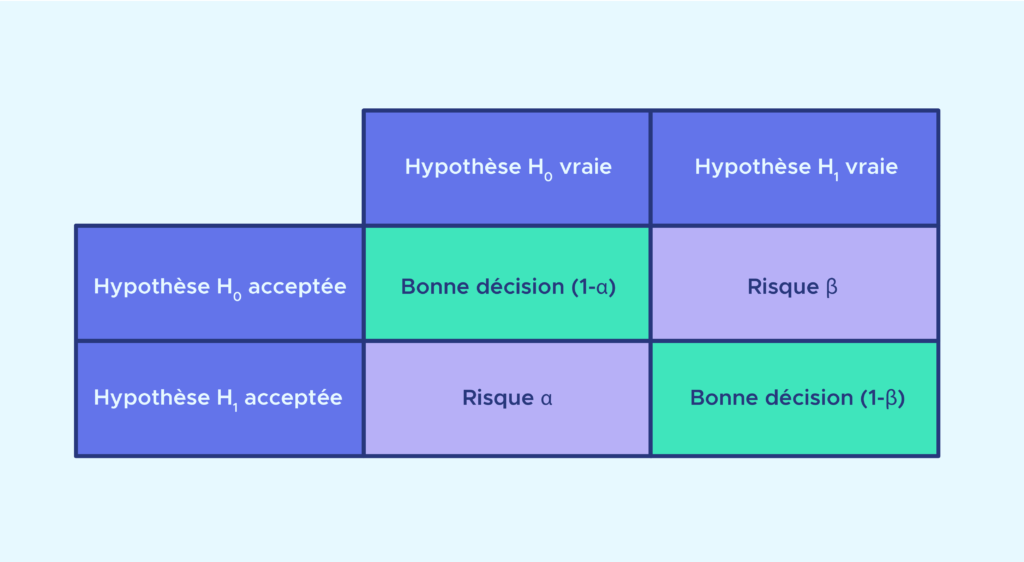
L’erreur de première espèce alpha correspond au risque de rejeter l’hypothèse nulle Ho alors qu’elle est vrai : c’est un « faux positif ».
L’erreur de deuxième espèce beta correspond au risque d’accepter l’hypothèse nulle alors qu’elle est fausse : c’est un « faux négatif ».
La fonction puissance est le risque de rejeter Ho alors qu’on doit en effet rejeter Ho.
Par défaut, on fixe le paramètre alpha à 5% : c’est-à-dire que la probabilité maximale de rejeter HO si elle est vraie est de 5%.
Pour construire un test, on impose que l’erreur de première espèce soit l’erreur la plus importante à prendre en compte. Ainsi parmi tous les tests dont l’erreur de première espèce est plutôt faible, on choisit ceux dont l’erreur de deuxième espèce est la plus petite possible.
3eme étape : Choisir entre un test unilatéral et bilatéral
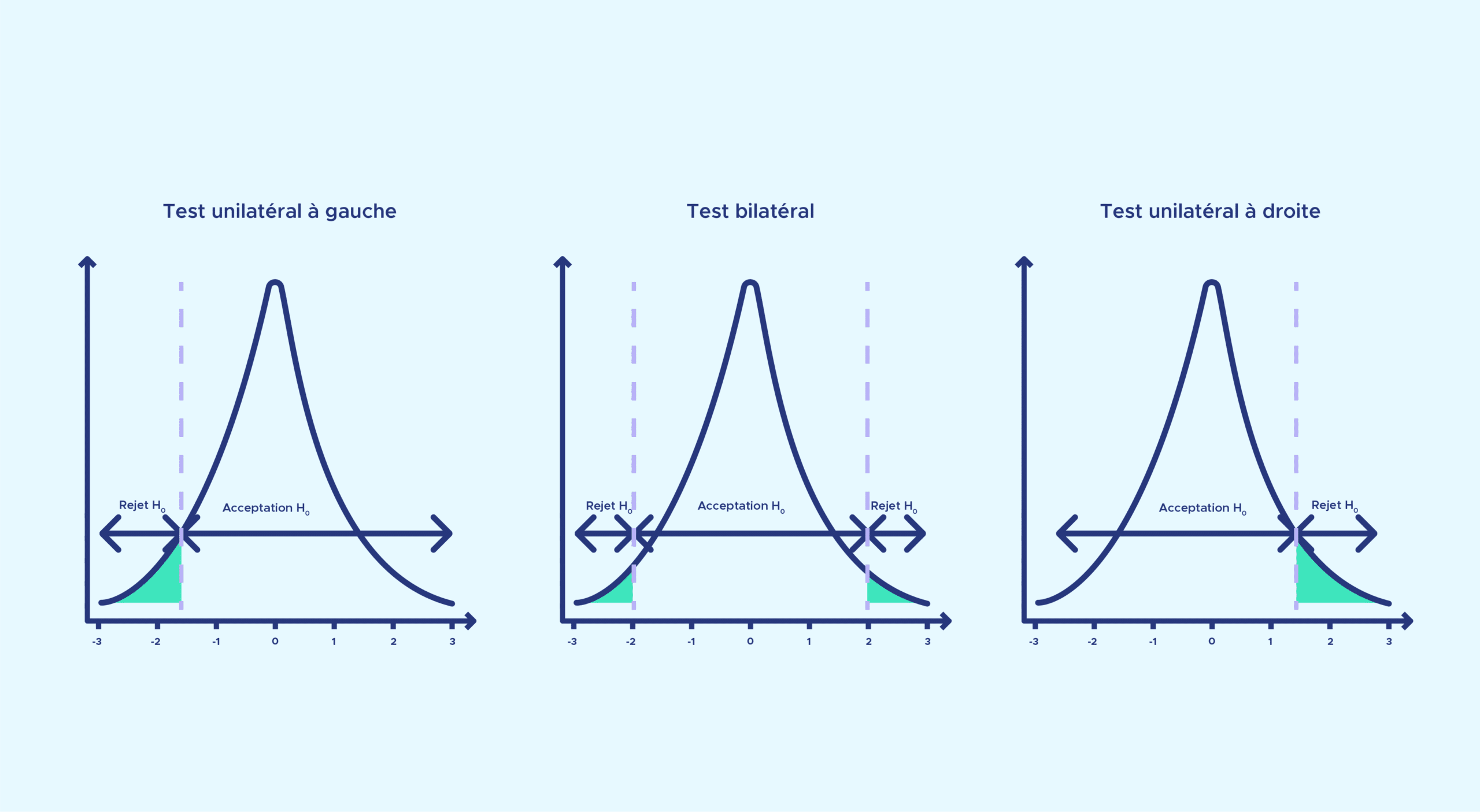
Il existe deux grands types de tests : unilatéral ou bilatéral, qui vont dépendre de la définition des hypothèses.
- Un test unilatéral est un test statistique où le paramètre de l’hypothèse alternative sera soit plus petit, soit plus grand qu’une valeur de référence, par exemple si l’on prend les moyennes de deux échantillons A et B, ce sera moyenneA > moyenneB ou moyenneA < moyenneB.
- Un test bilatéral est un test statistique où le paramètre de l’hypothèse alternative sera différent, sans un signe connu (moyenneA ≠ moyenneB ).
Dans notre exemple, notre hypothèse alternative est H1 : « le rythme cardiaque est plus faible après qu’avant le don du sang ». Cela correspond à un test unilatéral. Si l’hypothèse alternative était H1 : « le rythme cardiaque est différent avant et après le don du sang » alors ce serait un test bilatéral.
Sur python, on utilise le module stats de la librairie scipy pour l’ensemble des tests statistiques.
L’ensemble des fonctions de tests statistiques ont l’argument alternative pour spécifier le type:
- alternative = {« greater »} / {« less »} pour un test unilatéral,
- alternative= {« two-sided »} pour un test bilatéral (par défaut si rien n’est précisé).
4eme étape : Choix du test adapté
C’est une étape très importante, car un mauvais choix de test peut conduire à des erreurs d’interprétation des résultats.
Il y a plusieurs critères à prendre en compte concernant ce choix notamment :
- la taille de l’échantillon,
- l’indépendance entre les groupes,
- les types de variables : quantitatives/ qualitatives/ catégorielles.
Il existe aussi deux grands types de tests statistiques : les tests paramétriques et non paramétriques.
Les tests paramétriques sont des tests dont l’échantillon que nous étudions suit une certaine loi (loi normale par exemple) ou vérifie un certain nombre d’hypothèses (même variance entre les deux échantillons donnés). Ils sont plus puissants mais nécessitent un certain nombre d’hypothèses à vérifier.
Si l’échantillon que nous avons à disposition ne vérifie pas les hypothèses données, alors on applique un test non paramétrique. Ce sont des tests plus robustes et valides dans beaucoup de situations.
Attention, même si les tests statistiques non paramétriques sont plus robustes et peuvent donc être utilisés dans un plus grand nombre de situations, ils ont quand même des conditions de validité à vérifier.
Cette étape est nécessaire pour ne pas conclure à une hypothèse fausse au final !
Dans notre exemple on a peu de données, qui sont indépendantes les unes des autres (les individus qui ont donné leur sang ont été choisis aléatoirement dans la base de données). On choisit donc d’appliquer le test non paramétrique des rangs signés de Wilcoxon.
5ème étape : Analyse des résultats
Après le choix du test et son exécution, on obtient en sortie plusieurs données et notamment la p-value. C’est ce qui va nous permettre de répondre au test. La p-value est le niveau à partir duquel on se met à rejeter Ho.
Si p-value < alpha, alors on rejette Ho au niveau alpha,
Si p-value > alpha, alors on conserve Ho au niveau alpha.
Plus la p-value observée est faible, plus on a envie de rejeter Ho car cela veut dire que la valeur de la statistique utilisée pour le test est atypique pour Ho.
Attention ! La p-value n’est pas la probabilité que l’hypothèse de test soit vraie. La p-value indique dans quelle mesure les données sont conformes à l’hypothèse de test et à ses hypothèses. (Source wikipédia)
Ainsi on peut à présent rejeter ou conserver l’hypothèse nulle et donc conclure notre test. Dans notre exemple on obtient une p-value de 0.039 < 0.05, alors on rejette Ho au niveau alpha = 0.05 donc « le rythme cardiaque est plus faible après qu’avant le don du sang ».
Un test statistique permet de prendre une décision entre deux hypothèses. Avant de partir tête baissée et d’appliquer une fonction qui va nous donner le résultat, il est important de poser le problème étape par étape. La formulation des hypothèses, le choix du test statistique et l’analyse des résultats sont les étapes les plus importantes. Si vous souhaitez en savoir plus sur les tests statistiques un module y est consacré dans notre formation de Data Analyst et de Data Scientist.










