La notion de dérivée est notamment très utilsée en DataScience pour l’apprentissage des modèles de machine learning. En dehors de ce que vous avez pu sûrement voir au lycée, les applications de cet outil mathématiques sont bien plus vastes et nous y reviendrons à la fin de cet article. Dans cet article, vous apprendrez d’abord comment calculer la dérivée d’une fonction puis nous verrons en peu plus en détail l’utilité de ce calcul.
Définition
La dérivée d’une fonction f(x) représente le taux de variation de cette fonction. Elle peut être dénotée f’(x) ou encore dfdx. Le calcul et l’étude de la dérivée sont des notions importantes dans l’étude des fonctions.
Formules
Le calcul d’une dérivée est en général assez simple si l’on connaît les formules de base des fonctions usuelles.
Ces formules sont récapitulées dans le tableau ci-dessous :
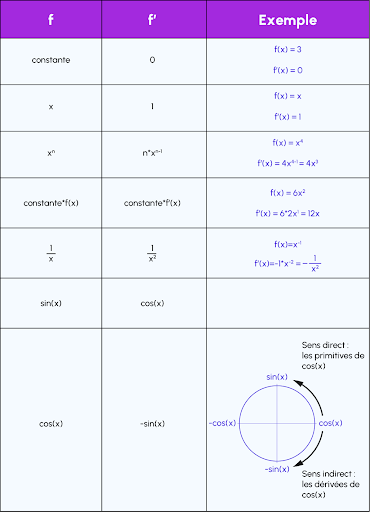
Ce tableau vous permet d’avoir les dérivées les plus basiques.
Somme de fonctions
Si votre fonction est la somme de plusieurs autres fonctions :
f(x)=u(x)+v(x)
alors sa dérivée sera la somme des dérivées:
f'(x)=u'(x)+v'(x)
Par exemple:
f(x)=x2+3
Dans ce cas u(x)=x2 et v(x)=3
Nous pouvons donc calculer
u'(x)=(x2)’=2x2-1=2x
v'(x)=(3)’ = 0
f'(x)=u'(x)+v'(x) = 2x + 0 = 2x
Produits de fonctions
Pour les multiplication de fonctions:
f(x)=u(x)*v(x)
La dérivée totale est un peu plus particulière et répond à la règle suivante:
f'(x)=u'(x)*v(x)+u(x)*v'(x)
f(x)=x2sin(x)
Dans ce cas u(x)=x2 et v(x)=sin(x)
Nous pouvons donc calculer
u'(x)=(x2)’=2x2-1=2x
v'(x)=(sin(x))’ = cos(x)
f'(x)=u'(x)*v(x)+u(x)*v'(x) = 2x*sin(x) + x2*cos(x)
Quotients de fonctions
A présent si une fonction et la division de deux autres fonctions: f(x)=u(x)v(x) alors la dérivée sera
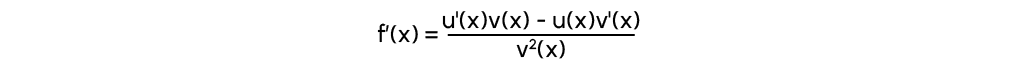
Exemple :
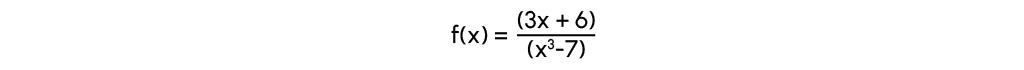
Dans ce cas u(x)=(3x+6) et v(x)=(x3-7)
Nous pouvons donc calculer
u'(x)=(3x+6)’=3
v'(x)=(x3-7)’ =3x2
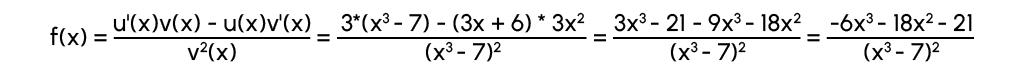
Fonctions composées
Si votre fonction est perçue comme deux fonctions regroupées, ou en d’autres termes, fonction d’une fonction :
h(x)=f(g(x))=f ◦ g
alors sa dérivée de calculée de la sorte:
h'(x)=(f ◦ g) ‘ = g’ .(f ‘ ◦ g)
Par exemple :

On peut donc considérer :
g(x)=x2+2x-4 et g'(x)=2x+2
f(x)=x et f'(x)=121x1/2=12x

Et

Et donc

Applications
Mais à quoi sert vraiment le calcul de la dérivée ?
Pour faire simple, le signe de la dérivée permet d’indiquer les variations de la fonction f. C’est ce qui représente la tangente à la fonction. Et la dérivée elle-même représente le coefficient directeur de la tangente à f au point.
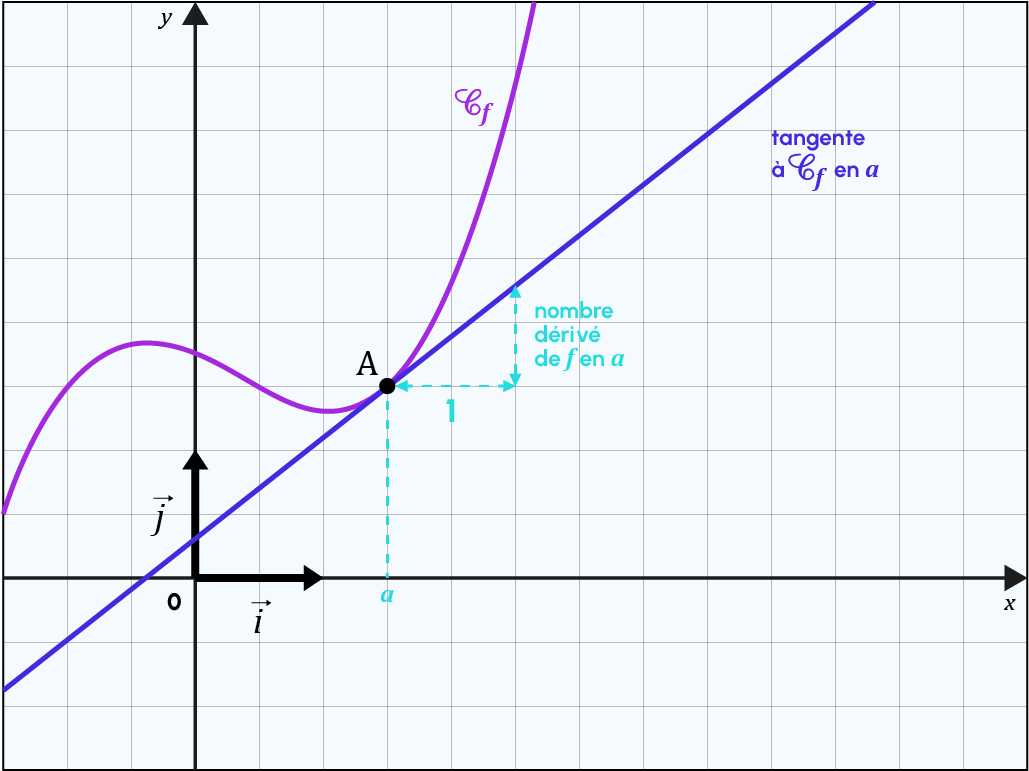
Rappel : La tangente d’une fonction en un point est la droite qui touche la fonction en ce point, et uniquement ce point.
Si f ‘ ≥ 0, alors f est croissante
Si f ‘ ≤ 0, alors f est décroissante
Et lorsque f’=0, nous avons le point x pour lequel le coefficient directeur de la tangente s’annule et la fonction f change possiblement de variation.
Par exemple:
f(x)=x2-4x+2
f'(x)=2x-4
f'(x)=0 ⇔ 2x=4 ⇔ x=2
Cela indique donc que pourx=2, ma fonction change peut-être de variation. En effet comme on peut le voir ci-dessous, x=2 constitue un point d’inflexion :

Ainsi, en remplaçant x par x<2 par exemple x=1,
Nous avons:
f'(1)=2 × 1-4=⎯2<0
La dérivée est inférieure à 0 donc la fonction f décroît.
En remplaçant x par x>2 par exemple x=3,
Nous avons :
f'(3)=2*3-4=2>0
La dérivée est supérieure à 0 donc la fonction f croît.
Nous avons donc le tableau de variation suivant:
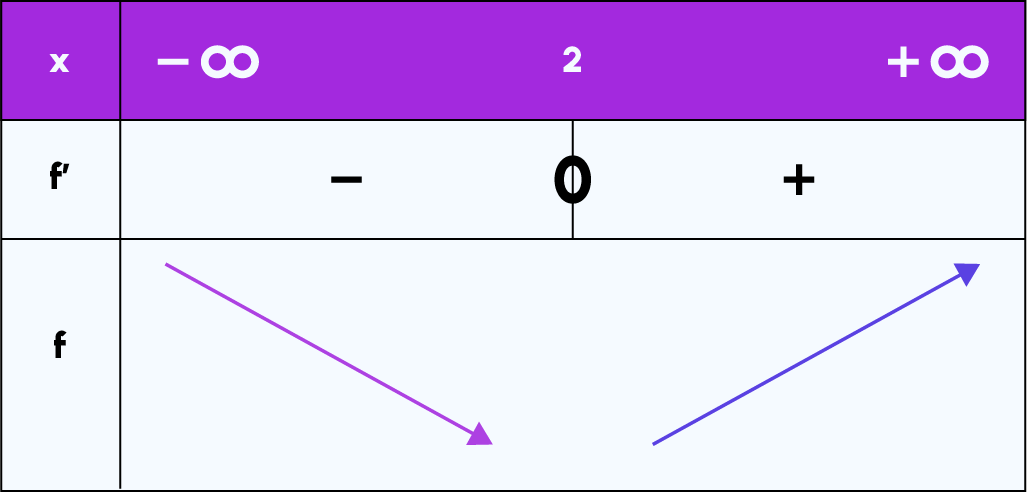
Mais alors quel est le lien avec le Machine Learning ?
Dans les problèmes de machine learning, nous cherchons à trouver le minimum de la fonction de coût afin de minimiser l’erreur de la prédiction et ainsi maximiser les performances du modèle.
Pour ce faire, nous allons chercher le minimum de la fonction grâce à la dérivée.
Cependant, le calcul de la dérivée et son égalité à 0 afin de trouver les x correspondants, ne permet pas de trouver de manière certaine des solutions analytiques.
C’est pour cette raison que nous utilisons la méthode de descente de gradient. Pour en savoir plus sur cette technique, vous pouvez consulter cet article.










