"Tu prends la pilule bleue, l'histoire s'arrête là, tu te réveilles dans ton lit, et tu crois ce que tu veux. Tu prends la pilule rouge, tu restes au Pays des Merveilles et je te montre jusqu'où va le terrier." Connaître la vérité ou rester dans son confort, découvrir la matrice ou n’en rester qu’un objet.
Ce choix cornélien du film Matrix aura fait rêver des générations entières et la matrice est devenue une icône légendaire de la pop culture, elle est rentrée dans le vocabulaire commun. Cependant, avant d’être un système développé par des machines pour exploiter des individus telles des batteries jetables, les matrices sont des outils mathématiques puissants à l’importance considérable dans de nombreux domaines, de l’algèbre linéaire aux probabilités en passant par les modèles markoviens ou la résolution de systèmes d’équations. Nous allons dans cet article présenter cet outil et en voir les premières propriétés, ainsi que les manières de les implémenter en Python.
Qu’est-ce qu’une matrice ?
En mathématique, une matrice correspond à un tableau d’éléments. Il est défini par sa dimension (le nombre de lignes et de colonnes) et par les différents éléments présents dans ce dernier.
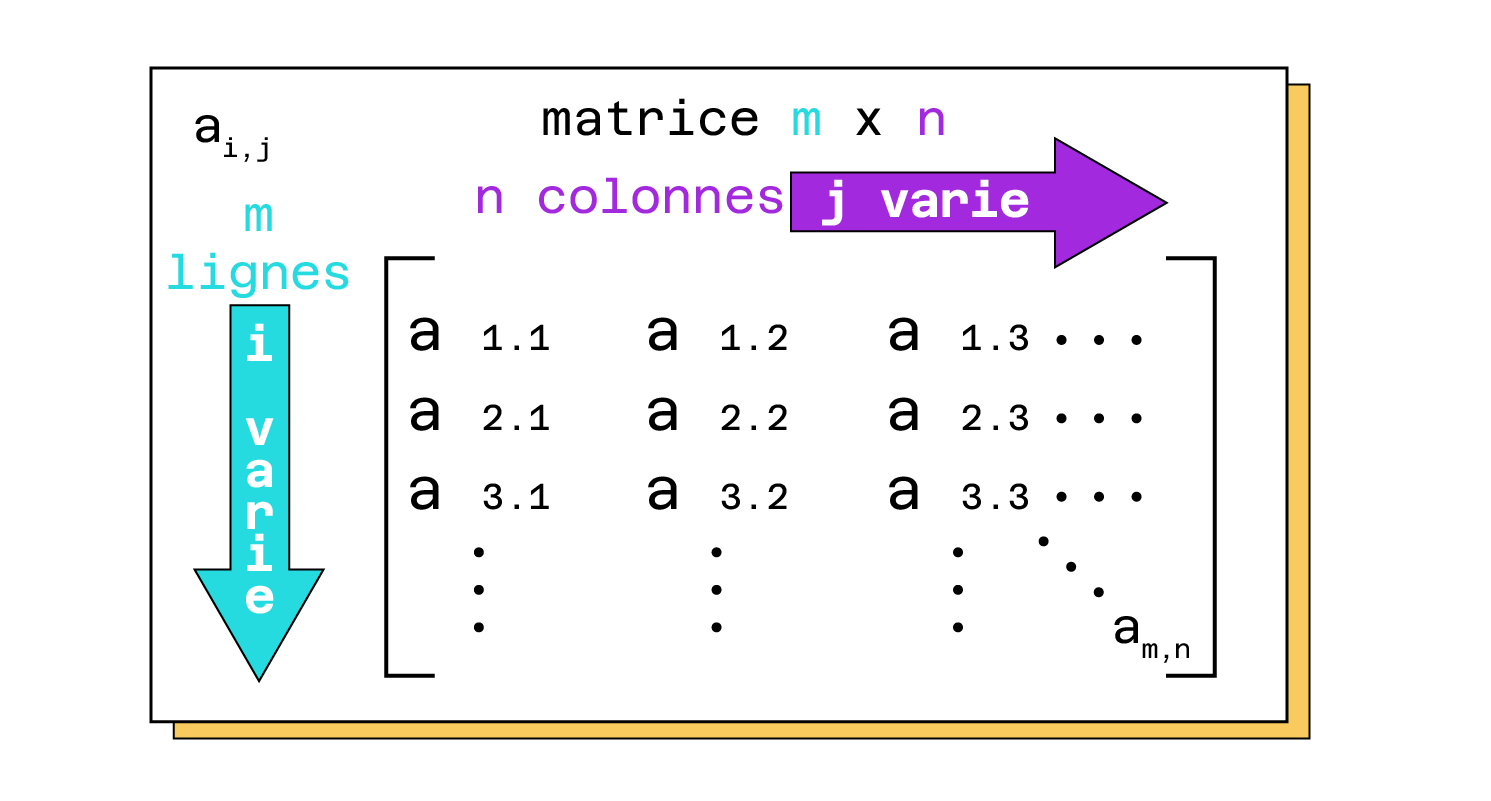
Dans cette matrice, n correspond au nombre de colonnes, m correspond au nombre de lignes, i et j sont les indices qui permettent de retrouver un élément (à la manière des coordonnées).
Les différentes matrices usuelles
- Une matrice ne comportant que des éléments vides est appelée la matrice nulle.
- Lorsqu’il y a le même nombre de lignes que de colonnes, on parle de matrice carrée
- Une matrice carrée n’ayant que des éléments nuls sauf sur la diagonale est appelée matrice diagonale
- Une matrice diagonale ne comportant que des 1 sur la diagonale est appelée la matrice identité
- Une matrice carrée ne comportant que des éléments sous la diagonale est appelée matrice triangulaire inférieure
- Une matrice carrée ne comportant que des éléments au-dessus de la diagonale est appelée matrice triangulaire supérieure
Les opérations sur les matrices
Il existe de nombreuses opérations que nous pouvons effectuer sur les matrices ou entre elles, nous donnant de nouvelles matrices. Les plus courantes sont les suivantes
- La transposition : La transposition correspond à la transformation qui transforme les lignes en colonne et inversement, à la manière d’un miroir.

- L’addition : l’addition entre matrices de même dimension revient à additionner chacun des éléments des matrices.
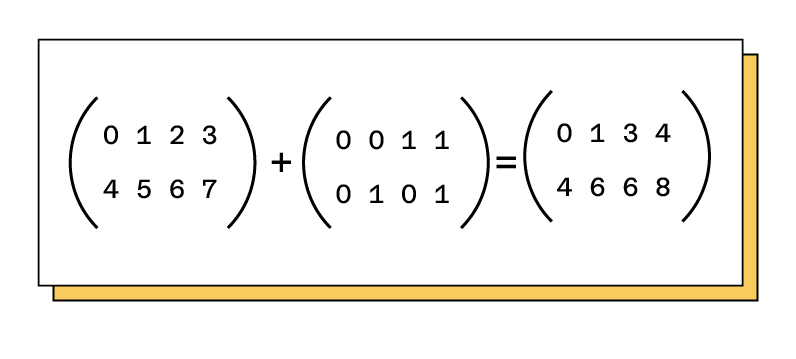
- La multiplication par un scalaire : Multiplier une matrice par un scalaire correspond à la multiplication de chacun des éléments par ce scalaire (multiplier par k revient à additionner k fois les éléments entre eux).
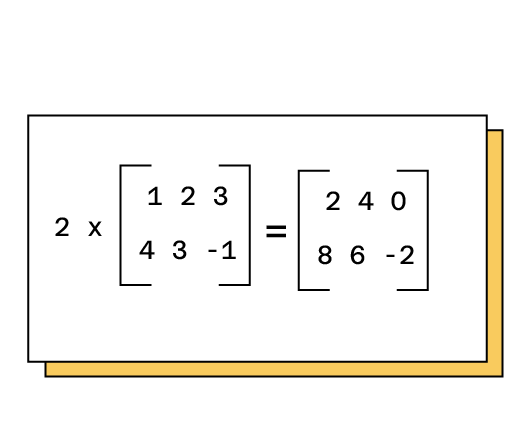
- Le produit matriciel : Le produit d’une matrice ligne avec une matrice colonne est défini de la manière suivante :
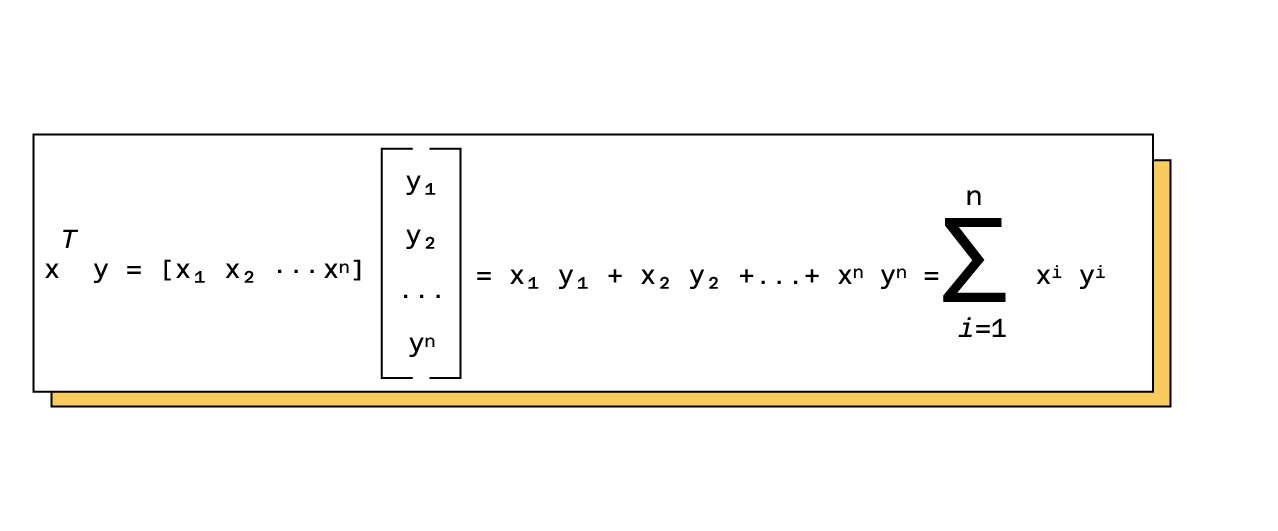
À partir de cette définition, nous pouvons définir le produit matriciel entre deux matrices. Chaque élément d’indice i,j de la matrice produit correspond au produit de la i-ème ligne et de la j-ème colonne. Par exemple :
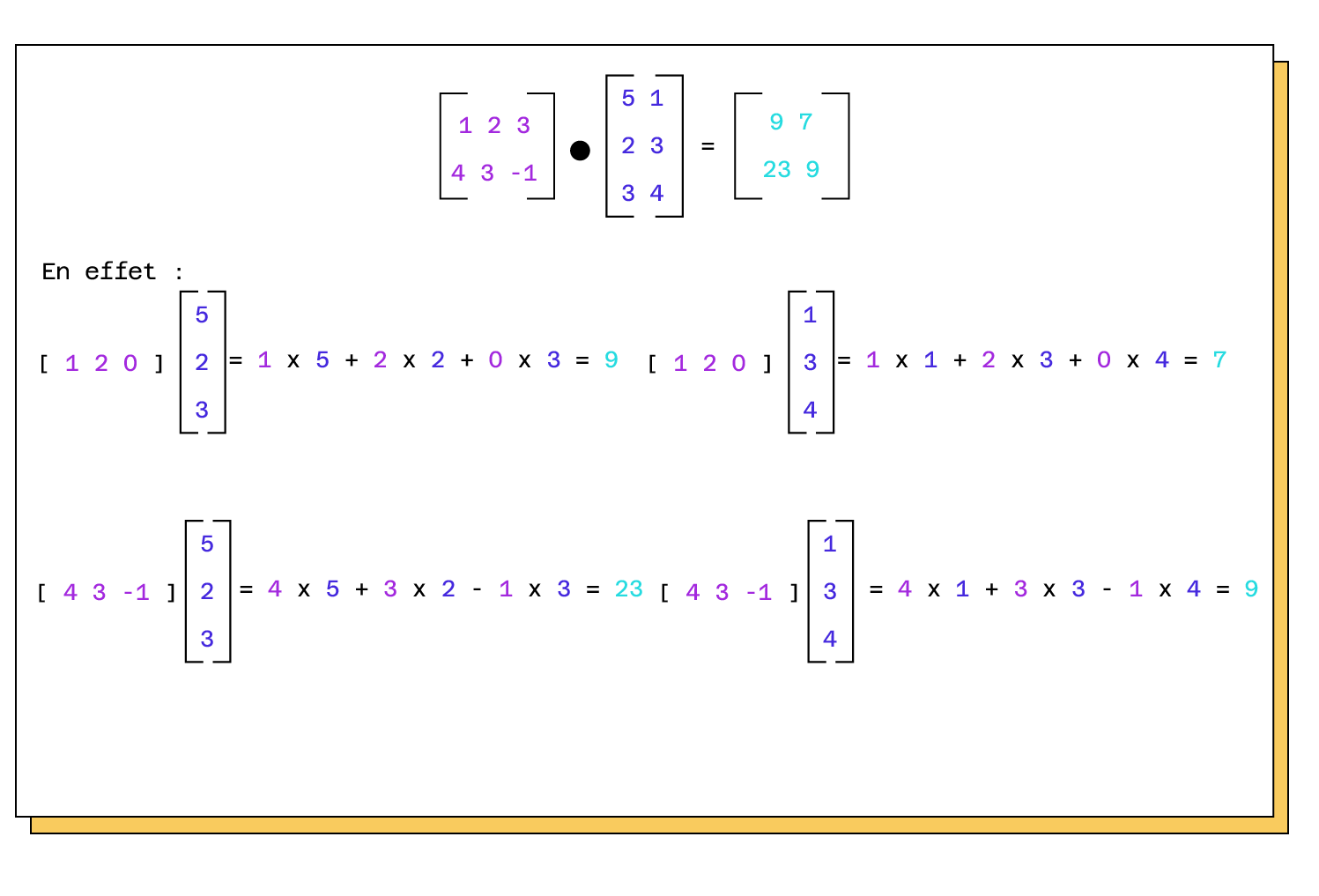
Attention : Il faut que la première matrice ait le même nombre de lignes que la deuxième en a de colonne et inversement pour que le produit fonctionne bien.
Propriétés du produit matriciel
- Le produit matriciel est :
- associatif : ABC = (AB)C = A(BC)
- distributif par rapport à l’addition : A(B + C) = AB + AC
- non commutatif : AB n’est pas égal à BA en général.
- La matrice unité I est élément neutre pour la multiplication : AIm = InA = A, si la matrice A est de dimensions n × m.
- Transposée d’un produit : (AB)T = BTAT (Attention au changement d’ordre !).
- Inverse d’une matrice : Pour une matrice carrée A, s’il existe une matrice B tel que AB vaut l’identité, alors BA vaut également l’identité, B est unique et s’appelle l’inverse de A. Plus généralement, l’inverse d’une matrice A se note A-1 .
Implémentation en Python
Pour implémenter des matrices en Python, on peut passer par des listes à deux dimensions ou des tableaux Numpy. Voici un script présentant des exemples d’utilisation :
Les matrices n’ont dorénavant aucun secret pour vous, vous avez toutes les cartes en main pour comprendre ces objets qui sont bien plus puissants que Neo ou Morpheus.










