Le codage de Huffman est un algorithme de compression de données. L’idée est d’affecter des codes de longueur variable aux caractères d’entrée, la longueur des codes assignés étant basée sur la fréquence d’apparition des caractères dans la séquence initiale.
Le codage de Huffman est un algorithme de compression des données sans perte. Cet algorithme a été inventé en 1952 par David Albert Huffman. Le codage de Huffman est généralement important pour compresser des données dans lesquelles il y’a des caractères qui apparaissent fréquemment. Le facteur fréquence est pris en compte dans ce cadre à cause de la notion d’entropie de l’information, car plus un caractère est fréquent, plus l’entropie de ce caractère est élevée.
Comment le codage de Huffman fonctionne-t-il ?
Le principe du codage de Huffman repose sur la construction d’une structure d’arbre avec des nœuds.
Dans cet algorithme, on se base sur l’idée selon laquelle la meilleure manière de coder une information est de trouver la longueur optimale pour représenter chaque caractère de la séquence initiale. La longueur optimale du code correspondant à un caractère est donnée par le nombre de branches qu’il faudra parcourir partant du sommet de l’arbre de Huffman ou Huffman Tree en anglais pour arriver à ce caractère qui sera toujours une feuille de la Huffman Tree.
L’idée derrière l’arbre de Huffman est de minimiser la longueur des symboles qu’on utilise pour coder un message et ceci revient en quelque sorte à minimiser la taille de cet arbre. On pourrait cependant se demander comment s’effectue la construction de l’arbre de Huffman.
C’est quoi le principe du codage de Huffman ?
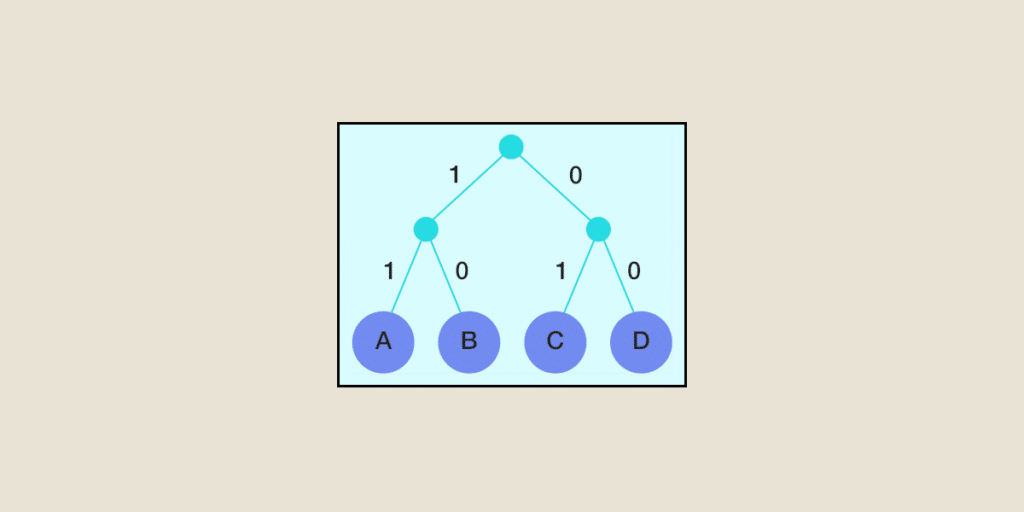
Pour ce qui est de la construction de l’arbre, on associe chaque fois les deux nœuds de plus faibles poids, pour donner un nouveau nœud « père » dont le poids est équivalent à la somme des poids de ses fils. On réitère ce processus jusqu’à n’en avoir plus qu’un seul nœud : la racine de l’arbre de Huffman qui aura pour poids la somme des poids de tous les nœuds feuilles initiaux. On associe ensuite par exemple le code 0 à chaque embranchement partant vers la gauche et le code 1 vers la droite. Pour obtenir le code binaire de chaque caractère, on effectue un parcours de l’arbre allant du sommet jusqu’aux feuilles en prenant à chaque fois le caractère 0 ou 1 des branches que l’on traverse selon qu’on passe par la droite ou par la gauche.
Les différentes étapes de la construction de la Huffman Tree
- Construire des nœuds feuilles à partir de chaque caractère du message à coder, chaque caractère étant pris en compte une seule fois avec les différentes fréquences d’apparition des caractères à ranger par ordre de priorité, les prioritaires étant ceux de plus faibles fréquences.
- Extraire les deux noeuds de plus faibles poids par ordre croissant de fréquence c’est-à-dire le noeud ayant la fréquence la plus faible doit être extrait en premier.
- Créer un nouveau nœud interne avec une fréquence égale à la somme des fréquences de ces deux nœuds. Définir le premier nœud extrait comme le fils gauche de ce nœud et le second nœud comme le fils droit. Ajouter le nouveau noeud créé à la liste des autres noeuds restants.
- Répéter les étapes 2 et 3 jusqu’à être passé(e) par tous les nœuds obtenus à l’étape 1. Le nœud restant est la racine de l’arbre et la construction est terminée.
Un exemple pour illustrer le codage
Pour illustrer l’idée du codage de Huffman, nous allons considérer le message ci-dessous que nous allons représenter de manière optimale sous forme binaire:
aabbccddbbeaebdddfffdbffddabbbbbcdefaabbcccccaabbddfffdcecc
Pour un message à coder comme celui-ci, commençons d’abord par comptabiliser la fréquence des caractères distincts dans le message. Après comptabilisation, on obtient le résultat suivant :
a:8, b:15, c:11, d:12, e:4, f:9
Nous allons implémenter l’algorithme du codage de Huffman sur cet exemple.
La première étape consiste à utiliser les caractères les moins fréquents dans le message à coder. Il faudra donc commencer avec les lettres ‘e’ et ‘a’ qui ont les fréquences les plus faibles, puis sommer leurs poids c’est-à-dire sommer leurs fréquences d’apparition afin de remplacer les deux caractères par un nouveau caractère unique qui aura pour fréquence la somme des fréquences de ces deux caractères dans la liste. Au terme de cette première étape, la liste devient :
new node:12, b:15, c:11, d:12, f:9
où le nœud new node remplace les nœuds a et e avec un poids égal à la somme de leurs poids respectifs. [ new node : 12 = (a:8, e:4)]
Ensuite, il faudra choisir dans la nouvelle liste obtenue les deux éléments ayant les plus petits poids, puis itérer le processus jusqu’à obtenir le nœud de poids maximal c’est-à-dire ayant pour poids la somme des fréquences de tous les caractères. On remarque qu’à la fin de la construction de l’arbre de Huffman, tous les caractères distincts du message initial à coder sont des feuilles de l’arbre de Huffman, encore appelés Leaf Nodes en anglais. On obtient les résultats ci-dessous au terme de l’exécution :
d -> 00
e -> 010
a -> 011
b -> 10
f -> 110
c -> 111
On rappelle que les étiquettes de l’arbre de Huffman sont marquées en prenant la convention de mettre un 0 sur l’étiquette de gauche et un 1 sur l’étiquette de droite dans l’ordre descendant c’est-à-dire de la racine de l’arbre aux feuilles.
La complexité temporelle de cet algorithme est quasi-linéaire c’est-à-dire en O(nlogn) où n est le nombre de caractères uniques de la liste à compresser et la complexité spatiale est linéaire donc en O(n).
À quoi sert le codage de Huffman dans la vie active ?
En ce qui concerne les différentes applications de l’algorithme du codage de Huffman pour la compression de données, nous pouvons citer la transmission des fax et des textes, les formats de compression conventionnelle comme GZIP, les logiciels multimédia comme JPEG, PNG et MP3.
En général, la compression des données est utile pour augmenter les capacités de stockage en mémoire ou la vitesse de transmission des données.
Il existe des variantes du codage de Huffman lors de la création de l’arbre.
- Soit le dictionnaire est statique : chaque caractère a un code prédéfini et connu ou publié à l’avance (il n’a donc pas besoin d’être transmis) ;
- Soit le dictionnaire est semi-adaptatif : le contenu est analysé pour calculer les fréquences de chaque caractère et un arbre optimisé est utilisé pour le codage (il doit alors être transmis pour le décodage) ;
- Soit le dictionnaire est adaptatif : à partir d’un arbre connu (publié avant et donc non transmis) celui-ci est modifié pendant la compression et optimisé au fur et à mesure. Le temps de calcul est beaucoup plus long mais propose souvent un meilleur taux de compression.
En définitive, le codage de Huffman est un algorithme de compression de données très utile qui a plusieurs applications de nos jours, de l’augmentation de la capacité de stockage à l’augmentation de la vitesse de transmission des données. On peut retrouver cette technique de compression de données sous plusieurs variantes parmi lesquelles la variante dynamique qui est une amélioration de la variante statique dont le principe a été présenté dans cet article.