Connue également sous le nom de recherche par moitié, la recherche dichotomique est un algorithme puissant dans le domaine de l’informatique et l’algorithmique qui permet de trouver rapidement une valeur dans un ensemble de données triées. Accrochez-vous pour découvrir en profondeur son fonctionnement, ses avantages et ses inconvénients ainsi que ses applications.
Les origines de la recherche dichtomique
Les origines de la recherche dichotomique se retrouvent dans les travaux mathématiques antiques : les bases de cette méthode ont été établies, comme pour la plupart des choses, dès l’Antiquité par des penseurs grecs, notamment le célèbre philosophe et mathématicien Euclide qui a vécu vers 300 avant notre ère.
En tant qu’algorithme de recherche efficace, la recherche dichotomique a été développée plus tard, au XXe siècle, avec l’arrivée de l’informatique et l’algorithmique. La toute première allusion à cette méthode est souvent attribuée à l’informaticien américain John W. Mauchy en 1946 dans ses Moore School Lectures. Mauchy est aussi reconnu pour avoir développé le premier ordinateur électronique à grande échelle, l’ENIAC (Electronic Numerical Integrator and Computer) avec J. Presper Eckert.
La recherche dichotomique a ensuite été formalisée et popularisée par Donald Knuth dans son ouvrage The art of Computer Programming (L’art de la programmation informatique). Les premières éditions de cet ouvrage, publiées dans les années 1960, ont grandement contribué à l’établissement de la recherche dichotomique comme technique d’exploration de données fondamentale, largement utilisée dans le domaine de l’informatique.
Aujourd’hui, la conception élégante et sa performance supérieure par rapport à d’autres méthodes de recherche ont fait de la recherche dichotomique une technique incontournable pour de nombreuses applications informatiques et scientifiques.

Comment cela fonctionne ?
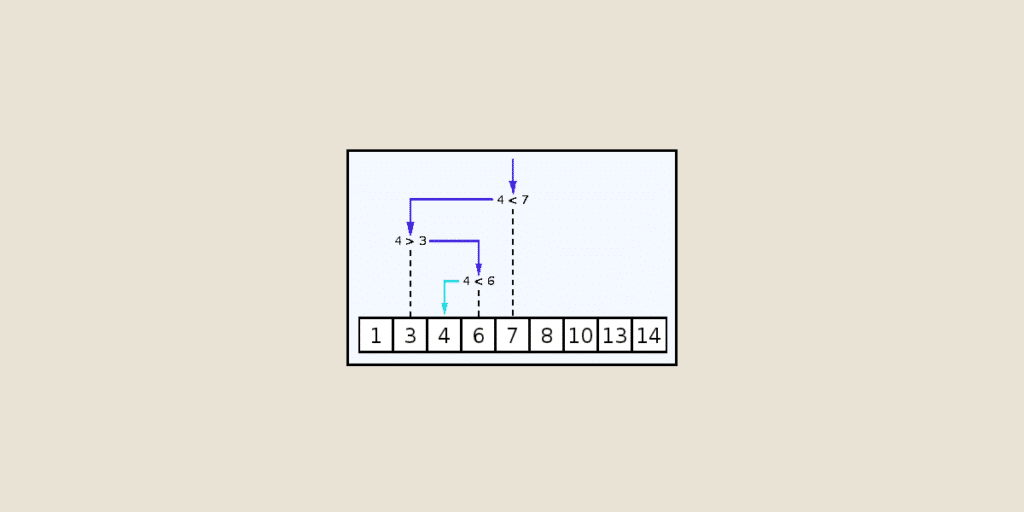
De façon générale, la recherche dichotomique s’applique à un tableau trié en divisant continuellement l’intervalle de recherche en deux de sorte que l’espace de recherche se réduit à chaque itération. Ainsi, cette méthode a une performance bien meilleure que celle de la recherche linéaire, en particulier lorsque les volumes des données sont importants.
Pour garantir le bon fonctionnement de la recherche binaire, il est importante de vérifier les conditions suivantes:
- Données triées: La recherche binaire ne peut être utilisée que sur un ensemble de données triées, que ce soit dans l’ordre croissant ou décroissant.
- Structure indexable: L’implémentation est plus facile lorsqu’il s’agit des structures de données indexables, telles que les tableaux ou les listes chaînées avec accès direct aux éléments par index.
- Taille statique: Si le tableau est fréquemment modifié, la recherche binaire pourrait devenir moins avantageuse car il faudrait réajuster le tableau à chaque modification.
- Comparabilité des éléments: Des opérations de comparaison comme « plus petit que », « plus grand que » ou « égal que » peuvent être établies entre les éléments.
Pour commencer, parcourons les étapes de cette méthode avec un exemple. Après ceci on donnera un code pour son implémentation itérative et récursive.
1. Considérons le tableau suivant :
𝑎𝑟𝑟𝑎𝑦 = [2, 8, 13, 28, 45, 56, 79, 84, 95, 102]
Et supposons que l’on cherche l’élément 𝑥 = 79.
2. On initialise deux pointeurs avec l’index première et la dernière position de notre tableau, dans notre cas on aura 𝑙𝑜𝑤 = 0 et ℎ𝑖𝑔ℎ = 9.
3. On calcule l’index qui se trouve au milieu et on compare son élément à 𝑥 = 79. Si notre 𝑥 est égal à l’élément au milieu on aura terminé. Si 𝑥 est plus petit, on déplace le champ de recherche vers la gauche, sinon on le déplace vers la droite.
De sorte que pour notre exemple on a dans un premier temps :
𝑥 = 79
𝑙𝑜𝑤 = 0
ℎ𝑖𝑔ℎ = 9
𝑚𝑖𝑑 = 4
𝑎𝑟𝑟𝑎𝑦[𝑚𝑖𝑑] = 45
Comme 𝑎𝑟𝑟𝑎𝑦[𝑚𝑖𝑑] = 45 < 79 = 𝑥, on déplace le champ de recherche vers la droite et on réinitialise le pointeur 𝑙𝑜𝑤 comme: 𝑙𝑜𝑤 = 𝑚𝑖𝑑 + 1. Le pointeur high reste pareil.
Notre champ de recherche est désormais délimité par les chiffres en bleue:
𝑎𝑟𝑟𝑎𝑦 = [2, 8, 13, 28, 45, 56, 79, 84, 95, 102]
4. On répète la 3ème étape de sorte qu’on a :
𝑥 = 79
𝑙𝑜𝑤 = 5
ℎ𝑖𝑔ℎ = 9
𝑚𝑖𝑑 = 7
𝑎𝑟𝑟𝑎𝑦[𝑚𝑖𝑑] = 84
Comme 𝑎𝑟𝑟𝑎𝑦[𝑚𝑖𝑑] = 84 > 79 = 𝑥, on déplace le champ de recherche vers la gauche et réinitialise le pointeur high comme: ℎ𝑖𝑔ℎ = 𝑚𝑖𝑑 – 1. Le pointeur 𝑙𝑜𝑤 reste pareil.
Notre champ de recherche est désormais :
𝑎𝑟𝑟𝑎𝑦 = [2, 8, 13, 28, 45, 56, 79, 84, 95, 102]
5. On répète la 3ème étape de sorte qu’on a :
𝑥 = 79
𝑙𝑜𝑤 = 5
ℎ𝑖𝑔ℎ = 6
𝑚𝑖𝑑 = 6
𝑎𝑟𝑟𝑎𝑦[𝑚𝑖𝑑] = 79
6. Puisque 𝑎𝑟𝑟𝑎𝑦[𝑚𝑖𝑑] = 79 = 79 = 𝑥, on a trouvé l’élément recherché et on s’arrête.
La méthode continue jusqu’à ce que l’élément est trouvé où l’espace de recherche épuisée.
Le code
Méthode itérative
Méthode récursive
Complexité algorithmique
Dans le pire des cas, la complexité de l’algorithme est de 𝑂(𝑙𝑜𝑔(𝑛)), où 𝑛 est le nombre d’éléments dans la liste, ce qui fait de la recherche dichotomique une méthode très efficace, particulièrement pour les grandes listes triées.
Avantages
- Efficacité en termes de temps : il est plus rapide que la recherche linéaire, en particulier pour les grandes listes.
- Simple à comprendre et à implémenter.
- Adaptable dans des divers contextes, tels que la recherche dans des tableaux, des listes chaînées, des arbres binaires de recherche, etc.
Limitations
- Le tableau doit être trié.
- Les éléments du tableau doivent être comparables.
Quelques applications
La recherche dichotomique est très utile lors de la création des algorithmes plus complexes utilisés en Machine Learning, par exemple dans des algorithmes d’entraînement de réseaux des neurones où pour trouver les hyperparamètres optimaux d’un modèle.
Elle peut être utilisée aussi pour faire des recherches dans une base de données volumineuse ou en graphiques informatiques comme la cartographie de textures.