Afin de mieux comprendre les données, il est primordial d’analyser leurs relations. Et pour faciliter cette analyse face à des dizaines de milliers de lignes de données, il existe des formules mathématiques. Notamment le coefficient de corrélation.
Qu'est-ce que le coefficient de corrélation ?
Relation et dépendance entre deux variables
Avant de comprendre le coefficient de corrélation, il convient de comprendre les relations entre les différentes variables d’un jeu de données. Ainsi, si les valeurs d’une variable Y dépendent de la valeur x (ou inversement), il y a une relation entre ces deux variables. La connaissance de X (ou Y) doit alors permettre de prédire l’autre variable Y (ou X).
Par exemple, la marge dégagée par une entreprise dépend (en partie) du prix de ses produits ou services. Il y a donc une corrélation entre ces deux valeurs.
En mathématique, cette relation se traduit comme suit : Y=f(X). Ici, Y est considérée comme la variable dépendante, et X est la variable indépendante.
Attention, ce n’est pas parce que X permet de déduire Y que la réciproque est avérée.
Et pour savoir s’il existe une corrélation entre deux variables, il est possible d’utiliser la formule du coefficient de corrélation. Mais avant cela, il convient de définir la forme d’une relation.
La forme de la relation entre deux variables
Pour établir la forme de la relation entre deux variables, l’outil le plus simple est la représentation graphique. Grâce à un diagramme, il est possible de croiser les modalités de X et Y, avec X en abscisse et Y en ordonnée. Ce diagramme permet alors de caractériser la relation entre les variables selon 3 paramètres :
- L’intensité : la relation entre les variables peut être forte, faible ou nulle. Elle est forte si les unités ont des valeurs voisines sur X et Y. Visuellement, cela se traduit par un nuage de points avec des valeurs rapprochées les unes des autres. À l’inverse, si les valeurs voisines de X sont éloignées de Y, la relation est faible. Et si elles sont très éloignées (sans aucune ligne directrice), la relation est nulle. Autrement dit, il n’est pas possible de prédire Y grâce à X.
- La forme : la relation peut être linéaire et monotone (une ligne droite sur le graphique, non linéaire et monotone (une courbe strictement croissante ou décroissante) ou non linéaire et non monotone (la courbe sera à la fois croissante et décroissante, comme une parabole ou une hyperbole).
- Le sens : cela s’applique aux relations monotones. On dit alors que la corrélation est positive lorsque les deux variables vont dans le même sens, ou négative lorsqu’elles vont dans des sens opposés.
En fonction de la forme de la relation, il conviendra de sélectionner les bons outils. Et notamment la formule du coefficient de corrélation.
La formule du coefficient de corrélation
Le coefficient de corrélation est utilisé pour étudier les relations monotones (qu’elles soient linéaires ou non). Mais en fonction de leur linéarité, on utilise deux types de coefficient de corrélation (Pearson ou Spearman) que nous étudierons au prochain paragraphe.
La formule utilisée diffère alors selon le type de relation. Mais elle s’écrit toujours sous cette forme « r« .
Le coefficient de corrélation peut être utilisé pour faire le lien entre une multitude de variables. Par exemple, la relation entre la taille et l’intelligence, le prix et les marges, le nombre d’habitants et la pollution, les apports caloriques et la maladie, etc.
Quels sont les différents coefficients de corrélation ?
Le coefficient de corrélation de Pearson
Il s’agit alors d’étudier les relations linéaires et monotones.
La formule du coefficient de corrélation de Pearson se présente comme suit :
Pour calculer le coefficient de corrélation de Pearson, il convient donc de commencer par calculer la covariance. C’est-à-dire, la moyenne du produit des écarts à la moyenne.
Ensuite, il suffit de diviser cette covariance par le produit des écarts-types de X et Y.
En fonction du résultat, vous pourrez interpréter la relation entre les deux variables. Ainsi :
- si r est proche de 0 : la relation linéaire est nulle. Attention, ce n’est pas parce qu’il n’y a pas de relation linéaire entre deux variables qu’il n’y a pas de relation du tout.
- si r est proche de -1 : il y a une forte relation linéaire les deux variables, mais négative. Elles vont donc dans des sens opposés.
- si r est proche de 1 : il y a une forte relation linéaire positive entre les deux variables. Elles vont dans le même sens.
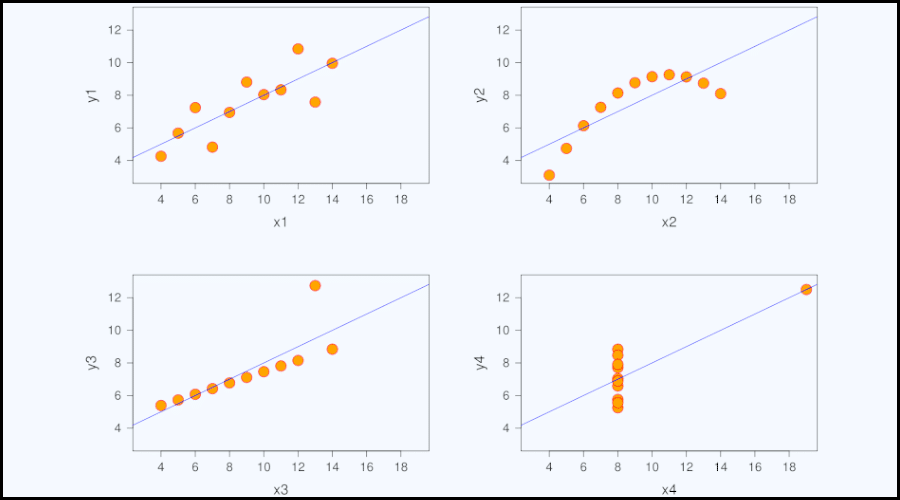
Bon à savoir : si cette formule du coefficient de corrélation est efficace pour mieux comprendre la relation entre deux variables, cela ne fonctionne que si la distribution ne présente pas de valeurs aberrantes. À défaut, les résultats du calcul peuvent aboutir à des conclusions totalement erronées.
Le coefficient de corrélation de Spearman
Cette formule (également appelé coefficient de corrélation de rang) permet d’analyser les relations monotones. Et ce, quelle que soit la forme de la relation (linéaire, exponentielle, ….). À ce titre, le coefficient de Spearman s’adapte mieux lorsqu’il y a des valeurs aberrantes ou des distributions dissymétriques. À travers ce calcul, ces dernières risquent moins de fausser le résultat.
Quelles sont les limites du coefficient de corrélation ?
La formule du coefficient de corrélation n’est que la première étape dans la détermination des relations entre plusieurs variables. Pour avoir une vision plus globale, il est primordial de réaliser d’autres calculs mathématiques, comme le test de significativité et la vérification de l’absence de biais.
Utilisés ensemble, ces différents outils statistiques vous permettent de faire quelques pas supplémentaires dans la constitution d’un modèle d’apprentissage automatique. Mais pour mieux comprendre les connexions entre les données et les réseaux neuronaux, mieux vaut se former complètement à la science de la donnée. Pour cela,rejoignez la formation Datascientest.
Ce qu’il faut retenir
- Le coefficient de corrélation permet d’indiquer les relations entre plusieurs variables.
- Il donne ainsi une indication concernant l’intensité, la forme et le sens de la relation.
- Selon le type de relation, il est possible d’utiliser les coefficients de corrélation de Spearman ou de Pearson.