Comment gérer les problèmes de Classification déséquilibrée ?
Partie I
La classification sur données déséquilibrées est un problème de classification où l’échantillon d’apprentissage contient une forte disparité entre les classes à prédire. Ce problème revient fréquemment dans les problèmes de classification binaire, et notamment la détection d’anomalies.
Cet article sera divisé en deux parties : La première s’intéresse au choix des métriques propres à ce type de données, la seconde détaille l’éventail de méthodes utiles pour obtenir un modèle performant.
Partie I : Le choix des bonnes métriques
Qu’est ce qu’une métrique d’évaluation ?
Une métrique d’évaluation quantifie la performance d’un modèle prédictif.
Le choix de la bonne métrique est donc crucial lors de l’évaluation des modèles de Machine Learning, et la qualité d’un modèle de classification dépend directement de la métrique utilisée pour l’évaluer.
Pour les problèmes de classification, les métriques consistent globalement à comparer les classes réelles aux classes prédites par le modèle. Elles peuvent également permettre d’interpréter les probabilités prédites pour ces classes.
L’un des concepts clés de performance pour la classification est la matrice de confusion qui est une visualisation, sous forme de tableau, des prédictions du modèle par rapport aux vrais labels. Chaque ligne de la matrice de confusion représente les instances d’une classe réelles et chaque colonne représente les instances d’une classe prédite.
Prenons l’exemple d’une classification binaire, où l’on dispose de 100 instances positives et 70 instances négatives.
La matrice de confusion ci-dessous correspond aux résultats obtenus par notre modèle :
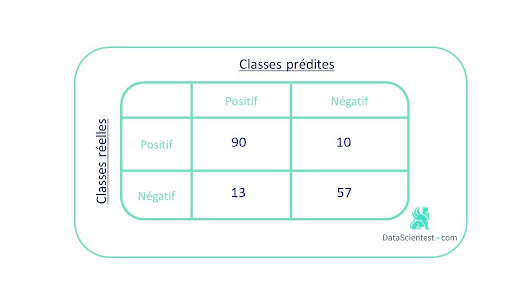
Elle permet d’obtenir une vue d’ensemble des prédictions justes et des prédictions fausse.
Pour résumer cette matrice en une métrique, il est possible d’utiliser le taux de bonnes prédictions ou accuracy . Ici il est égal à (90+57)/170 = 0.86.
Le choix d’une métrique appropriée n’est pas évident pour tout modèle de Machine Learning, mais il est particulièrement difficile pour les problèmes de classification déséquilibrée.
Dans le cas de données comportant une classe fortement majoritaire, les algorithmes classiques sont souvent biaisés car leurs fonctions de perte tentent d’optimiser des métriques telles que le taux de bonnes prédictions, en ne tenant pas compte de la distribution des données.
Dans le pire des cas, les classes minoritaires sont traitées comme des valeurs aberrantes de la classe majoritaire et l’algorithme d’apprentissage génère simplement un classifieur trivial qui classe chaque exemple dans la classe majoritaire. Le modèle semblera performant mais cela ne sera que le reflet de la surreprésentation de la classe majoritaire. On parle d’accuracy paradoxe.
Dans la majorité des cas, c’est justement la classe minoritaire qui présente le plus fort intérêt et que l’on aimerait pouvoir identifier, comme dans l’exemple de la détection de fraudes.
Le degré de déséquilibre varie mais les cas d’usages sont fréquents: dépistage de maladies, détection de panne, moteur de recherche, filtrage de spams, ciblage marketing etc…
Mise en pratique : Churn Rate
Supposons qu’une entreprise de services souhaite prédire son taux d’attrition : ‘churn rate’ en anglais.
Pour rappel le churn rate correspond au ratio : nombre de clients perdus / nombre de clients total , mesuré sur une période donnée qui est le plus souvent l’année.
Pour cela, elle souhaite prédire pour chaque client s’il résiliera son contrat à la fin de l’année.
On dispose d’un jeu de données contenant des informations personnelles et des caractéristiques relatives aux contrats de chaque client de l’entreprise pour l’année X, ainsi qu’une variable permettant de savoir s’il a renouvelé son contrat à la fin de l’année.
Dans nos données, le nombre de ‘churners’ correspond à environ 11% du nombre total de clients.
On décide d’entraîner un premier modèle de Régression logistique sur nos données préparées et normalisées.
Surprise ! Notre code affiche un taux de bonnes prédictions de 0.90 !
C’est un score très correct, mais rappelons-nous notre objectif : Réussir à prédire les départs éventuels des clients. Est-ce que ce résultat signifie que sur 10 clients « churners », 9 seront identifiés comme tels par le modèle? Absolument pas !
La seule interprétation que l’on puisse faire est que 9 clients sur 10 ont été bien classés pas le modèle.
Pour réussir à détecter le comportement naïf d’un modèle, l’outil le plus efficace est toujours la matrice de confusion.
Un premier coup d’oeil a la matrice de confusion nous indique que le bon taux de bonnes prédictions obtenu est largement influencé par le bon comportement du modèle sur la classe dominante (0).
Afin d’évaluer le modèle par rapport au comportement souhaité sur une classe, il est possible d’utiliser une série de métriques issues de la matrice de confusion, comme notamment la précision, le rappel (recall) et le f1-score, définis ci-dessous.

Ainsi pour une classe donnée:
Une précision et un rappel élevé -> La classe a été bien gérée par le modèle
Une précision élevée et un rappel faible -> La classe n’est pas bien détectée mais lorsqu’elle l’est, le modèle est très fiable.
Une précision faible et un rappel élevé -> La classe est bien détectée, mais inclut également des observations d’autres classes.
Une précision et un rappel faible -> la classe n’a pas du tout été bien gérée
Le F1-score permet de mesurer la précision et le rappel à la fois.
Dans le cas d’une classification binaire, la sensibilité et la spécificité correspondent respectivement aux rappels de la classe positive et de la classe négative.
Une autre métrique , la moyenne géométrique (G-mean) , s’avère utile pour les problèmes de classification déséquilibrée: il s’agit de la racine du produit de la sensibilité et de la spécificité.
Ces différentes métriques sont facilement accessibles grâce au package imblearn.
La fonction classification_report_imbalanced() permet d’afficher un rapport contenant notamment les résultats sur l’ensemble des métriques du package.
Nous obtenons le tableau suivant :

Le tableau montre que le rappel et le f1-score de la classe 1 sont mauvais, tandis que pour la classe 0, ils sont élevés. En outre, la moyenne géométrique est également faible.
Le modèle entraîné n’est donc pas adapté à nos données.
Dans la partie II , nous découvrirons les méthodes qui nous permettront d’obtenir de bien meilleurs résultats.
Envie d’améliorer vos compétences pour réussir à construire des modèles performants et fiables à partir d’ensembles de données déséquilibrés? Découvrez tous nos modules d’apprentissage !
N’hésitez pas à nous contacter pour plus d’infos !










