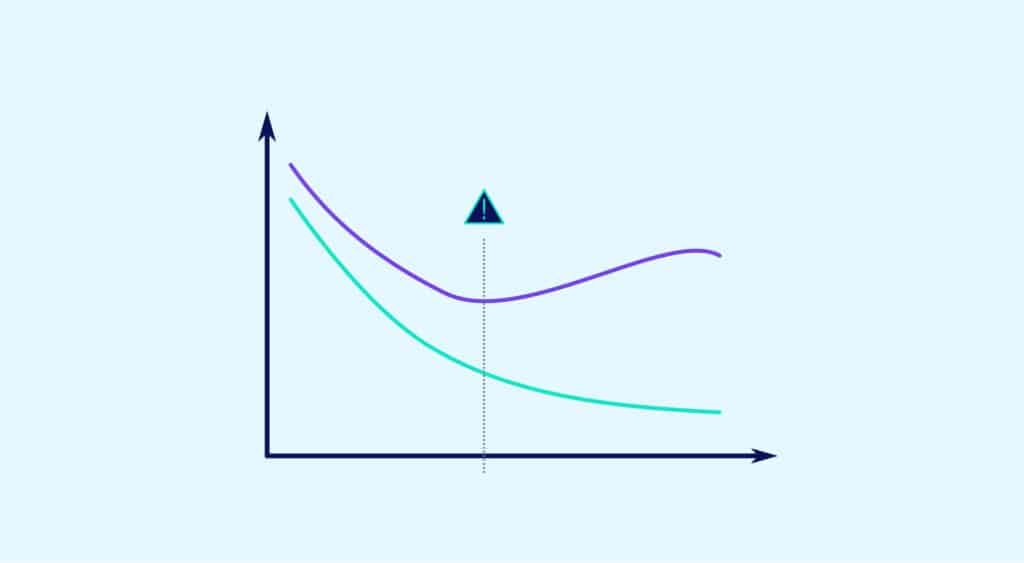
Dans cet article, nous vous présentons un des écueils des algorithmes d’apprentissage supervisé, le surapprentissage ou overfitting en anglais.
Qu’est-ce que l’overfitting?
L’overfitting est le risque pour un modèle d’apprendre “par cœur” les données d’entraînement. De cette manière, il risque de ne pas savoir généraliser à des données inconnues.
Par exemple, un modèle qui retourne l’étiquette pour les données d’entraînement et une variable aléatoire pour les données non connues aurait de très bonnes performances pendant l’entraînement, mais pas pour de nouvelles données.
Quand l'overfitting risque-t-il d’apparaître ?
L’overfitting peut arriver quand le modèle choisi est trop complexe par rapport à la taille du jeu de données.
Par exemple, le modèle choisi ici est une régression polynomiale qui se force à passer par le plus de points possibles des données d’entraînements car le degré choisi est trop important. Il délaisse ainsi de nombreux points non vus pendant l’entraînement. Sur les données d’entraînement, ce modèle a d’excellents résultats, mais sur des données non vues, l’erreur quadratique risque d’être énorme
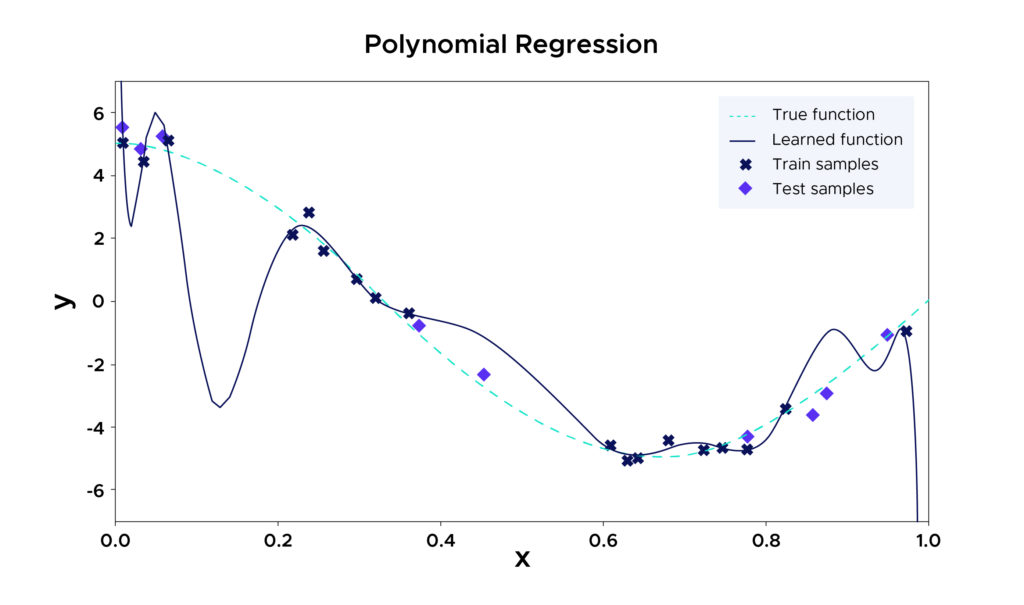
Pourquoi l'overfitting pose problème ?
À cause de l’overfitting, un modèle représente mal les données à partir desquels il a été entraîné. Son taux d’exactitude sera donc inférieur sur de nouvelles données similaires, par rapport à un modèle idéalement adapté. Pourtant, en l’appliquant aux données d’entraînement, le modèle overfitted semblera offrir une plus haute exactitude. Il est donc très facile de se laisser induire en erreur.
Sans protection contre l’overffiting, les développeurs peuvent entraîner et déployer un modèle hautement précis à première vue. En réalité, ce modèle offrira des performances amoindries en production sur de nouvelles données.
Le déploiement d’un tel modèle peut causer toutes sortes de problèmes. Par exemple, un modèle utilisé pour prédire la probabilité d’un défaut de paiement risque d’annoncer un pourcentage bien supérieur à la réalité en cas d’overfitting. Il pourra donc mener à de mauvaises décisions, provoquant un manque à gagner et l’insatisfaction des clients.
Overfitting vs Underfitting
À l’inverse de l’overfitting, l’underfitting survient quand les données d’entraînement sont hautement biaisées. Par exemple, si un problème est excessivement simplifié, le modèle ne fonctionne pas correctement sur les données d’entraînement.
Il peut être causé par des données contenant du bruit ou des valeurs erronées. Le modèle ne sera donc pas capable de dégager de patterns à partir du jeu de données.
Une autre cause peut être un modèle hautement biaisé à cause de son incapacité à capturer la relation entre les exemples d’entraînement et les valeurs cibles. La troisième raison peut être un modèle trop simple, tel qu’un modèle linéaire entraîné sur des scénarios complexes.
En voulant éviter l’overfitting, il existe un risque de provoquer l’underfitting. Ceci peut survenir en interrompant le processus d’entraînement plus tôt, ou en réduisant sa complexité par l’élimination des entrées les moins pertinentes.
Si l’entraînement est interrompu trop tôt ou que des caractéristiques importantes sont supprimées, l’underfitting peut survenir. Dans les deux cas, le modèle sera incapable d’identifier les tendances au sein du dataset.
Il est donc essentiel de trouver l’ajustement idéal pour que le modèle identifie les patterns dans les données d’entraînement, sans pour autant mémoriser les détails trop précis. C’est ce qui permettra au modèle de généraliser et de prédire les autres échantillons de données avec précision.
Comment éviter l’overfitting ?
Pour éviter l’overfitting, il faut donc réévaluer le modèle à chaque fois sur des données non vues pendant l’entraînement.
Une bonne pratique est de séparer son jeu de données initiales en un jeu d’entraînement (train set) et un jeu de test (test set). Le premier servira à entraîner le modèle. Le jeu de test constitué de données non vues (unseen data) servira donc à tester la manière dont se généralise le modèle.
On ne pourra conclure sur les performances du modèle qu’avec les performances du jeu de test, et non pas avec les performances sur le jeu d’entraînement qui risque d’être appris par cœur.
Comment choisir les données d’entraînement et de test ?
La manière la plus simple et la plus utilisée consiste à séparer les données aléatoirement. Le module sklearn.model_selection de Python propose à cet effet la fonction train_test_split. En lui fournissant un jeu de données, cette fonction crée une partition de celui-ci ce qui permet d’obtenir le jeu de test et le jeu d’entraînement.

Cependant, cette séparation se fait de manière aléatoire. Il existe donc un risque de créer par hasard des jeux de données non représentatifs.
Pour éviter de valider un modèle sur des données non représentatives, une méthode est de reproduire la procédure d’entraînement sur un jeu puis de tester sur un autre jeu plusieurs fois, puis de moyenner les résultats. Cela permet de moyenner les effets aléatoires et d’obtenir une estimation de la performance sur des données non vues aléatoirement choisies.
Cette validation de modèle s’appelle la validation croisée ou cross validation en anglais.
Une validation croisée est composée de plusieurs folds. Chaque fold est une partition du jeu de données en deux ensembles (jeu d’entraînement et jeu de test). La validation croisée consiste pour chaque fold à entraîner le modèle sur le jeu d’entraînement puis de l’évaluer sur le jeu de test.
Nous pouvons ensuite estimer la performance du modèle en évaluant la performance des prédicteurs de chaque fold sur le jeu de test de chacun des folds, puis en moyennant leurs performances.
Cette approche permet également d’accéder à l’écart-type de ces performances, ce qui permet de se faire une bonne idée de la variabilité du modèle en fonction du jeu d’entraînement. Si la variabilité est élevée, alors il faudra faire d’autant plus attention au choix de notre jeu d’entraînement. Au contraire, avec une faible variabilité, le choix du jeu d’entraînement n’a pas beaucoup d’importance.

Quelles sont les sources d’erreur d’un modèle ?
Pour un modèle de régression, le premier critère d’évaluation est l’erreur quadratique moyenne ou MSE pour mean squared error en anglais.
Notre jeu de données D est constitué de n réalisations (xi, yi) d’un vecteur aléatoire de même loi qu’un couple de variables aléatoires (X,Y) qui sont reliés par la relation Y = f(X) + eps avec eps une variable aléatoire d’espérance nulle et de variance sigma², c’est-à-dire le bruit des données.
On peut décomposer l’erreur quadratique moyenne sur D d’un estimateur comme la somme :
- Du carré du biais de l’estimateur (qui quantifie à quel point les étiquettes prédites sont loin de la réalité)
- De la variance de l’estimateur (qui quantifie comment varie les étiquettes pour un même individu selon les données d’entrée)
- De la variance du bruit aussi appelée erreur irréductible
Ainsi, un estimateur biaisé avec une faible variance peut obtenir de meilleures performances qu’un estimateur non biaisé avec une grande variance.
Dans de très nombreux cas, l’overfitting apparaît dans les cas où l’on choisit un estimateur peu biaisé avec une forte variance. Des modèles complexes peuvent posséder ces caractéristiques comme les régressions polynomiales de trop grand ordre (cf schéma 1). Le choix de modèles plus simples et a priori “moins bons” car biaisés, peut donc permettre d’obtenir de meilleures performances si leur variance est faible !
Si vous voulez en apprendre plus sur l’overfitting et l’intelligence artificielle appliquée aux images :