Dans un article précedent, nous avons défini le NLP- Natural Language Processing. Dans cet article, nous allons nous intéresser à l’une de ses méthodes principales, le word embedding. Le word embedding (plongement de mots) désigne un ensemble de méthode d’apprentissage visant à représenter les mots d’un texte par des vecteurs de nombres réels. Dans cet article, vous allez explorer trois grandes méthodes pour représenter un mot sous forme d’un vecteur :
- Méthode 1 : One Hot Encoding
- Méthode 2 : Image Embedding
- Méthode 3 : Word Embedding
One hot encoding : Une méthode qui transforme les lettres en valeurs numériques
Pour illustrer l’encodage, prenons la phrase suivante :
"I think therefore I am" Le principe est d’attribuer un indice à chaque mot du vocabulaire. Le vocabulaire se présente alors sous forme d’un dictionnaire :
{'am': 0, 'i': 1, 'therefore': 2, 'think': 3} Ici, le vocabulaire est composé les 4 mots uniques de notre corpus. La méthode consiste alors à représenter le mot du vocabulaire sous forme de vecteur de dimension 4 (taille du vocabulaire) qui a toutes ses valeurs nulles à l’exception de l’index du mot.
Onehot('i')=0 1 0 0 Avec cette représentation, tous les mots ont la même distance et la même similitude. L’encodage one hot n’apporte donc qu’une information selon laquelle un mot est différent d’un autre.
Comment transformer des images en valeurs numériques à l'aide de l'image Embedding ?
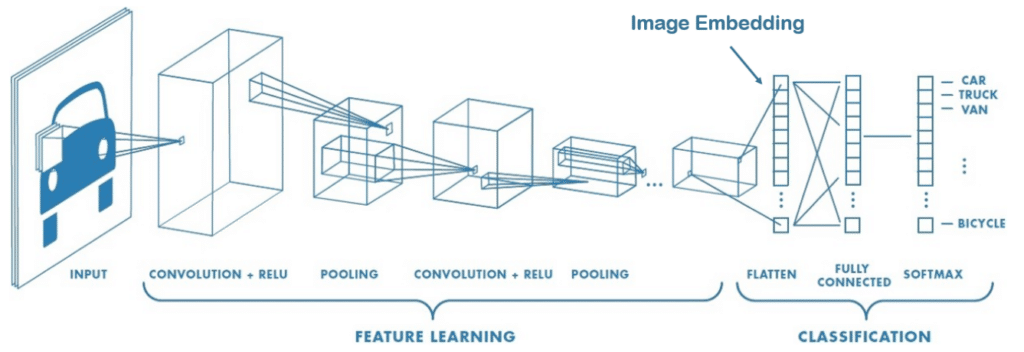
La dimension d’une image est définie par son nombre de pixel. Dans un article précédent sur les Convolutionnal neural network, nous utilisons des convolutions pour l’extraction de caractéristiques plus pertinentes que la valeur des pixels. Par exemple, les noyaux servant à détecter les bords pourraient être utiles pour classifier certaines formes géométriques.
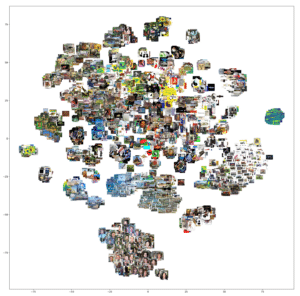
L’image embedding est capable en utilisant les convolutions/pooling d’encoder l’image et d’extraire des relations de linéarité entre des propriétés (style artistique, forme spécifique…) et les nouvelles caractéristiques de notre image.
Définition du Word Embedding
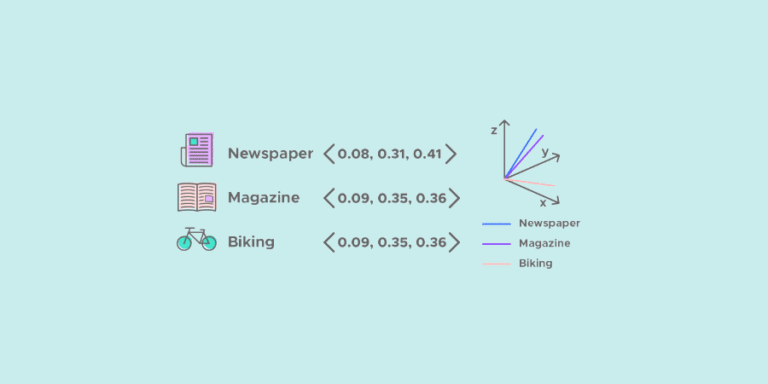
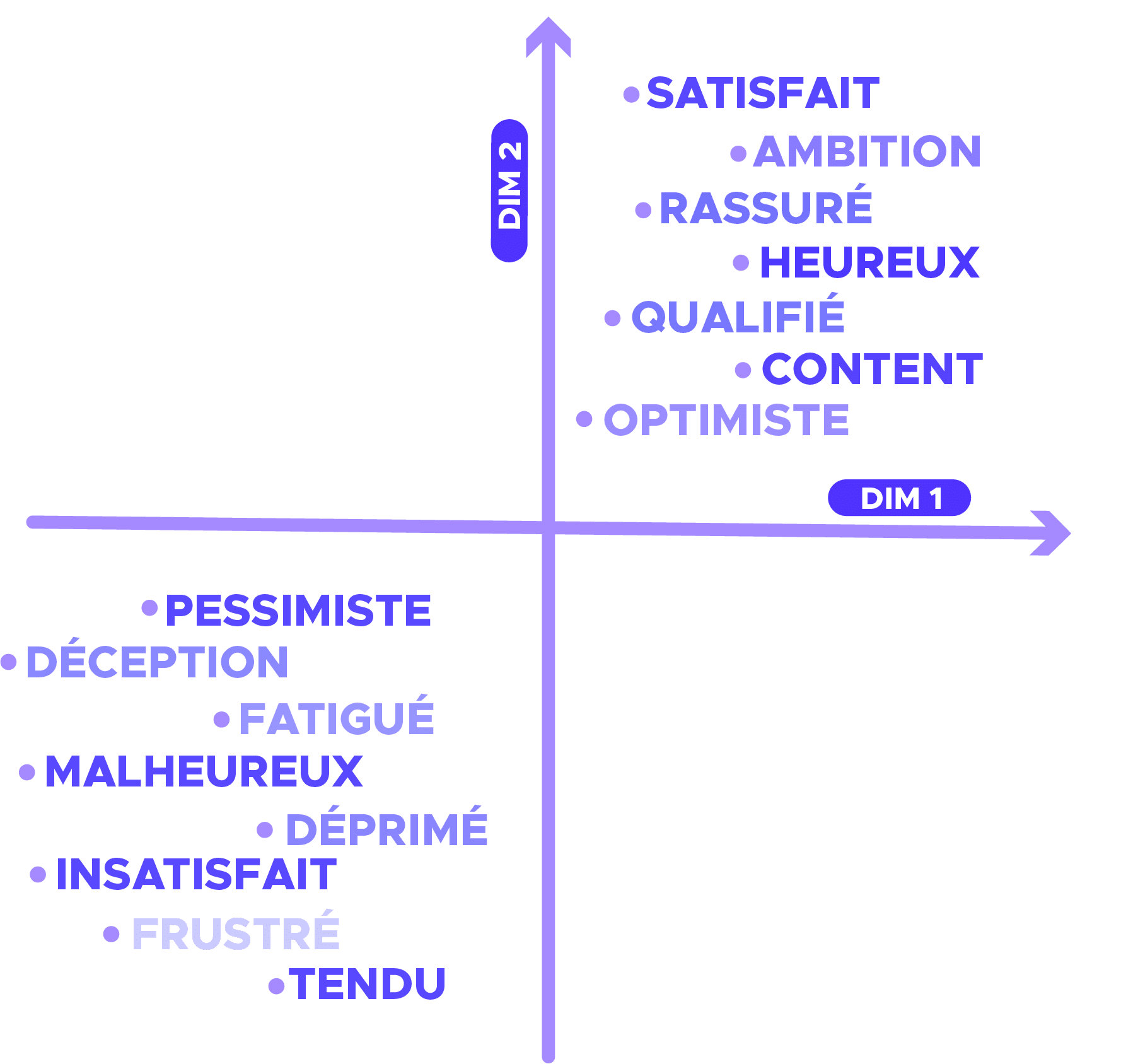
Par analogie, le word embedding est capable en réduisant la dimension de capturer le contexte, la similarité sémantique et syntaxique (genre, synonymes, …) d’un mot. Par exemple, on pourrait s’attendre à ce que les mots « chien » et « chat » soient représentés par des vecteurs relativement peu distants dans l’espace vectoriel où sont définis ces vecteurs.
Comme pour les images, nous souhaitons que ça soit le modèle qui choisisse les caractéristiques les plus pertinentes représentant le mot. Par exemple, la caractéristique « être vivant » pourrait être intéressante pour différencier « chien » et « ordinateur », et rapprocher « chien » et « chat ».
Matrice d’embedding
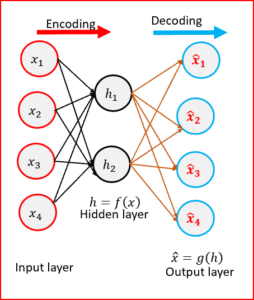
La méthode d’embedding qui généralement utilisé pour réduire la dimension d’un vecteur est d’utiliser le résultat que retourne une dense layer comme embedding, c’est à dire de multiplier une matrice d’embedding W par la représentation « one hot » du mot :
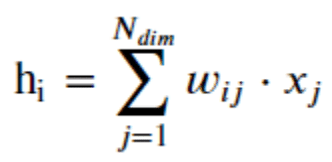
Sous forme vectorielle :
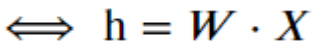
Maintenant que l’on a défini la méthode de réduction de dimension (de compression de l’information), comment est-ce qu’on entraîne la matrice d’embedding W ?
Entraînement de la matrice d’embedding – Problème de classification
Une première façon de trouver la matrice d’embedding est de l’entraîner sur un problème supervisé. De ce fait, nous allons utiliser cette représentation des mots pour résoudre un problème de sentiment analysis sur les reviews IMBD. Le jeu de données comporte 25000 critiques de films (plus d’informations sur le jeu de données choisi).
Il est alors possible d’entraîner la matrice W du word embedding en même temps que l’entraînement du problème de classification.
Mise en forme des données :
Pour mettre en forme les données, il est nécessaire de vectoriser le corpus de texte, en transformant chaque review en une séquence d’entiers (chaque entier étant l’index d’un mot) :
tokenizer.texts_to_sequences([‘hello my dear readers’]) -> [[4422, 10, 2974, 6117]]
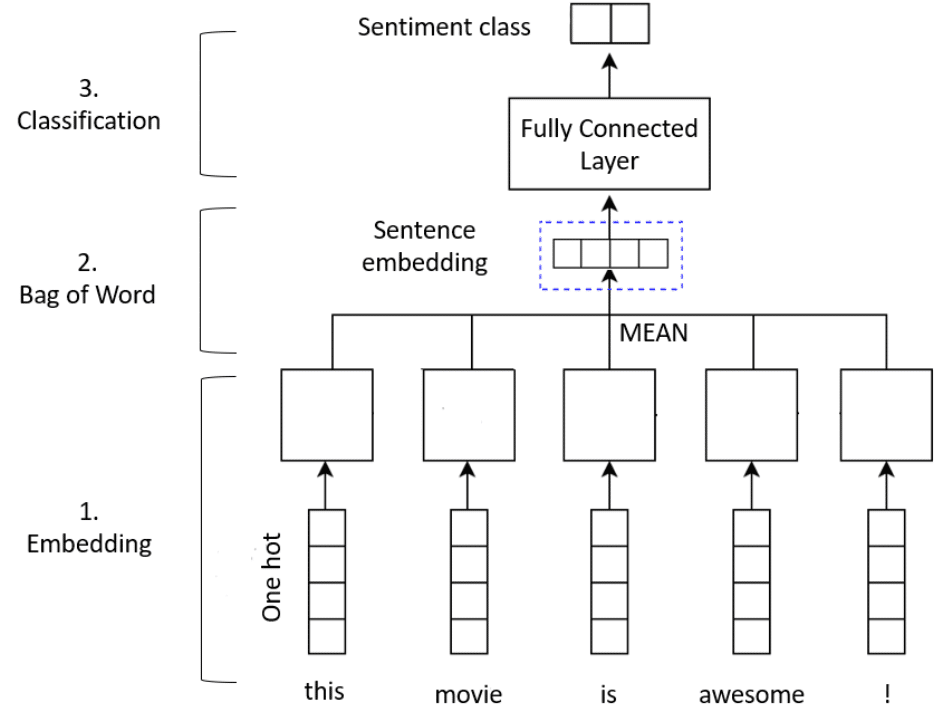
Notre modèle sera un simple bag of word avec une méthode d’embedding :
- La couche Embedding va transformer chaque index de mots en vecteur d’embedding. La matrice W de l’embedding sera apprise au fur et à mesure que le modèle s’entraîne. Les dimensions résultantes sont : (lot, séquence, embedding).
- Ensuite, la couche GlobalAveragePooling1D renvoie un vecteur de sortie de longueur fixe pour chaque exemple en faisant la moyenne sur la dimension de séquence. Cette transformation consiste à faire un bag of word et permet au modèle de gérer des entrées de longueur variable.
- Enfin, comme nous sommes face à un problème de classification (review positive ou négative), il est nécessaire d’ajouter des couches Dense pour classifier le sentiment de la review.
Mise en pratique
De cette façon, nous avons atteint sur le jeu de données de test une précision de 0.88. Ce score est difficilement atteignable à l’aide de méthodes classiques. Par ailleurs, nous aurions aussi pu utiliser une méthode tf-idf (à la place du bag of word) pour transformer notre séquence en vecteur.
Pour résumer :
Un modèle de ce type donne en général de meilleur résultat que les approches traditionnelles. Il permet également de réduire la dimension du problème et par conséquent la tâche d’apprentissage. Néanmoins, comme nous ne donnons qu’une information sur le sentiment, le word embedding ne capture que difficilement d’autre relation que ça.
Dans un prochain article, nous allons entraîner la matrice d’embedding de manière non-supervisé à l’aide du célèbre algorithme word2vec. Comme l’entraînement se fait de manière non supervisée, nous allons éviter le biais lié à la résolution d’un problème supervisée.
Cet article vous a plu ? Vous souhaitez aller plus loin dans votre apprentissage de la data science ?