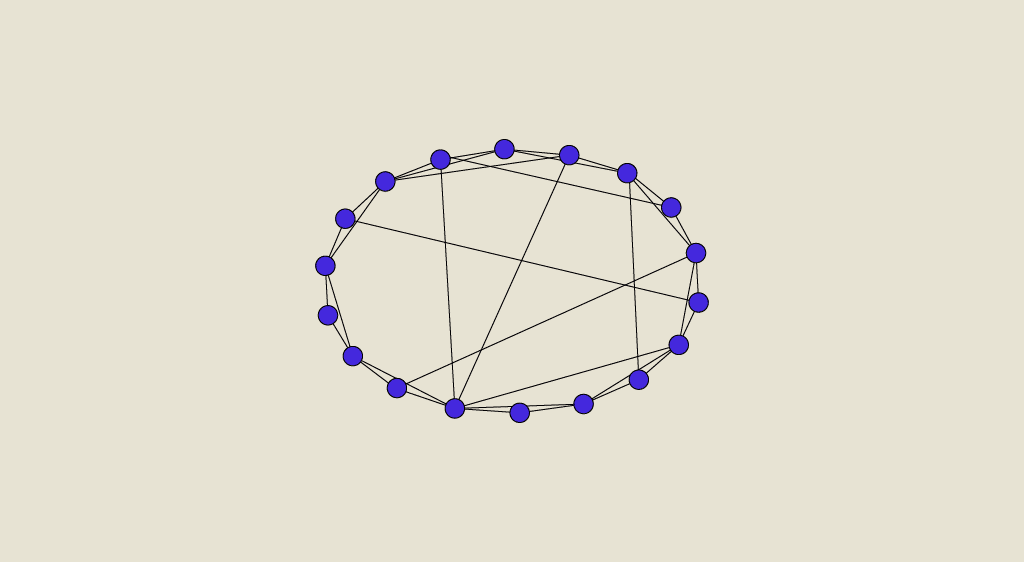
NetworkX est une librairie python très utile pour modéliser vos données sous forme de graphes. Elle contient également des algorithmes classiques de théorie des graphes (Dijkstra, PageRank, SImRank...) que nous allons présenter dans cet article.
Qu’est ce qu’un graphe ? Introduction à la Théorie des Graphes
Un graphe est un ensemble de nœuds (représentant individu, villes, produits, texte, image, etc.), et d’arêtes reliant un sous-ensemble de ces nœuds. Le degré d’un nœud du graphe est son nombre de voisins (les sommets reliés à lui par des arêtes).
Les arêtes peuvent être unilatérales ou symétriques, un graphe peut donc être orienté ou non.
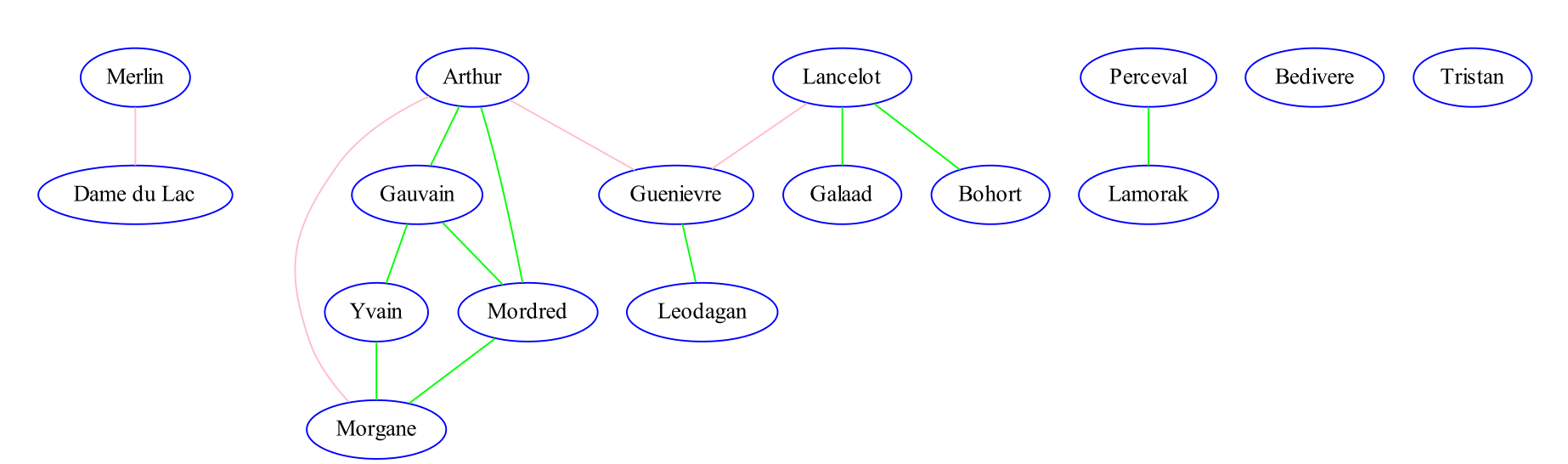
Le graphe non orienté représente les relations de parentés (en vert) et d’amour (en rose ) des personnages principaux de la table ronde :
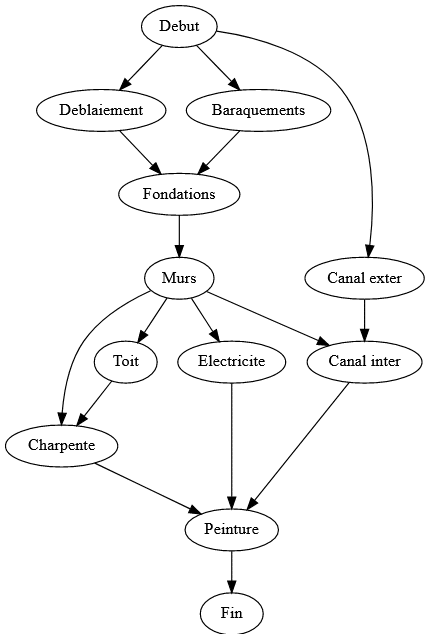
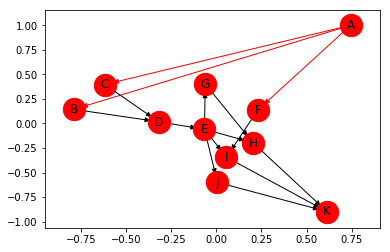
On peut choisir de pondérer les arêtes d’un graphe avec des poids modélisant le coût ou la proportion d’usage de ce chemin. Par exemple, sur le graphe précédent, le coût des arêtes serait le nombre de jours nécessaires pour réaliser la tâche.
Applications :
La théorie des graphes recouvre un ensemble vaste d’applications : modélisation de réseaux (infrastructures, sociaux…), de gestion de stocks, d’emploi du temps et leurs problématiques associées :
- Comment établir l’itinéraire le plus court/optimal ? problème du voyageur de commerce.
- Comment placer des infrastructures (électriques, fibre…) de façon optimale ? problème de couverture minimale.
- Comment allouer des locations à des clients ou des cours à des apprenants sans chevauchement ? problème de coloration.
Fonctions de base et principales utilisations de NetworkX
Construire notre premier graphe :
Le code suivant va construire un graphe, on commence par lui ajouter ses arêtes (g.addnode) et ses nœuds (g.add edge) (on peut en ajouter plusieurs à la fois avec les fonctions: g.add nodes from et g.add edges from), on affiche ensuite le graphe créé :
On peut aussi synthétiser rapidement des propriétés du graphe via les méthodes de NetworkX:
- nombre de noeuds avec number_of_nodes, nombre d’arêtes avec number_of_edges
- diamètre = distance maximale entre deux noeuds : diameter
Les Sept Ponts de Koenigsberg, quel est ce problème historique ?
Un des premiers problèmes de la théorie des graphes est celui des ponts de Koenigsberg. Il fut présenté en 1736 au mathématicien Euler sous la forme suivante :
« Peut-on parcourir les 7 ponts de la ville en empruntant chaque pont une seule fois ? »: Euler remarqua que l’ordre du parcours n’avait aucune influence et modélisa le problème sous forme d’un graphe : les différents quartiers étant ses nœuds, reliés entre eux par les ponts, qui sont donc les arêtes du graphe.
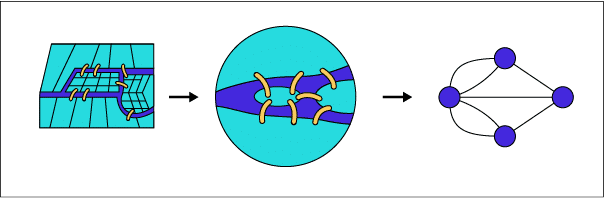
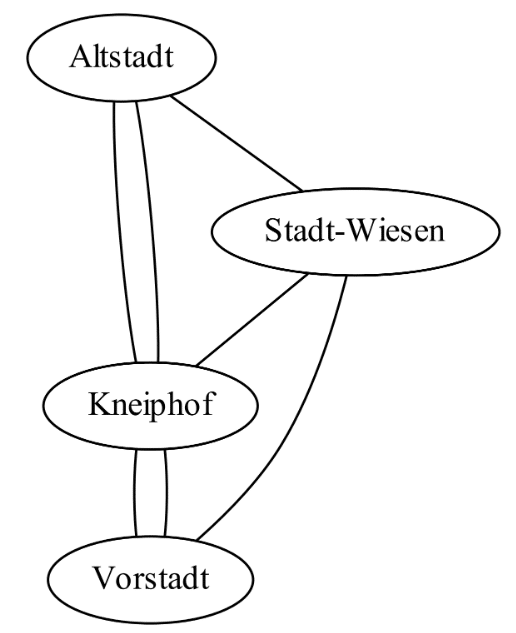
Alors quelle est la solution selon vous ?
Si l’on arrive via un pont dans un quartier, il faut aussi le quitter par un (autre) pont. Le nombre d’arrivées dans un quartier est donc égale au nombre de départs depuis ce quartier. Il en résulte que chaque quartier doit être relié aux autres via un nombre pairs de ponts.
La solution du problème dépend donc du degré (nombre de voisins/ponts attenants) des nœuds : si ceux-ci sont tous pairs alors un chemin empruntant tous les ponts une seule fois, nommé chemin eulérien, existe.
Comment trouver le chemin le plus court avec le Problème du Voyageur de Commerce ?
Un autre problème classique de théorie des graphes est celui du voyageur de commerce : les nœuds du graphe sont un ensemble de villes ou de clients à livrer tandis que les arêtes sont les infrastructures routières, munies d’un poids modélisant la distance associée. On cherche à desservir toutes les villes en empruntant le chemin le plus court.
Dans le cas où les poids du graphe sont positifs (ou du moins s’il n’y a pas de cycle avec un poids négatif) une solution à ce problème est donnée par l’algorithme de Dijkstra, disponible via la fonction nx.shortest_path().
Un dresseur plus malin que les autre cherche à finir l’aventure en empruntant le moins de chemin possible, le script suivant lui permettra de rallier la ligue en un temps record :
Couverture Minimale d’un réseau
Le problème de l’arbre couvrant minimal se pose lorsqu’une entreprise cherche à construire un réseau (pétrole, fibre) reliant un ensemble de foyers de façon optimale.
Dans le graphe associé à ce problème, les nœuds sont les clients à relier, les arêtes l’ensemble des emplacements d’infrastructures possibles et les poids sont leurs coûts de construction.
On cherche à déterminer le sous ensemble d’arêtes reliant l’ensemble des nœuds qui minimise le coût total, nommé arbre couvrant minimal.
NetworkXdispose d’une fonction résolvant ce problème : l’algorithme de Kruskal implémenté dans la méthode nx.tree.minimum_spanning_tree
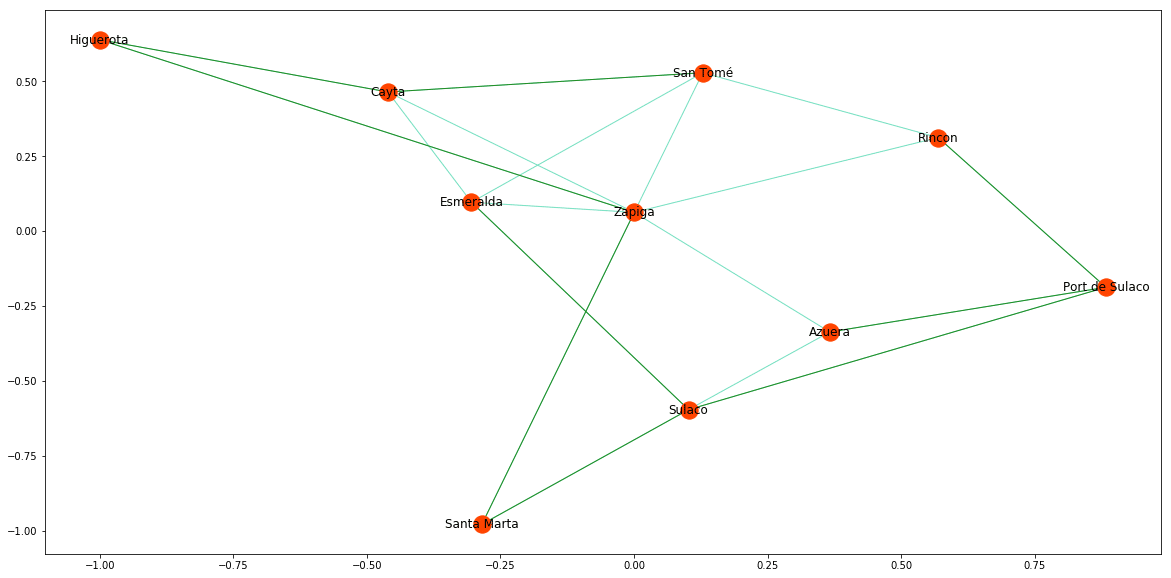
Un industriel cherche à construire un réseau de chemins de fer dans le province fictive du Costaguana, il veut relier toute les villes mais dispose d’un budget limité, il modélise la situation via le graphe suivant :
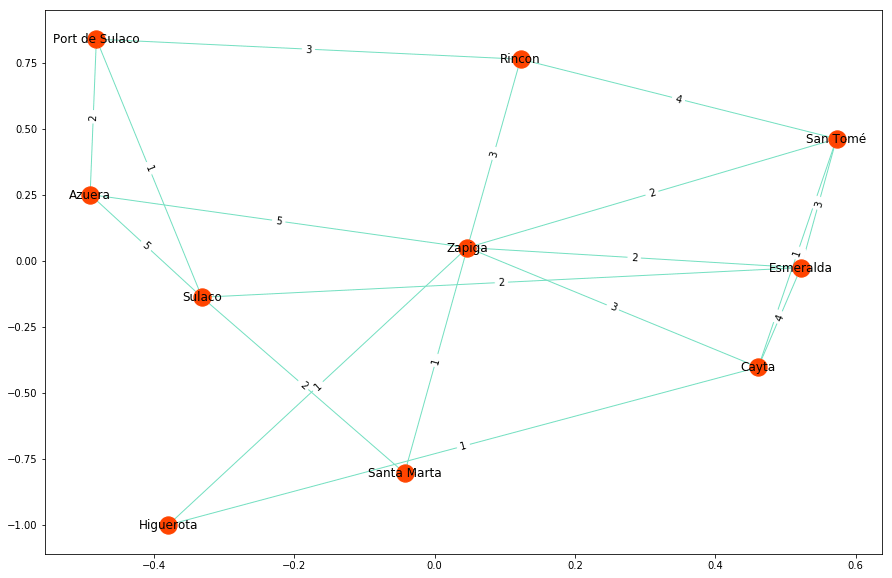
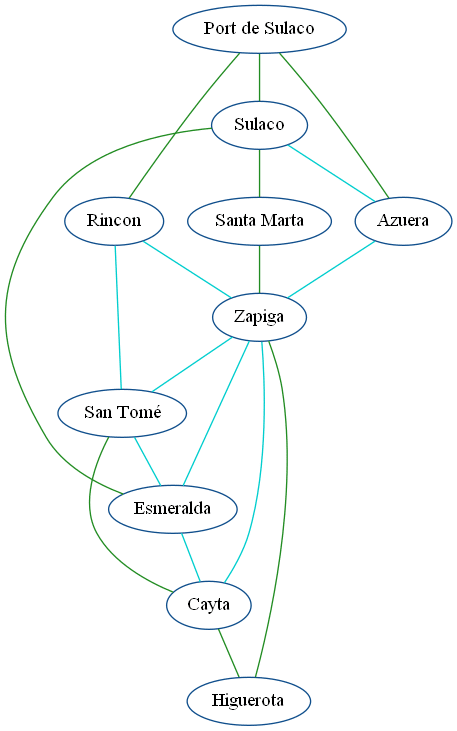
Page Rank :
Le page rank est un algorithme utilisé par Google pour calculer la popularité des pages web : celles avec le plus gros score sont affichées en premier.
Pour mesurer ce score, on représente le web par un graphe dont les nœuds sont les sites web et les arêtes sont les liens hypertextes/entre les pages. Le principe est le suivant : les scores initiaux des graphes sont uniformes, on va ensuite parcourir le graphe au hasard en sautant d’un site à un autre de façon aléatoire (on ne prend donc pas en compte les sites visités précédemment), et à chaque passage par un site web on va actualiser son score.
À la fin de l’algorithme, les scores des sites seront proportionnels aux probabilités de passage : les sites les plus visités par le surfeur/marcheur aléatoire auront un score important.
L’un des principaux problèmes du PageRank est son coût de calcul très élevé. Un algorithme connexe, le SimRank, qui calcule la calcule la similarité entre les pages webs est également implémenté par NetworkX
Conclusion
NetworkX recouvre donc un ensemble de méthodes efficaces répondant à un vaste champ d’applications. Découvrez davantage de ses applications à la Data Science avec notre module Machine Learning et Théorie des graphes avec NetworkX de notre cursus Data Scientist.