La courbe ROC (Receiver Operating Characteristic) et sa métrique associée AUC (Area Under the Curve) sont des outils fondamentaux pour l’évaluation des modèles de classification en apprentissage automatique. Ces métriques fournissent des informations cruciales sur la capacité d’un modèle à distinguer les classes, particulièrement dans les scénarios de classification binaire.
Les fondamentaux de la ROC AUC
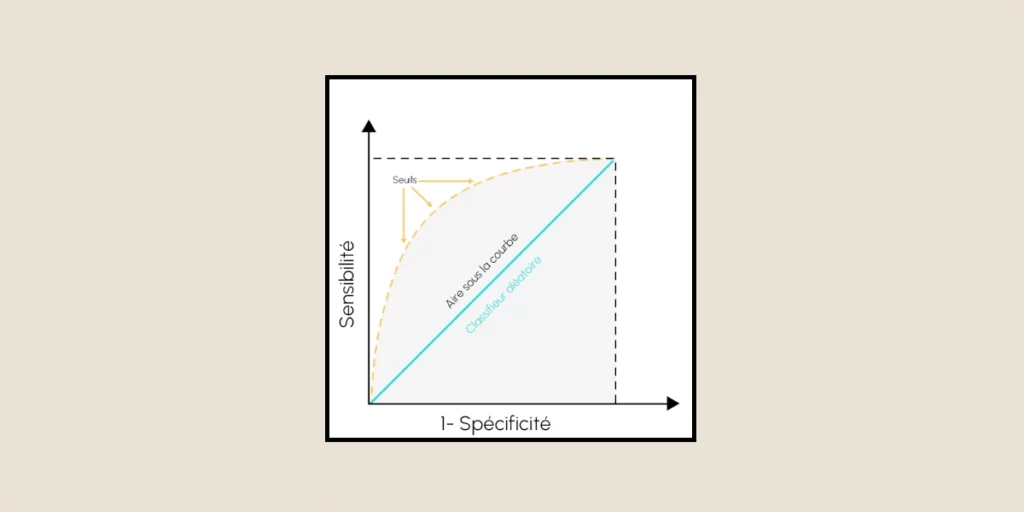
La courbe ROC est, dans son essence, une représentation graphique qui illustre la performance d’un modèle de classification à travers différents seuils de décision. Cette courbe trace la relation entre deux métriques de performance critiques : la sensibilité (aussi connue comme le taux de vrais positifs) et la spécificité complémentaire au taux de faux positifs). Lorsque le seuil de décision du modèle change, ces taux évoluent, créant une courbe qui révèle la capacité discriminative du modèle.
L’aire sous cette courbe, connue sous le nom d’AUC, fournit une valeur scalaire unique qui quantifie la performance globale du classificateur. Un classificateur parfait atteint une AUC de 1.0, tandis qu’une prédiction aléatoire donne une AUC de 0.5, représentée par une ligne diagonale sur le graphique ROC.
Comprendre la performance du modèle à travers la ROC AUC
Lors de l’évaluation d’un modèle de classification, la courbe ROC fournit des informations précieuses sur ses caractéristiques de performance. La courbe commence dans le coin inférieur gauche (0,0) et s’étend jusqu’au coin supérieur droit (1,1). Le chemin qu’elle emprunte entre ces points nous renseigne sur la capacité du modèle à identifier correctement les cas positifs et négatifs.

Un avantage majeur de la ROC AUC est son insensibilité au déséquilibre des classes. Cela la rend particulièrement précieuse pour les applications réelles où une classe peut être significativement plus présente que l’autre. Par exemple, dans le diagnostic médical, où le nombre de patients sains dépasse généralement largement celui des patients malades, la ROC AUC fournit une évaluation équilibrée de la performance du modèle.
Applications pratiques et interprétation
Dans les applications d’apprentissage automatique, la ROC AUC remplit plusieurs fonctions importantes. Elle aide à la sélection de modèles, au réglage des paramètres et à la comparaison de différents algorithmes de classification. Cette métrique est particulièrement utile lorsque le seuil de décision optimal n’est pas connu à l’avance ou pourrait nécessiter des ajustements selon des exigences spécifiques.
Prenons l’exemple d’un test diagnostique médical : une AUC élevée indique que le test peut efficacement distinguer entre les états sain et malade. La courbe ROC permet aux professionnels de santé de choisir un seuil optimisant la sensibilité (identification correcte des patients malades) et la spécificité (identification correcte des patients sains) en fonction des coûts relatifs des faux positifs et des faux négatifs.
Concepts avancés et considérations
Bien que la ROC AUC soit principalement associée à la classification binaire, elle peut être étendue aux problèmes multi-classes à travers diverses approches. Une méthode courante est l’approche « un-contre-tous », où des courbes ROC séparées sont générées pour chaque classe contre toutes les autres.
La matrice de confusion joue un rôle crucial dans la compréhension de la ROC AUC. Elle fournit les décomptes fondamentaux des vrais positifs, vrais négatifs, faux positifs et faux négatifs qui forment la base du calcul des taux tracés dans la courbe ROC.
Implémentation et outils

Les frameworks modernes d’apprentissage automatique fournissent des outils robustes pour calculer et visualiser la ROC AUC. Des bibliothèques comme scikit-learn offrent des implémentations directes via des fonctions comme roc_auc_score, facilitant l’intégration de cette métrique dans les pipelines d’évaluation de modèles.
Meilleures pratiques et limitations
Bien que la ROC AUC soit une métrique puissante, il est important de comprendre ses limitations. Elle ne prend pas en compte les différences de coût entre faux positifs et faux négatifs, ce qui limite son applicabilité dans certains contextes. De plus, dans les jeux de données très déséquilibrés, des métriques complémentaires comme les courbes précision-rappel peuvent offrir une meilleure évaluation de la performance.
Guide d'implémentation pratique
La compréhension technique de l’implémentation des calculs de la ROC AUC est cruciale pour les praticiens en apprentissage automatique. Le processus commence par les probabilités prédites par le modèle pour chaque classe. Ces probabilités sont ensuite triées pour créer différentes valeurs de seuil, et pour chaque seuil, le taux de vrais positifs et le taux de faux positifs sont calculés.
Techniques d'optimisation de la performance
Pour maximiser l’efficacité de la ROC AUC dans l’évaluation des modèles, plusieurs techniques d’optimisation peuvent être employées. L‘ingénierie des caractéristiques joue un rôle crucial dans l’amélioration de la performance du modèle. De plus, le traitement approprié des valeurs manquantes et des valeurs aberrantes peut significativement impacter la forme de la courbe ROC et l’AUC résultante.

Applications sectorielles spécifiques
Différents secteurs ont des exigences et des considérations uniques lors de l’application de l’analyse ROC AUC. Dans les services financiers, les courbes ROC aident à évaluer les modèles de scoring de crédit. Le secteur de la santé utilise intensivement la ROC AUC dans les tests diagnostiques. Dans les applications de cybersécurité, la ROC AUC aide à évaluer les systèmes de détection d’anomalies.
Conclusion
La ROC AUC reste l’une des métriques les plus importantes pour l’évaluation des modèles d’apprentissage automatique. Sa capacité à fournir une évaluation indépendante du seuil de la performance du classificateur, combinée à son insensibilité au déséquilibre des classes, en fait un outil inestimable dans l’arsenal du praticien en apprentissage automatique. La comprendre et l’interpréter correctement est essentiel pour développer des modèles de classification efficaces et prendre des décisions éclairées concernant leur déploiement dans des applications réelles.