Des statistiques à l'étude des mouvements des corps en passant par le cours des actions financières en bourse, les fonctions sont utilisées dans tous les domaines. A chaque fois qu’on appuie sur une touche d’un clavier d’ordinateur ou qu’on manipule un téléphone portable, on peut se dire qu’en tâche de fond plusieurs fonctions se relaient pour appliquer des transformations et fournir un résultat.
Le présent article se propose de présenter quelques points essentiels pour comprendre qu’est ce que qu’une fonction.
1. Définition d’une fonction et quelques exemples
Une fonction , en mathématique, permet de définir un résultat associé à une valeur appartenant à un domaine d’entrée. Le résultat peut être obtenu à la suite de différentes opérations arithmétiques, de différents procédés (comme les résolutions d’équations ou les passages à la limite).
Comme exemple de définition formelle, on peut donner l’exemple de définition mathématique suivante :
Une fonction f est une manière d’associer à tout nombre réel x un seul nombre réel y.
Dans l’exemple de définition ci-dessus:
- x correspond à la variable de la fonction (pour le cas des fonction à une seule variable)
- y correspond à l’image de la variable x par la f (on notera ‘image d’une fonction f(x) ou y = f(x))
La manière d’associer un nombre à un autre peut se faire:
- Au moyen d’une formule mathématique (exemple: f(x) = 4x + 10).
- Au moyen d’une courbe(exemple de la courbe donnant l’évolution de la température en fonction du temps).
- Au moyen d’un instrument de mesure (exemple du compteur d’électricité).
- Au moyen d’un tableau de valeurs donnant la correspondance entre 2 lignes de valeurs.
Le calcul effectif du résultat peut être effectué au moyen de fonctions informatiques qui effectueront des opérations sur des données d’entrée. La fonction informatique va alors consister en la description de la méthode pour obtenir un résultat à partir de paramètres donnés en entrée (on va parler d’algorithme).
En théorie des ensembles, une fonction peut être définie comme la relation entre deux ensembles qui, à chaque élément d’un ensemble de départ, va faire correspondre un ou plusieurs éléments de l’ensemble d’arrivée.
2. Principe général et exemples de fonctions
Si l’on considère 2 groupes de nombres (un groupe de départ et d’arrivé ci-dessous) :

La correspondance entre les deux groupes est assurée par la fonction f (correspondance qui en passant pourrait avoir un nom différent de f). Sur la base de cette représentation, on peut aisément voir qu’on pourrait substituer à f, la notation tabulaire ci-dessous :
Comme interprétation, tous les nombres de l’ensemble d’arrivée sont appelés les images des nombres de l’ensemble de départ. Tous les nombres de l’ensemble de départ sont les antécédents des nombres de l’ensemble d’arrivée.
Pour définir de manière rigoureuse une fonction en mathématique, il est nécessaire en pratique de définir les différentes propriétés de cette dernière portant sur sa régularité, ses variations, son intégrabilité, etc.
A cet effet, il existe différents types de fonctions parmis lesquelles on peut citer :
- Les fonctions constantes qui associent toujours le même résultat à un ensemble de valeurs (exemple f(x) = 5).
- Les fonction linéaires qui sont toujours de la forme f(x) = ax (a étant un nombre)
- Les fonctions affines (utilisées dans plusieurs algorithmes de machine learning) de la forme f(x) = ax + b (a et b étant des nombres).
3. Ensemble de définition d’une fonction
L’ensemble de définition d’une fonction f est l’ensemble de tous les nombres de l’ensemble de départ qui possèdent une image par l’application de f.
Par exemple, le domaine de définition de la fonction à une variable f(x) = 1/x est D = (-, 0)U(0, +) 0 étant exclu car la division par 0 étant impossible.
La définition d’une fonction pourra alors se faire sous la forme suivante :
f : D→R
X→f(x)
La définition montre clairement la correspondance entre les éléments de D ayant une image f(x) dans R (ici ensemble des nombres réels).
4. Représentation graphique d’une fonction
La représentation graphique d’une fonction correspond à la représentation visuelle de cette dernière dans un espace qu’on se fixe comme repère. En deux dimensions, on utilise le plus souvent un espace orthonormé (O, I, J) qui correspond à un espace dans lequel les points O, I et J forment un triangle rectangle isocèle en O (O étant l’origine du repère).
Les droites OI et OJ représentent respectivement les axes des abscisses et des ordonnées.
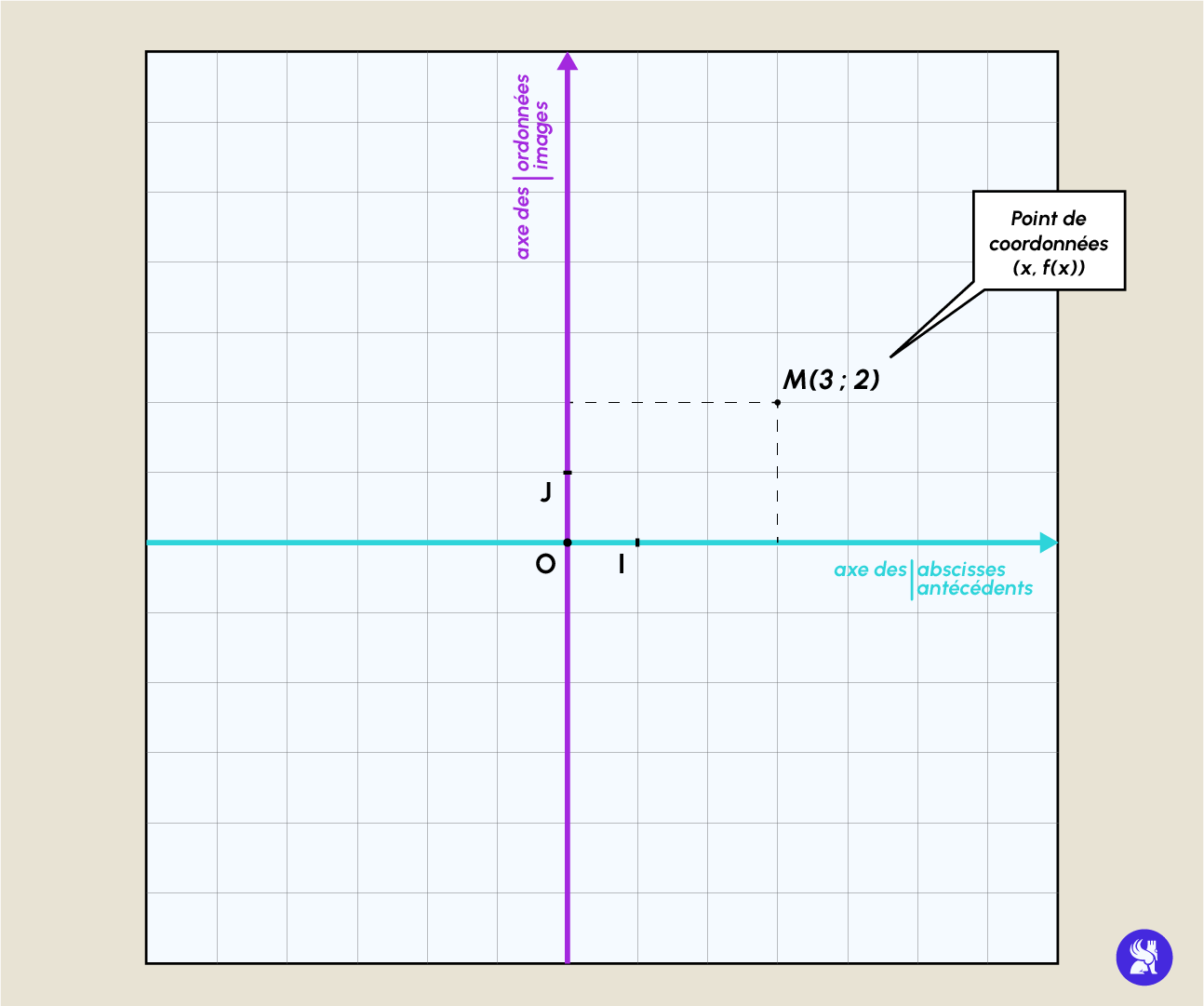
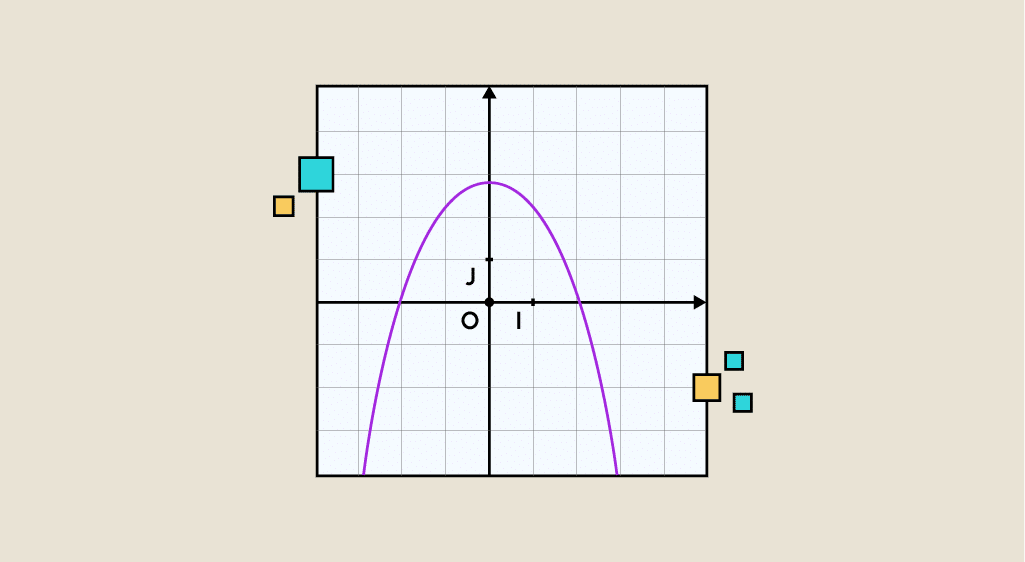
Soit f une fonction et soit D l’ensemble de définition associé. Dans un repère orthonormé (ou orthogonal) (O, I, J), l’ensemble des points M de coordonnées (x, f(x)) où x décrit un domaine D (on parle aussi souvent d’intervalle I) est appelé courbe représentative ou représentation graphique (noté Cf) de la fonction f. On dit alors que Cf (la courbe représentative de la fonction f) a pour équation y = f(x).
Par ailleurs, l’axe des abscisses (horizontal) représente les antécédents (donc les x) et l’axe vertical représente les images (les f(x)).
Dans l’exemple précédent ,si f(-1) = -4 cela signifie que Cf passe par le point de coordonnées (-1, -4). De cette manière, Cf va décrire l’ensemble de tous les points respectant l’équation y = f(x).
5. Sens de variation et extremums d’une fonction
La variabilité d’une fonction est une propriété qui est systématiquement étudiée.
Soit une fonction f définie sur un intervalle I. On a plusieurs possibilités en termes de variabilité de la fonction f sur I :
- f peut être croissante : on dit que f est croissante sur I si pour tout x et x’ dans I on vérifie: si x < x’ alors f(x) f(x’).
- f peut être strictement croissante : on dit que f est strictement croissante sur I si pour tout x et x’ dans I on vérifie: si x < x’ alors f(x) f(x’).

- f peut être décroissante : on dit que f est décroissante sur I si pour tout x et x’ dans I on vérifie: si x < x’ alors f(x) f(x’).
- f peut être strictement décroissante : on dit que f est strictement décroissante sur I si pour tout x et x’ dans I on vérifie: si x < x’ alors f(x) f(x’).
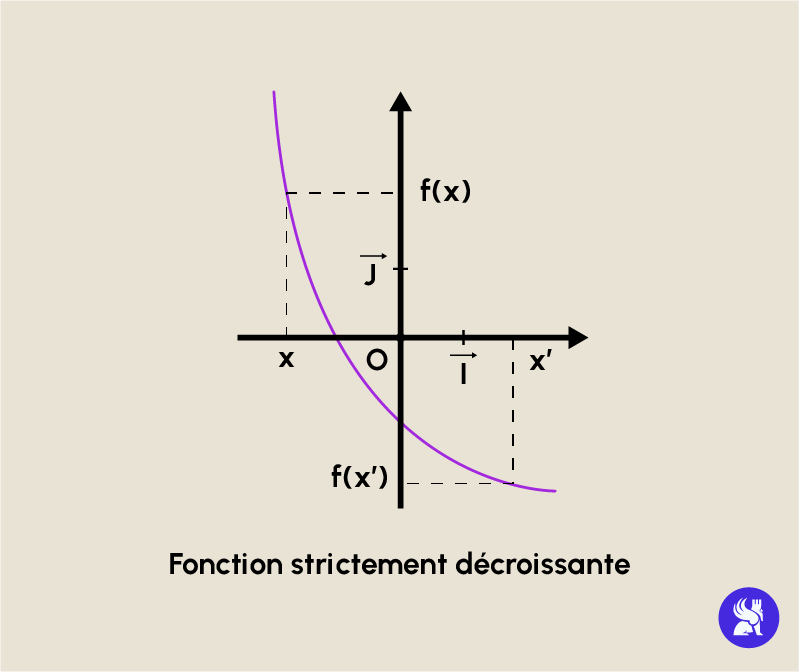
- f peut être constante : on dit que f est constante si il existe une constante d telle que pour tout x dans I on ait f(x) = d.
- f peut être monotone : on dit que f est monotone si f est croissante sur I ou (ou exclusif) décroissante sur I.
- f peut être strictement monotone : on dit que f est strictement monotone si f est strictement croissante ou strictement décroissante sur I.
Quand une fonction est croissante ou strictement croissante, les images f(x) sont rangées dans le même ordre que les antécédents. On dit alors que f conserve l’ordre.
En pratique, l’étude de la variabilité d’une fonction f se fait par le biais du tableau de variations (en deux lignes) qui aide ainsi à résumer les variations de cette dernière:
- La première ligne du tableau de variation donne les intervalles de l’ensemble de définition de la fonction. On y fait figurer les valeurs de l’ensemble de départ (les abscisses) sur lesquelles le sens de variation de la fonction change.
- Dans la deuxième ligne du tableau, on fait figurer des flèches représentant le sens de variation de la fonction.
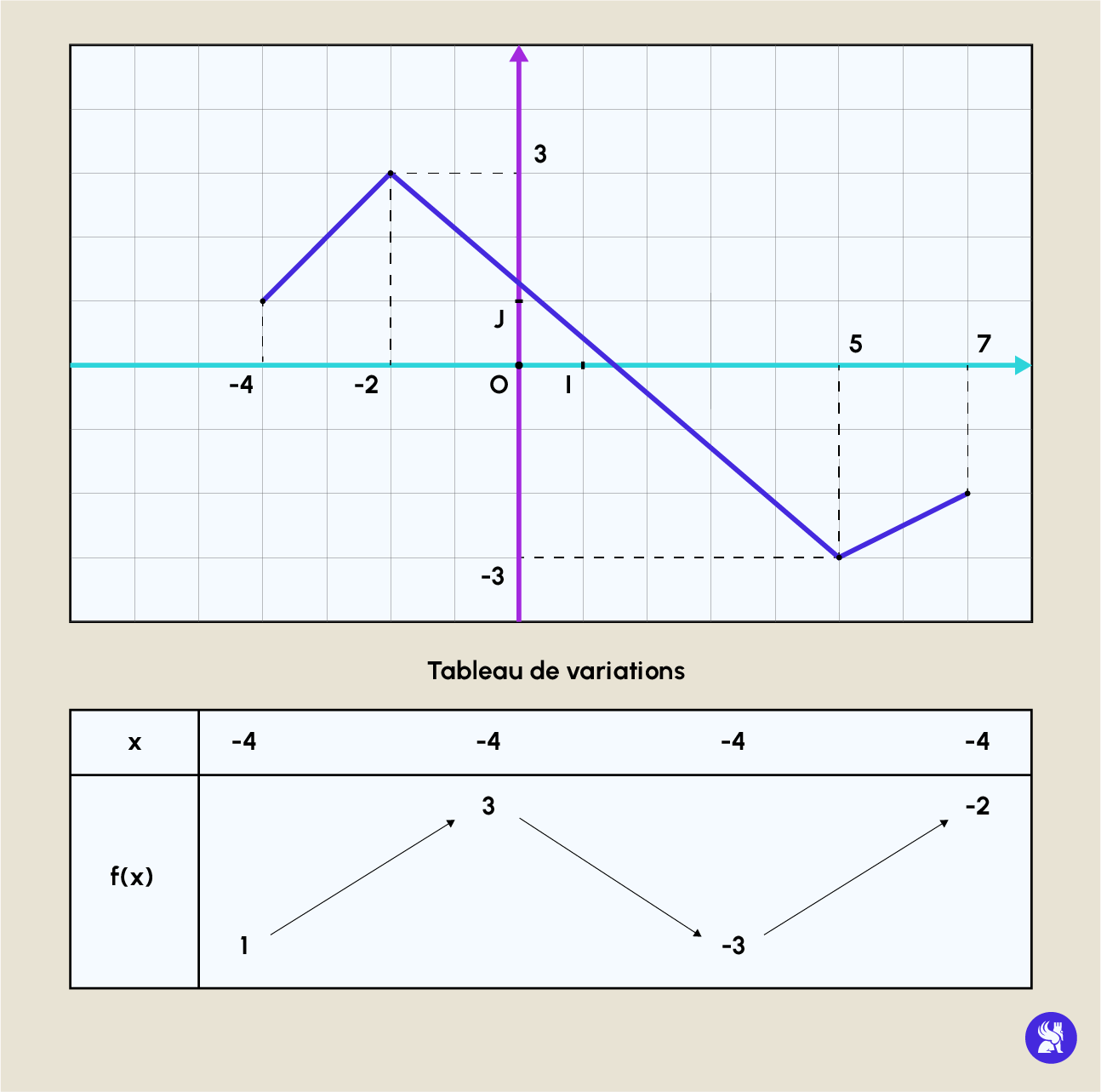
Les valeurs maximum M et minimum m d’une fonction f sur l’intervalle I correspondent respectivement à la valeur la plus grande et la plus petite de f(x) avec x variant dans I. Sur l’exemple ci-dessus, f atteint son maximum au point de coordonnées (-2, 3) (3 étant le maximum de la fonction) et son minimum au point (5, -3). Les valeurs maximum et minimum sont appelées les extremums de la fonction.
6. Les fonctions en data science
En analyse des données les fonctions sont utilisées à tous les niveaux. Par exemple en Python, les librairies utilisées pour appliquer des transformations sur les données sont des paquets de fonctions. Selon ce que l’on souhaite réaliser (par exemple manipuler du texte ou des images) on va utiliser un paquet de fonctions dédiées à la manipulation d’un type de données.
En Python, on a des fonctions pour à peu près tout faire (de la lecture à la sauvegarde en passant par la transformation des données ou des fichiers).
Si vous souhaitez en savoir plus sur l’utilisation des fonctions sur Python, découvrez nos parcours de formation.