Le clustering est une discipline particulière du Machine Learning ayant pour objectif de séparer vos données en groupes homogènes ayant des caractéristiques communes. C’est un domaine très apprécié en marketing, par exemple, où l’on cherche souvent à segmenter les bases clients pour détecter des comportements particuliers.
Dans de précédents articles, nous avions présenté deux algorithmes de clustering : celui des K-moyennes/ K-means et l’algorithme CAH-classification ascendante hiérarchique.
Il nous semblait essentiel de poursuivre cet apprentissage avec le DBSCAN.
L’algorithme DBSCAN
Le DBSCAN est un algorithme non supervisé très connu en matière de Clustering. Il a été proposé 1996 par Martin Ester, Hans-Peter Kriegel, Jörg Sander et Xiawei Xu.
Dans cet article, nous allons détailler son fonctionnement et comment l’implémenter en Python à l’aide de librairies tel que Scikit-Learn. Ses champs d’application sont divers : analyse cartographique, analyse de donnée, segmenter une image….
Le principe
Étant donnés des points et un entier k, l’algorithme vise à diviser les points en k groupes, appelés clusters, homogènes et compacts. Regardons l’exemple ci-dessous :
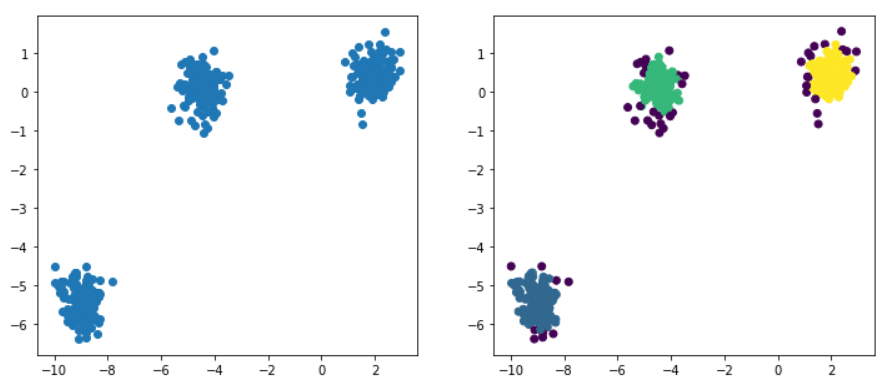
Le DBSCAN est un algorithme simple qui définit des clusters en utilisant l’estimation de la densité locale. On peut le diviser en 4 étapes :
- Pour chaque observation on regarde le nombre de points à au plus une distance ε de celle-ci. On appelle cette zone le ε-voisinage de l’observation.
- Si une observation compte au moins un certain nombre de voisins y compris elle-même, elle est considérée comme une observation cœur. On a alors décelé une observation à haute densité.
- Toutes les observations au voisinage d’une observation cœur appartiennent au même cluster. Il peut y avoir des observations cœur proche les unes des autres. Par conséquent de proche en proche on obtient une longue séquence d’observations cœur qui constitue un unique cluster.
- Toute observation qui n’est pas une observation cœur et qui ne comporte pas d’observation cœur dans son voisinage est considérée comme une anomalie.
Vous avez donc besoin de définir deux informations avant d’utiliser le DBSCAN :
Quelle distance ε pour déterminer pour chaque observation le ε-voisinage ? Quel est le nombre minimal de voisins nécessaire pour considérer qu’une observation est une observation cœur ?
Ces deux informations sont renseignées librement par l’utilisateur. Contrairement à l’algorithme des k-moyennes ou la classification ascendante hiérarchique, il n’y a pas besoin de définir en amont le nombre de clusters ce qui rend l’algorithme moins rigide.
Un autre avantage de DBSCAN est qu’il permet aussi de gérer les valeurs aberrantes ou anomalies. Vous remarquerez dans la figure ci-dessus que l’algorithme a déterminé 3 clusters principaux : le bleu, le vert et le jaune. Les points colorés en violet constituent des anomalies détectées par le DBSCAN. Évidemment suivant la valeur de ε et le nombre de voisins minimal le partitionnement peut varier.
Notion de distance et choix du ε
Dans cet algorithme deux points sont clés :
Quelle est la métrique utilisée pour évaluer la distance entre une observation et ses voisins ? quel est le ε idéal ?
Dans le DBSCAN on utilise généralement la distance euclidienne, soient p = (p1,….,pn) et q = (q1,….,qn) :
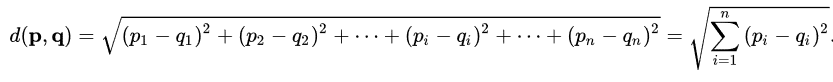
À chaque observation, pour compter le nombre de voisins à au plus une distance ε , on calcule la distance euclidienne entre le voisin et l’observation et vérifie si c’est inférieur à ε.
Reste maintenant à savoir comment choisir le bon epsilon. Supposons que dans notre exemple nous choisissons de tester l’algorithme avec des valeurs différentes de ε . Voici le résultat :
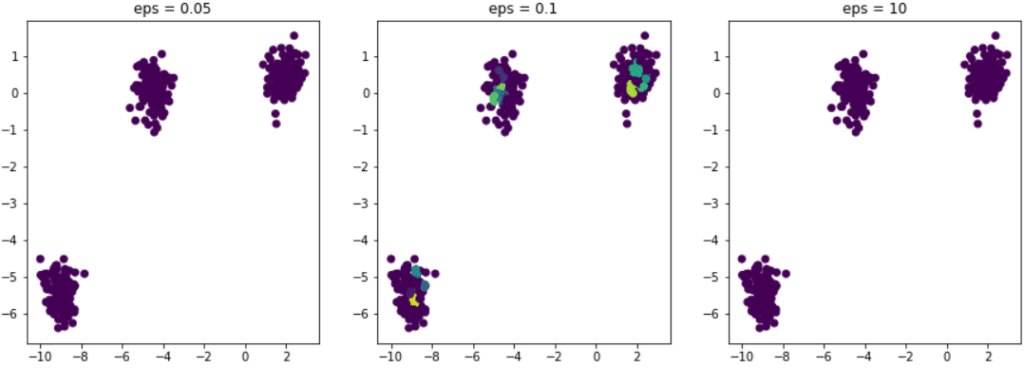
Dans les trois exemples le nombre de voisins minimal est toujours fixé à 5.
Si ε est trop petit le ε-voisinage est trop faible et toutes les observations du jeu de données sont considérées comme des anomalies.
C’est le cas de la figure de gauche eps = 0.05.
A contrario si epsilon est trop grand chaque observation contient dans son ε-voisinage toutes les autres observations du jeu de données. Par conséquent nous n’obtenons qu’un unique cluster. Il est donc très important de bien calibrer le ε pour obtenir un partitionnement de qualité.
Une méthode simple pour optimiser le ε consiste à regarder pour chaque observation à quelle distance se situe son voisin le plus proche. Ensuite il suffit de fixer un ε tel qu’une part « suffisamment grande » des observations aient une distance à son plus proche voisin inférieure à ε. Par « suffisamment grande » on entend 90-95% des observations qui doivent avoir au moins un voisin dans leur ε-voisinage.
Comment implémenter le DBSCAN avec Python ?
L’entraînement du DBSCAN est facilité avec la librairie Scikit-Learn. Notre jeu de données qui a servi d’exemple se crée facilement avec la fonctionalité make_blobs de Scikit-Learn. Voici comment l’implémenter en code :
Maintenant que nous avons notre jeu de données nous allons chercher à déterminer le ε optimal pour obtenir un meilleur partitionnement de notre jeu de données.
Scikit-Learn met à disposition une classe NearestNeighbors qui permet de déterminer les voisins les plus proches de chaque observation ainsi que les distances. Voici comment l’implémenter en code :
Voici le résultat obtenu :
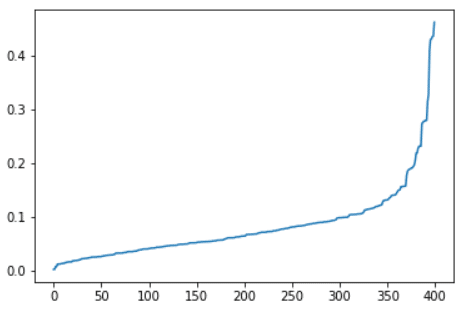
Comme nous l’avons vu précédemment nous allons choisir un ε de tel sorte que 90% des observations aient une distance au proche voisin inférieure à ε. Dans notre exemple 0.2 semble convenir.
Maintenant que nous avons optimisé notre ε nous pouvons effectuer notre partitionnement en utilisant DBSCAN qui est déjà implémenté dans Scikit-Learn.
Voici le résultat obtenu :

Les arguments eps et min_samples permettent de fixer les paramètres de l’algorithme à savoir la distance ε et le nombre minimal de voisins pour être considéré comme une observation cœur.
L’algorithme a donc détecté 3 principaux clusters et quelques anomalies. Chacune des observations est étiquetée avec l’étiquette du cluster correspondant (par exemple 0,1,2). Les anomalies sont étiquetées en -1 et forment donc une classe à part en plus des 3 clusters détectés.
L’utilisation d’un algorithme de clustering tel que le DBSCAN n’est pas aisée suivant les données dont vous disposez. Il faudra souvent les retravailler.
Cette série sur le Clustering vous a plu ? Les formations DataScientest vous apprendrons à maîtriser tous les principaux algorithmes de clustering ainsi qu’à les interpréter sur des jeux de données.
Découvrez les prochaines dates de lancement rapidement !









