Réaffirmant l’importance de la loi normale, le théorème central limite figure parmi les concepts incontournables des statistiques. Mais alors de quoi s’agit-il exactement ? Comment se traduit-il ? Et surtout, comment s’applique-t-il ? C’est ce que nous allons voir dans cet article.
Le théorème central limite et la convergence vers la loi normale
Le théorème central limite établit la convergence d’une suite de variables définies sur le même espace vers une loi normale centrée réduite. Autrement dit : plus on additionne de variables aléatoires indépendantes et identiquement distribuées, plus la distribution de probabilité de la nouvelle variable sera proche d’une distribution normale (également appelé courbe gaussienne ou une courbe en cloche). Et cela vaut pour tout type de distributions de probabilité d’un événement aléatoire, comme la distribution uniforme continue, la distribution triangulaire, la distribution exponentielle, etc.
Dès lors que cet événement est répété suffisamment souvent, sa moyenne converge progressivement vers une distribution normale. Même si au début (après avoir additionné les variables une ou deux fois), la distribution n’avait rien de normal, elle le devient progressivement à mesure que l’addition des variables augmente.
C’est justement ce principe qui permet aux statisticiens d’affirmer que la loi normale est la loi des phénomènes naturels.
Un peu d’histoire : Le théorème central limite a commencé à voir le jour dès 1718 grâce à De Moivre qui a démontré l’importance de la loi normale. Mais c’est véritablement avec les travaux de Pierre-Simon de Laplace en 1812 que ce théorème est véritablement appliqué pour des cas particuliers. Il faudra ensuite 1920 et l’ouvrage de George Pólya (« Sur le théorème central du calcul probabiliste, parmi ceux ayant rapport à la notion de limite, et le problème des moments ») pour lui donner le nom de Théorème central limite.
L’application mathématique du théorème de la limite centrale
- X1, X2, … : comme une suite de variables aléatoires réelles indépendantes et identiquement distribuées.
- σ ≠ 0 : l’espérance μ et l’écart-type σ de la loi D ne sont pas infinis.
- Sn = X1+X2+X3 … : comme la somme de toutes les variables aléatoires.
- nμ : correspond à l’espérance de Sn
- σ√n: correspond à l’écart-type de Sn
Le théorème central limite stipule :
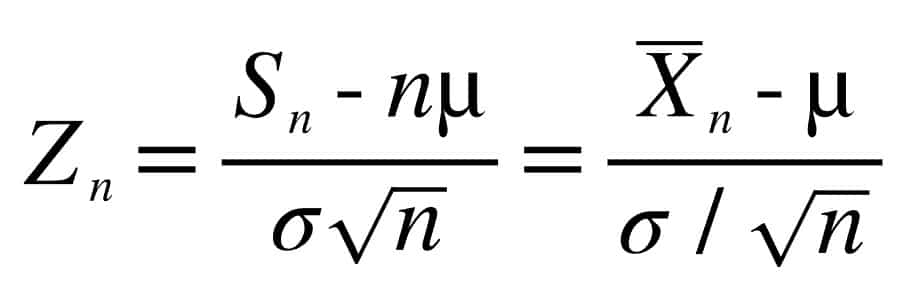
Ici, l’espérance de Znvaut 0 et son écart-type vaut 1. Autrement dit, la variable est centrée et réduite.
Zntend donc vers la loi normale centrée réduite lorsque ntend vers l’infini.
Ainsi pour tout réel z :
lim n→∞ P (Zn ≤ z) = Φ(z)
où : Φ est la fonction de répartition de Ν(0,1)
Exemple d’application du théorème central limite
Pour vous aider à mieux comprendre le théorème de la limite centrale, voici un exemple concret.
Marine et Julien jouent aux dés. À chaque fois qu’ils tombent sur pair, ils gagnent 1 €, et à chaque fois qu’ils tombent sur impair, ils perdent 1 €. Dans ce cas, les nombres pairs et impairs sont des variables aléatoires identiquement distribuées, puisque Marine et Julien ont autant de chance de gagner que de perdre. Au cours des premières parties, il se peut que la balance penche davantage du côté des nombres pairs (et donc des gains) ou des nombres impairs (et donc des pertes). Mais au fur et à mesure qu’ils jouent, leur probabilité de gain ou de perte est proche de 0.
Ce théorème central limite se retrouve dans de nombreux cas de la vie courante. Par exemple, la taille et le poids des individus au sein d’une population, la distribution des salaires au sein d’une entreprise, … La moyenne de ces résultats finit toujours par ressembler à une courbe en cloche à mesure qu’on élargit l’échantillon de la population,
Du fait de la grande variété de ces applications, le théorème central limite est un outil statistique incontournable pour les data scientists, puisqu’il leur permet de modéliser des modèles de Machine Learning. En plus des outils de science des données, il convient donc de maîtriser les concepts mathématiques. C’est justement pour cette raison qu’une formation s’avère indispensable. Découvrez nos programmes.
Ce qu’il faut retenir
- Les variables aléatoires identiquement distribuées suivent une loi normale à mesure qu’elles sont additionnées.
- De par cette affirmation, le théorème central limite souligne l’importance de la loi normale.
- D’ailleurs, ce théorème s’applique pour une grande variété d’hypothèses ; depuis un jeu de hasard, jusqu’à la détermination du salaire moyen ou la taille de la population.