On dit qu’un modèle possède la propriété de Markov si son état à un instant T dépend uniquement de son état à l’instant T-1. Si on peut observer les états dans lesquels se trouve le modèle à chaque instant, on parle de modèle de Markov observable. Sinon, on parle de modèle de Markov caché. Dans cet article, nous allons illustrer ces modèles pour comprendre leur fonctionnement et leur utilité.
Définition mathématique rigoureuse
Mathématiquement, une suite de variables aléatoires (Xn) à valeurs dans un espace d’états E est une chaîne de Markov si elle vérifie la propriété de Markov faible. Cette propriété s’exprime par la relation suivante :
P(Xn+1 = in+1 | X1 = i1, …, Xn = in) = P(Xn+1 = in+1 | Xn = in)
Cette équation signifie que la probabilité de transition vers l’état futur i_{n+1} ne dépend que de l’état présent i_n, et non de la séquence complète des états passés.
Les éléments clés d'une chaîne de Markov
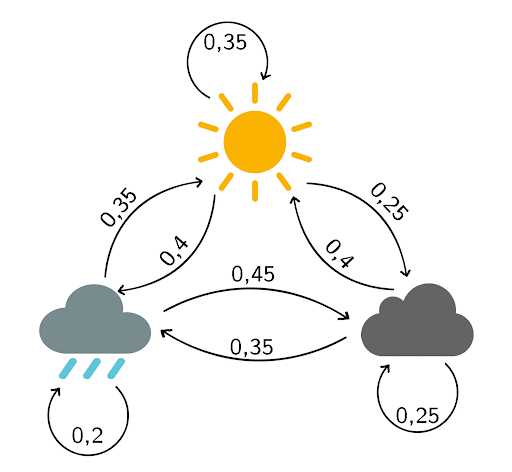
L’espace des états E : l’ensemble de tous les états possibles dans lesquels le système peut se trouver. Dans notre exemple météorologique, E = {soleil, nuages, pluie}.
Les probabilités de transition : P(X_{n+1} = j | X_n = i) représente la probabilité de passer de l’état i à l’état j en une étape.
L’homogénéité temporelle : si ces probabilités de transition ne dépendent pas du temps n, on dit que la chaîne est homogène. C’est le cas le plus fréquemment étudié.
Cette formalisation mathématique permet de distinguer clairement les chaînes de Markov des autres processus stochastiques et constitue la base de toute leur théorie.
Histoire et fondements des chaînes de Markov

Les chaînes de Markov tirent leur nom du mathématicien russe Andreï Andreïevitch Markov (1856-1922), qui introduisit ce concept en 1902 dans le cadre de ses recherches sur l’extension de la loi des grands nombres aux quantités dépendantes.
Markov s’intéressait initialement à étendre les théorèmes limites des probabilités au-delà du cas des variables aléatoires indépendantes. Sa motivation était de comprendre comment la loi des grands nombres pouvait s’appliquer à des séquences d’événements où chaque événement dépend de celui qui le précède, mais pas de l’ensemble de l’historique.
L'innovation conceptuelle
L’idée révolutionnaire de Markov était de modéliser des processus où le futur ne dépend du passé qu’à travers le présent. Cette propriété, aujourd’hui appelée « propriété de Markov », peut s’exprimer intuitivement ainsi : « l’histoire n’importe que par son influence sur l’état actuel ».
Markov lui-même appliqua ses chaînes à l’analyse des successions de lettres dans la littérature russe, notamment dans l’œuvre « Eugène Onéguine » de Pouchkine, démontrant ainsi que les concepts mathématiques pouvaient s’appliquer à des domaines non-mathématiques.
Développements modernes
Depuis leur création, les chaînes de Markov ont connu un développement extraordinaire et sont devenues un outil fondamental dans de nombreux domaines scientifiques et technologiques, de la physique statistique à l’intelligence artificielle moderne.
Modèle de Markov observable

Considérons la situation qui suit :
Vous êtes enfermés chez vous un jour de pluie, et vous aimeriez déterminer le temps qu’il fera lors des cinq prochains jours.
Comme vous n’êtes pas météorologue, vous vous simplifiez la tâche en faisant l’hypothèse que la météo suit un modèle de Markov: le temps qu’il fait au jour J dépend uniquement du temps qu’il fait au jour J-1.
Pour simplifier encore plus, vous considérez qu’il y a seulement trois temps possibles: soleil, nuages ou pluie.
En se basant sur les observations des derniers mois, vous établissez le diagramme de transitions suivant :
La matrice de transition associée est
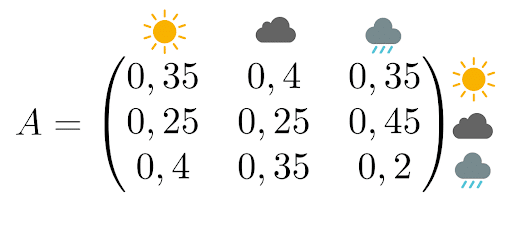
Pour rappel, cette matrice se lit de cette manière :
- La probabilité qu’il fasse beau demain sachant qu’il pleut aujourd’hui est de 35%
- La probabilité qu’il y ait des nuages demain sachant qu’il y en a déjà aujourd’hui est de 25%
Calculons la probabilité que le temps des cinq prochains jours soit “soleil, soleil, pluie, nuages, soleil”.
Comme le temps d’un jour dépend uniquement du temps qu’il a fait la veille, il suffit de multiplier les probabilités (pour rappel il pleut aujourd’hui):
P(Soleil, Soleil, Pluie, Nuages, Soleil | Pluie) = P(Soleil | Pluie) P(Soleil | Soleil) P(Pluie | Soleil) P(Nuages | Pluie) P(Soleil | Nuages)
P(Soleil, Soleil, Pluie, Nuages, Soleil | Pluie) = 0,35 × 0,35 × 0,4 × 0,45 × 0,4
P(Soleil, Soleil, Pluie, Nuages, Soleil | Pluie) = 0,0088
On peut calculer cette probabilité pour toutes les combinaisons possibles, et sélectionner la combinaison avec la probabilité la plus grande pour répondre à la problématique.
Dans notre cas, voici les 5 combinaisons qui ont le plus de chance d’être réalisées :
| J+1 | J+2 | J+3 | J+4 | J+5 | Probabilité (%) |
|---|---|---|---|---|---|
| Nuages | Soleil | Pluie | Nuages | Soleil | 1.30 |
| Nuages | Soleil | Pluie | Nuages | Pluie | 1.13 |
| Nuages | Soleil | Soleil | Pluie | Nuages | 1.13 |
| Nuages | Pluie | Nuages | Soleil | Pluie | 1.13 |
| Nuages | Pluie | Nuages | Pluie | Nuages | 1.12</ |
Propriétés fondamentales de la matrice de transition

La matrice de transition que nous avons utilisée dans l’exemple précédent possède des propriétés mathématiques importantes qu’il convient de comprendre.
Structure de la matrice
Une matrice de transition P = (p_{ij}) doit respecter deux contraintes essentielles :
- Tous les éléments sont positifs ou nuls : p_{ij} ≥ 0 pour tout i,j
- Chaque ligne somme à 1 : Σ_j p_{ij} = 1 pour tout i
Cette seconde propriété reflète le fait que depuis n’importe quel état, le système doit nécessairement transiter vers un état (y compris rester dans le même état).
Puissances de la matrice et prédictions à long terme
L’une des propriétés les plus remarquables est que la matrice P^n (P élevée à la puissance n) donne directement les probabilités de transition en n étapes. Ainsi, l’élément (P^n)_{ij} représente la probabilité de passer de l’état i à l’état j en exactement n étapes.
Cette propriété nous permet de faire des prédictions météorologiques à long terme. Par exemple, si nous calculons P10, nous obtenons les probabilités de transition sur 10 jours.
Convergence vers l'équilibre
Sous certaines conditions, les puissances successives de la matrice P convergent vers une matrice limite, dont toutes les lignes sont identiques. Cette ligne commune représente la distribution stationnaire du système ; la répartition des probabilités vers laquelle le système tend à long terme, indépendamment de son état initial.
Dans notre exemple météorologique, cela signifierait qu’à très long terme, la probabilité d’avoir du soleil, des nuages ou de la pluie devient constante et prévisible.
Classification des états dans une chaîne de Markov

Une fois la matrice de transition établie, il est essentiel de comprendre le comportement à long terme de chaque état. Cette analyse permet de classifier les états selon leurs propriétés dynamiques.
États transitoires et récurrents
Un état est dit transitoire si, en partant de cet état, il existe une probabilité non nulle de ne jamais y revenir. À l’inverse, un état est récurrent si, en partant de cet état, on est certain d’y revenir tôt ou tard.
Dans notre exemple météorologique, si nous modifions la matrice pour inclure un état « tempête » dont on ne peut sortir que vers « pluie » et où l’on ne peut plus revenir, alors « tempête » serait un état transitoire.
États absorbants
Un état est dit absorbant s’il est impossible d’en sortir une fois qu’on y est entré. Mathématiquement, cela signifie que p_{ii} = 1 pour cet état i.
Exemple concret : dans un modèle de durée de vie d’un organisme avec les états « juvénile », « adulte », « sénescent », et « décédé », l’état « décédé » est absorbant car un organisme mort ne peut changer d’état.
Chaînes irréductibles
Une chaîne de Markov est irréductible si tous les états communiquent entre eux, c’est-à-dire qu’il est possible de passer de n’importe quel état à n’importe quel autre état en un nombre fini d’étapes.
Notre modèle météorologique est irréductible : on peut passer du soleil à la pluie (via les nuages), de la pluie au soleil, etc. Cette propriété garantit l’existence d’une distribution stationnaire unique.
Périodicité
Un état a une période d si on ne peut y revenir qu’à des instants multiples de d. Si d = 1, l’état est dit apériodique. Une chaîne irréductible et apériodique converge toujours vers sa distribution stationnaire.
Cette classification permet de prédire le comportement asymptotique du système et détermine quels outils mathématiques peuvent être appliqués pour l’analyse.
Distribution stationnaire et convergence vers l'équilibre

Nous avons évoqué précédemment le concept de convergence vers l’équilibre. Approfondissons maintenant cette notion fondamentale.
Qu'est-ce qu'une distribution stationnaire ?
Une distribution stationnaire π est un vecteur de probabilités qui reste inchangé par la dynamique de la chaîne. Mathématiquement, elle vérifie l’équation : π = πP, où P est la matrice de transition.
Dans notre exemple météorologique, si la distribution stationnaire est π = (0.4, 0.3, 0.3) pour (soleil, nuages, pluie), cela signifie qu’à long terme, il y aura du soleil 40% du temps, des nuages 30% du temps, et de la pluie 30% du temps, indépendamment de la météo d’aujourd’hui.
Existence et unicité
Pour une chaîne de Markov irréductible sur un espace d’états fini, il existe toujours une unique distribution stationnaire. Cette propriété remarquable garantit que le système a un comportement prévisible à long terme.
Le théorème ergodique
Le théorème ergodique est l’un des résultats les plus puissants de la théorie des chaînes de Markov. Il établit que, pour une chaîne irréductible et apériodique :
- Convergence : Peu importe l’état initial, les probabilités convergent vers la distribution stationnaire
- Loi forte des grands nombres : La proportion de temps passé dans chaque état converge vers sa probabilité stationnaire
Concrètement, cela signifie que si nous observons notre météo pendant de nombreuses années, la fréquence observée de chaque type de temps convergera vers les probabilités de la distribution stationnaire.
Applications pratiques de l'ergodicité
Cette propriété permet de calculer des moyennes à long terme sans simulation exhaustive. Par exemple, si une machine a une probabilité stationnaire de 0.95 d’être fonctionnelle, nous savons qu’elle sera disponible 95% du temps sur le long terme, information cruciale pour la planification industrielle.
L’ergodicité justifie également l’utilisation des chaînes de Markov dans les algorithmes d’échantillonnage Monte-Carlo : en laissant la chaîne évoluer suffisamment longtemps, on obtient des échantillons selon la distribution souhaitée.
Exercices pratiques pour maîtriser les chaînes de Markov

Pour consolider votre compréhension, voici quelques exercices classiques avec leurs solutions détaillées.
Exercice 1 : L'urne d'Ehrenfest
Une urne contient 4 boules numérotées. À chaque étape, on tire un numéro au hasard et on déplace la boule correspondante vers l’autre urne. L’état du système est le nombre de boules dans la première urne.
Question : Déterminez la matrice de transition et calculez la distribution stationnaire.
Solution : Les états possibles sont {0,1,2,3,4}. Si l’urne 1 contient i boules, la probabilité de passer à l’état i-1 est i/4 (tirer une boule de l’urne 1), et la probabilité de passer à l’état i+1 est (4-i)/4 (tirer une boule de l’urne 2).
La distribution stationnaire suit une loi binomiale : π(i) = C(4,i)/16, soit π = (1/16, 4/16, 6/16, 4/16, 1/16).
Exercice 2 : Marche aléatoire sur un graphe
Un pion se déplace sur un carré dont les sommets sont A, B, C, D. À chaque étape, il passe à un sommet adjacent avec probabilité égale.
Question : La chaîne est-elle irréductible ? Périodique ? Calculez le temps de retour moyen.
Solution :
- Irréductible : Oui, on peut aller de tout sommet vers tout autre
- Périodique : Oui, de période 2 (il faut un nombre pair d’étapes pour revenir au point de départ)
- Temps de retour moyen : 4 étapes pour chaque sommet
Exercice 3 : Modèle de durée de vie
Un organisme passe par les états : juvénile (J), mature (M), sénescent (S), décédé (D). La matrice de transition est :
J M S D
J [0.6 0.4 0 0 ]
M [0 0.7 0.3 0 ]
S [0 0 0.8 0.2]
D [0 0 0 1 ]
Question : Calculez la probabilité qu’un individu juvénile atteigne l’état sénescent.
Solution : Il faut résoudre le système d’équations. La probabilité cherchée est de 0.4 × (0.3/0.3) = 0.4, car tout individu mature atteint forcément l’état sénescent.
Exercice 4 : Temps d'absorption
Reprenons l’exercice précédent. Calculez l’espérance de vie d’un individu juvénile.
Solution : En utilisant les équations de temps d’absorption, l’espérance de vie d’un juvénile est de 8.33 unités de temps environ.
Ces exercices illustrent les concepts théoriques à travers des situations concrètes et vous préparent à modéliser vos propres problèmes avec les chaînes de Markov.
Extension aux chaînes de Markov à temps continu

Jusqu’à présent, nous avons étudié des chaînes de Markov à temps discret, où les transitions se produisent à des instants réguliers (jour 1, jour 2, etc.). Dans de nombreuses applications réelles, les changements d’état peuvent survenir à tout moment : c’est le domaine des processus de Markov à temps continu.
Différences conceptuelles fondamentales
Au lieu de matrices de transition, nous utilisons des générateurs infinitésimaux qui décrivent les taux de transition instantanés. Si q_{ij} représente le taux de transition de l’état i vers l’état j, alors la probabilité de transition pendant un petit intervalle dt est approximativement q_{ij} × dt.
Exemple concret : centre d'appels
Considérons un centre d’appels où les appels arrivent selon un processus de Poisson avec un taux λ = 5 appels/heure, et chaque appel est traité en moyenne en 10 minutes (taux de service μ = 6 appels/heure).
Les états représentent le nombre d’appels en cours de traitement. Les transitions sont :
- État n → État n+1 avec taux λ (arrivée d’un appel)
- État n → État n-1 avec taux nμ (fin de traitement d’un appel)
Équations de Chapman-Kolmogorov continues
La dynamique du système est gouvernée par l’équation différentielle : dP(t)/dt = P(t) × Q
où Q est la matrice générateur et P(t) donne les probabilités de transition au temps t.
Distribution stationnaire en temps continu
À l’équilibre, la condition devient : π × Q = 0, où π est la distribution stationnaire. Cette équation exprime l’équilibre des flux : pour chaque état, le taux d’entrée égale le taux de sortie.
Applications pratiques
- Fiabilité des systèmes : Un équipement peut tomber en panne à tout moment (taux λ) et être réparé (taux μ). Le processus continu modélise naturellement ces événements imprévisibles.
- Épidémiologie : Les modèles SIR (Susceptible-Infecté-Rétabli) utilisent des taux de contamination et de guérison continus pour prédire l’évolution des épidémies.
- Finance quantitative : Les changements de prix d’actifs financiers suivent des processus continus, modélisés par des diffusions (extensions stochastiques des processus de Markov).
Avantages du temps continu
Cette approche capture plus fidèlement la réalité de nombreux phénomènes naturels et permet des calculs analytiques souvent plus élégants. Elle constitue également le pont vers des modèles plus sophistiqués comme les processus de diffusion et les équations différentielles stochastiques.
Méthodes de Monte-Carlo par chaînes de Markov (MCMC)

Les chaînes de Markov trouvent une application révolutionnaire dans les méthodes d’échantillonnage statistique, particulièrement quand les distributions sont trop complexes pour être échantillonnées directement.
Le principe fondamental du MCMC
L’idée géniale consiste à construire une chaîne de Markov dont la distribution stationnaire est précisément la distribution que nous souhaitons échantillonner. En laissant évoluer cette chaîne suffisamment longtemps, les échantillons obtenus suivront approximativement la distribution cible.
L'algorithme de Metropolis-Hastings
Cet algorithme universel permet d’échantillonner n’importe quelle distribution π(x), même si on ne connaît cette fonction qu’à une constante de normalisation près.
Principe de fonctionnement :
- À partir de l’état actuel x_t, proposer un nouvel état y selon une distribution de proposition q(y|x_t)
- Calculer le ratio d’acceptation : α = min(1, [π(y)q(x_t|y)] / [π(x_t)q(y|x_t)])
- Accepter y avec probabilité α, sinon rester en x_t
Cette procédure garantit que la distribution stationnaire de la chaîne résultante est exactement π(x).
Applications en statistique bayésienne
En inférence bayésienne, nous cherchons souvent à échantillonner la distribution a posteriori des paramètres. Si nous avons des données D et des paramètres θ avec une prior π(θ), la distribution a posteriori est :
π(θ|D) ∝ π(D|θ) × π(θ)
Le MCMC permet d’échantillonner cette distribution même quand elle n’a pas de forme analytique simple, révolutionnant ainsi l’analyse statistique moderne.
L'échantillonnage de Gibbs
Cas particulier du Metropolis-Hastings pour les distributions multivariées. Au lieu de mettre à jour tous les paramètres simultanément, on met à jour chaque paramètre individuellement en conditionnant sur les autres.
Cette méthode est particulièrement efficace pour les modèles graphiques comme les réseaux bayésiens, où les distributions conditionnelles ont souvent des formes simples.
Diagnostic de convergence
Un défi majeur du MCMC est de déterminer quand la chaîne a « oublié » son état initial et échantillonne la vraie distribution stationnaire. Les diagnostics incluent :
- Visualisation des traces temporelles
- Critère de Gelman-Rubin (comparaison de chaînes multiples)
- Tests d’autocorrélation
Applications contemporaines
- Intelligence artificielle : Les réseaux de neurones bayésiens utilisent MCMC pour quantifier l’incertitude des prédictions, crucial pour les applications critiques.
- Épidémiologie computationnelle : Les modèles de propagation d’épidémies avec paramètres incertains sont calibrés par MCMC sur les données observées.
- Finance quantitative : L’estimation de modèles de volatility stochastique et la valorisation d’options complexes s’appuient massivement sur les méthodes MCMC.
Le MCMC illustre parfaitement comment un concept mathématique fondamental (les chaînes de Markov) devient un outil computationnel révolutionnaire pour la science des données moderne.
Chaînes de Markov dans l'écosystème de la data science moderne

À l’ère du big data et de l’intelligence artificielle, les chaînes de Markov ont trouvé de nouveaux domaines d’application qui dépassent largement leur cadre théorique initial.
Traitement automatique du langage naturel (NLP)
Les modèles de langue basés sur les chaînes de Markov constituent les précurseurs des architectures modernes comme GPT. Ils modélisent la probabilité d’apparition d’un mot en fonction des mots précédents, permettant :
- Génération automatique de texte : En enchaînant les probabilités de transition, on peut générer des phrases cohérentes
- Correction orthographique : Les chaînes de Markov détectent les séquences de caractères improbables
- Classification de textes : Chaque classe (spam/non-spam) a son propre modèle markovien de génération
Systèmes de recommandation
Les plateformes comme Netflix ou Spotify utilisent des chaînes de Markov pour modéliser les parcours utilisateurs :
- États : les contenus consultés
- Transitions : les probabilités de passer d’un contenu à un autre
- Objectif : prédire le prochain contenu susceptible d’intéresser l’utilisateur
Analyse de séquences temporelles en IoT
Dans l’Internet des Objets, les capteurs génèrent des flux de données séquentielles. Les chaînes de Markov permettent :
- Détection d’anomalies : identifier des séquences de mesures inhabituelles
- Maintenance prédictive : anticiper les pannes d’équipements industriels
- Optimisation énergétique : modéliser les patterns de consommation
Cybersécurité et détection de fraudes
Les analystes sécurité utilisent les chaînes de Markov pour :
- Détection d’intrusions : modéliser les comportements normaux d’utilisateurs et identifier les déviations
- Analyse de malwares : les séquences d’appels système révèlent les signatures de logiciels malveillants
- Authentification comportementale : reconnaître les utilisateurs par leurs patterns de navigation
Marketing digital et web analytics
Les chaînes de Markov optimisent l’expérience utilisateur web :
- Analyse de parcours clients : comprendre les chemins de conversion sur un site e-commerce
- A/B testing séquentiel : analyser l’impact des modifications sur les comportements de navigation
- Attribution marketing : mesurer l’efficacité des différents canaux d’acquisition
Bioinformatique computationnelle
Au-delà de l’analyse d’ADN classique, les applications modernes incluent :
- Analyse d’expression génique : modéliser l’évolution temporelle de l’activité des gènes
- Épidémiologie génomique : tracer la propagation de variants viraux par analyse de séquences
- Médecine personnalisée : prédire l’évolution de pathologies à partir de biomarqueurs séquentiels
Intégration avec l'apprentissage automatique
Les chaînes de Markov s’hybrident avec les techniques modernes :
- Feature engineering : créer des variables explicatives à partir de séquences temporelles
- Reinforcement learning : les processus de décision markoviens sous-tendent l’apprentissage par renforcement
- Réseaux de neurones récurrents : les LSTM et GRU généralisent les chaînes de Markov avec de la mémoire adaptative
Ces applications démontrent que les chaînes de Markov, loin d’être un concept purement académique, constituent un pilier méthodologique essentiel pour extraire de la valeur des données séquentielles dans l’économie numérique moderne.
Modèle de Markov caché

On garde les mêmes hypothèses que dans la partie précédente.
Supposons maintenant qu’un psychopathe de la météo vous a enfermé dans une pièce sans fenêtre avec seulement un ordinateur et une lampe. Chaque jour, la lampe s’allume d’une certaine couleur en fonction de la météo. Votre kidnappeur vous fournit la matrice d’observation suivante :
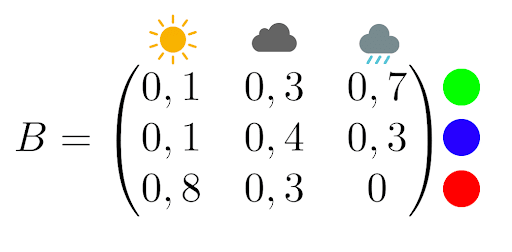
Par exemple s’il pleut, la lampe a 70% de chances d’être verte et 30% de chances d’être bleue.
Vous pourrez rentrer chez vous si vous déterminez le temps qu’il fera lors des cinq prochains jours uniquement en vous basant sur la couleur de la lampe. Vous construisez alors un modèle de Markov caché.
Vous restez enfermé 5 jours et vous relevez les couleurs suivantes:
bleu, bleu, rouge, vert, rouge.
Vous vous souvenez qu’il pleuvait le jour précédant votre enfermement
Vous pouvez alors rédiger un code python qui renvoie la combinaison qui a la plus forte probabilité d’être réalisée :
| J+1 | J+2 | J+3 | J+4 | J+5 | Probabilité (%) |
|---|---|---|---|---|---|
| Nuages | Nuages | Soleil | Pluie | Soleil | 0.045158 |
| Nuages | Pluie | Soleil | Pluie | Soleil | 0.041489 |
| Pluie | Nuages | Soleil | Pluie | Soleil | 0.027095 |
| Nuages | Nuages | Soleil | Pluie | Nuages | 0.021773 |
| Nuages | Pluie | Soleil | Pluie | Nuages | 0.020004 |
NB : On aurait également pu implémenter l’algorithme de Viterbi, qui aurait renvoyé la combinaison la plus probable, soit [‘Nuages’, ‘Nuages’, ‘Soleil’, ‘Pluie’, ‘Soleil’].
Cette approche de prédiction est intéressante mais très sommaire. Si vous voulez apprendre à faire des prédictions plus impressionnantes, avec des algorithmes de machine learning par exemple, contactez-nous directement en ligne pour avoir plus d’informations sur nos formations en data science !
Approfondissement des modèles de Markov cachés (HMM)

Notre exemple du « psychopathe météorologique » introduit les HMM de manière ludique, mais ces modèles méritent un développement plus technique car ils constituent l’un des outils les plus puissants de l’apprentissage statistique.
Structure mathématique d'un HMM
Un modèle de Markov caché se compose de trois éléments essentiels :
- Les états cachés : la séquence d’états non observables (ici, la météo réelle)
- Les observations : ce que nous pouvons mesurer (ici, la couleur de la lampe)
- Deux matrices de probabilités : la matrice de transition entre états cachés A, et la matrice d’émission/observation B
Les trois problèmes fondamentaux des HMM
La théorie des HMM s’articule autour de trois questions cruciales :
Problème 1 : Évaluation Quelle est la probabilité d’observer une séquence donnée ? L’algorithme Forward calcule efficacement cette probabilité en évitant l’explosion combinatoire.
Problème 2 : Décodage Quelle est la séquence d’états cachés la plus probable ? L’algorithme de Viterbi résout ce problème par programmation dynamique. Dans notre exemple météo, il détermine la séquence de temps la plus vraisemblable given les couleurs observées.
Problème 3 : Apprentissage Comment estimer les paramètres du modèle à partir des observations ? L’algorithme de Baum-Welch (variante de l’algorithme EM) optimise itérativement les matrices A et B.
Applications avancées des HMM
- Reconnaissance vocale automatique : Les phonèmes sont les états cachés, les spectrogrammes audio sont les observations. Les HMM modélisent comment chaque phonème génère des caractéristiques acoustiques spécifiques.
- Analyse de séquences biologiques : En bioinformatique, les HMM identifient les gènes dans l’ADN : les régions codantes/non-codantes sont les états cachés, les nucléotides (A,T,G,C) sont les observations.
- Finance quantitative : Les régimes de marché (haussier/baissier) sont cachés, les rendements d’actifs sont observés. Les HMM détectent les changements de régime pour ajuster les stratégies d’investissement.
Limites et extensions
Les HMM classiques supposent l’indépendance des observations conditionnellement aux états. Les HMM hiérarchiques et les réseaux de neurones récurrents lèvent cette limitation pour des modélisations plus sophistiquées.
Applications concrètes des chaînes de Markov

Au-delà de la prédiction météorologique, les chaînes de Markov trouvent des applications dans de nombreux domaines concrets :
PageRank et moteurs de recherche
L’algorithme PageRank de Google utilise une chaîne de Markov pour classer l’importance des pages web. Chaque page web est un état, et les liens entre pages définissent les probabilités de transition. L’importance d’une page correspond à sa probabilité dans la distribution stationnaire de cette chaîne.
Secteur financier et assurance
Les compagnies d’assurance automobile utilisent les chaînes de Markov pour leurs systèmes de bonus-malus. L’état représente la classe de bonus du conducteur, et les transitions dépendent du nombre d’accidents déclarés chaque année. Cette modélisation permet de calculer les primes d’assurance de manière actuarielle.
Bioinformatique et génétique
En analyse de séquences ADN, les chaînes de Markov modélisent les relations entre nucléotides successifs (A, T, G, C). Les modèles markoviens cachés (HMM) sont particulièrement utiles pour identifier des gènes, prédire la structure des protéines, ou détecter des régions codantes dans le génome.
Fiabilité industrielle
Dans l’industrie, les chaînes de Markov modélisent les systèmes techniques avec des états comme « fonctionnel », « en panne », « en maintenance ». Cela permet de calculer la disponibilité des équipements, planifier la maintenance préventive, et optimiser les coûts de réparation.
Intelligence artificielle moderne
Les chatbots et systèmes de génération de texte utilisent des chaînes de Markov pour prédire le mot suivant dans une phrase. Les claviers prédictifs de smartphones appliquent ce principe pour suggérer des mots en fonction du contexte de frappe.
Théorie des files d'attente
Les centres d’appels, guichets bancaires, et serveurs informatiques sont modélisés par des chaînes de Markov où les états représentent le nombre de clients en attente. Cela permet d’optimiser le dimensionnement des ressources et réduire les temps d’attente.
Pour aller plus loin : références essentielles

La théorie des chaînes de Markov constitue un domaine mathématique riche avec une littérature académique approfondie. Voici les références incontournables pour approfondir vos connaissances.
Ouvrages de référence fondamentaux
- Norris, J.R. « Markov Chains » (Cambridge University Press, 1997) Considéré comme LA référence moderne pour les chaînes de Markov. Couvre rigoureusement la théorie tout en restant accessible. Indispensable pour une compréhension mathématique solide.
- Sericola, Bruno « Chaînes de Markov – Théorie, algorithmes et applications » (Hermes/Lavoisier, 2013) Ouvrage français de référence, particulièrement apprécié pour ses nombreuses applications pratiques et ses algorithmes détaillés.
- Baldi, Paolo et al. « Martingales et chaînes de Markov. Théorie élémentaire et exercices corrigés » (Hermann, 2001) Excellent pour l’apprentissage avec de nombreux exercices corrigés progressifs.
Spécialisation par domaines d'application
- Méléard, Sylvie « Modèles aléatoires en écologie et évolution » (Springer, 2016) Pour les applications en biologie et écologie, avec des modèles de population utilisant les chaînes de Markov.
- Bremaud, Pierre « Markov chains. Gibbs fields, Monte Carlo simulation, and queues » (Springer, 1998) Reference technique pour les files d’attente et les méthodes de Monte-Carlo par chaînes de Markov.
Articles fondateurs historiques
- Markov, A.A. « Extension of the law of large numbers to dependent quantities » (1906) L’article original qui a introduit le concept. Disponible en traduction dans le Journal Électronique d’Histoire des Probabilités et de la Statistique.
Ressources pédagogiques complémentaires
- Grinstead, Charles M. & Snell, J. Laurie « Introduction to Probability » (AMS) Chapitre excellent sur les chaînes de Markov avec approche très pédagogique et exercices interactifs disponibles en ligne.
- Exercices en ligne L’université de Nice Sophia Antipolis propose des exercices corrigés interactifs via la plateforme WIMS, parfaits pour s’entraîner.
Ressources numériques modernes
- Philippe Gay « Markov et la Belle au bois dormant » (Images des Maths, 2014) Article de vulgarisation excellent qui présente les enjeux modernes des chaînes de Markov de manière accessible.
Ces références vous permettront de progresser de l’initiation aux aspects les plus avancés, selon vos objectifs d’apprentissage et vos domaines d’application privilégiés.